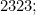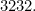December 2007
Imagine picking the four hymn numbers out of a hat. First note that four-hymn combinations with one 1-digit number and three 3-digit numbers come in four types: the one digit number can occur in first, second, third or last place of the selection. So the overall chance of picking such a combination is equal to:
| Chance of picking a combination with 1-digit number in 1st place |
| + chance of picking a combination with 1-digit number in 2nd place |
| + chance of picking a combination with 1-digit number in 3rd place |
| + chance of picking a combination with 1-digit number in 4th place. |
Each of the terms in this sum is equal to
so the overall chance of picking four hymn numbers such that one of them has 1 digit and the others have three digits is
Now for the chance of picking a combination with two 2-digit numbers and two 3-digit numbers. There are 6 ways in which to choose the positions of the two 2-digit numbers within the string of four numbers, so this time the selection comes in 6 different types:
The chance of picking a combination of each individual type is
so the overall chance is
In general, the number of ways you can choose a set of 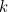 positions within a sequence of length
positions within a sequence of length 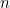 is
is
where
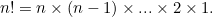
In our examples, we first had
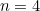
with
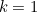
, giving
and then
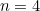
with
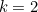
, giving
Return to main article.
![\[ 9/999 \times 900/999 \times 900/999 \times 900/999, \]](/MI/7cbdcdb0d1affd21a57505a8ef4c82e0/images/img-0001.png)
![\[ 9/999 \times (900/999)^3 \times 4 = 0.0263. \]](/MI/7cbdcdb0d1affd21a57505a8ef4c82e0/images/img-0002.png)
![\[ (90/999)^2 \times (900/999)^2, \]](/MI/2ee1d6f4cc1c4369c906521c37bb7257/images/img-0001.png)
![\[ (90/999)^2 \times (900/999)^2 \times 6 = 0.0395$$ \]](/MI/2ee1d6f4cc1c4369c906521c37bb7257/images/img-0002.png)
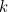 positions within a sequence of length
positions within a sequence of length 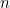 is
is ![\[ \frac{n!}{k!(n-k)!}, \]](/MI/413baf4c56643026822a18e23c6df0fa/images/img-0003.png)
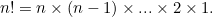 In our examples, we first had
In our examples, we first had 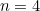 with
with 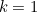 , giving
, giving ![\[ \frac{4!}{1!3!} = 4, \]](/MI/413baf4c56643026822a18e23c6df0fa/images/img-0007.png)
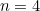 with
with 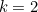 , giving
, giving ![\[ \frac{4!}{2!2!} = 6. \]](/MI/413baf4c56643026822a18e23c6df0fa/images/img-0009.png)