Changing the variables

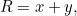
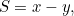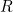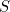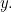We define a new coordinate system $R = x + y,$ $S = x - y,$ in which $R$ and $S$ are tilted at 45 degrees relative to $x$ and $y.$ This gives us

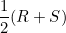	$\displaystyle x$	$\displaystyle =$	$\displaystyle \frac{1}{2}(R+S)$
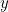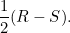	$\displaystyle y$	$\displaystyle =$	$\displaystyle \frac{1}{2}(R-S).$

Substituting this into our expression for the envelope curve

$y(x)=(1-\sqrt {x})^2$

gives

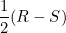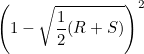$\displaystyle \frac{1}{2}(R-S)$	$\displaystyle =$	$\displaystyle \left(1-\sqrt {\frac{1}{2}(R+S)}\right)^2$
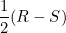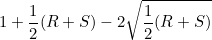$\displaystyle \frac{1}{2}(R-S)$	$\displaystyle =$	$\displaystyle 1+\frac{1}{2}(R+S) - 2\sqrt {\frac{1}{2}(R+S)}$
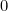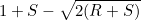$\displaystyle 0$	$\displaystyle =$	$\displaystyle 1+S -\sqrt {2(R+S)}$
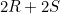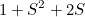$\displaystyle 2R+2S$	$\displaystyle =$	$\displaystyle 1+S^2+2S$
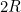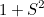$\displaystyle 2R$	$\displaystyle =$	$\displaystyle 1+S^2$
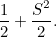$\displaystyle $R $$	$\displaystyle =$	$\displaystyle \frac{1}{2}+\frac{S^2}{2}.$

This is the equation of a parabola.

Login to comment or download PDFs