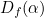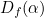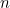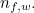
From the graph of $D_f(\alpha)$ we know that there is one minimum. We'll find it by setting the derivative of $D_f(\alpha)$ equal to 0. We have $$D_f(\alpha)=180^\circ+2\alpha-4\beta,$$ where $$\beta=\beta(\alpha)=arcsin{\frac{\sin{\alpha}}{n_{f,w}}.$$ To make things look simpler we'll write $n$ for $n_{f,w}.$ Now $$D_f^\prime(\alpha)=2-4\beta^\prime(\alpha).$$ The derivative of the function 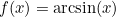$f(x)=\arcsin(x)$ is $$f^\prime(x)=\frac{1}{\sqrt{1-x^2}}.$$ Using the chain rule gives $$\beta^\prime(\alpha)=\frac{\cos{\alpha}}{n\sqrt{1-\frac{\sin^2{\alpha}}{n^2}}}=\frac{\cos{\alpha}}{\sqrt{n^2-\sin^2{\alpha}}}.$$ Thus $$D_f^\prime(\alpha)=2-\frac{4\cos{\alpha}}{\sqrt{n^2-\sin^2{\alpha}}}.$$ Setting $D_f(\alpha)=0$ 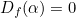gives $$2-\frac{4\cos{\alpha}}{\sqrt{n^2-\sin^2{\alpha}}}=0.$$ Noting that 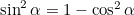$\sin^2{\alpha}=1-\cos^2{\alpha}$ and rearranging gives $$\cos^2{\alpha}=\frac{n^2-1}{3}.$ Thus, $D_f^\prime(\alpha)=0$ for $$\alpha_m=\arccos{\sqrt{\frac{n^2-1}{3}}}.$$

Back to main article