Topography is a branch of geography concerned with the natural and constructed features on the surface of land, such as mountains, lakes, roads, and buildings. Topology is a branch of mathematics concerned with the distortion of shapes. In this, the first of two articles, Ian Short explores topological problems using topography.
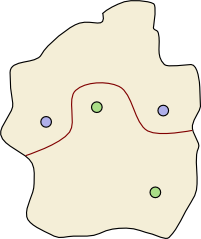
There is a dividing wall separating the blue towns from the green towns.
Dividing walls
There is an island containing four towns — the green tribe live in two of the towns and the blue tribe in the other two. The people from the green towns are enemies of the people from the blue towns, so they decide to build a wall to separate green towns from blue towns. The tribes want to stick together, so the wall must not separate one green town from another, or one blue town from another. The wall must be continuous, it must not intersect itself, it must not split, it must not pass through a town, and each end of the wall must be at the coast. Let us call such a wall a dividing wall.
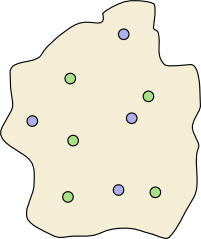
Is there a dividing wall?...
Suppose now that there are more than four blue and green towns. Can we still construct a dividing wall? Each town must be isolated (it must not touch any other town) and it must not lie on the coast. Try to build such a wall yourself using the example to the left, and experiment with other, different, configurations of towns. Can you make a conjecture about when a dividing wall exists?
You may have discovered that dividing walls always exist.
Theorem 1. Given any configuration of blue and green towns, there is a dividing wall that separates blue towns from green towns.
To prove this theorem, let's revisit the previous example, this time with a dividing wall included.
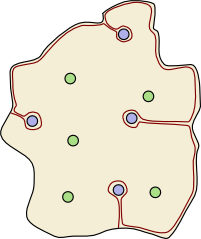
...Yes, there is.
This dividing wall begins at some arbitrary point on the boundary of the island, and works its way clockwise round the island, just slightly inland. Every so often the wall heads along a path inland, performs a quick loop round a blue town, and then heads back to the coast just next to the inland path. Once every blue town has been circled in this fashion the wall terminates at a point on the boundary. The same procedure can be applied with any configuration of towns, and thus we have proved Theorem 1.
(If you find this proof too informal, then see if you can do a better job yourself. Our whole discussion has been informal, so you may wish to work through the material again, fixing definitions and tightening reasoning.)
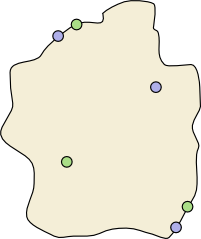
Is there a dividing wall for an island with coastal towns?
Coastal towns
Coastal towns are towns that lie on the boundary of the island — you cannot encircle them by a wall. Is there a dividing wall for the towns on the island to the right? Remember that, as usual, dividing walls cannot touch towns, they separate green from blue, and each end of the wall starts and finishes at the coast.
Is there a dividing wall for every collection of coastal and inland towns? No, there is not. Try to work out the simplest configuration of towns for which a dividing wall does not exist. You will probably come up with the example shown below, which we call the minimal configuration.
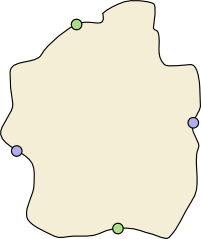
The minimal configuration.
Why is there no dividing wall for this set of towns? Think about where a dividing wall would start and end. By symmetry of the configuration, we can assume that the wall starts in the north-west, between the western blue town and the northern green town. The wall finishes between two of the towns, either in the north-west, north-east, south-east, or south-west. In each case, the dividing wall fails to separate blue from green. Check the four cases yourself. This is the simplest configuration of towns for which there is no dividing wall because, for three towns, there is always a dividing wall, and for four towns configured in a different (topologically different) fashion, there is always a dividing wall.
Can we say precisely when a collection of towns has a dividing wall? Let's call a configuration of towns an alternating configuration if there are four particular coastal towns in the configuration whose colours are, in clockwise order, green blue green blue. In other words, an alternating configuration is one that contains the minimal configuration.
Here is an example of an alternating and a non-alternating configuration of towns:
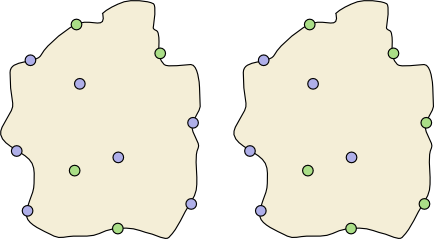
An alternating configuration (left) and a non-alternating configuration (right).
We are now in a position to state our second theorem.
Theorem 2. Alternating configurations of towns do not have a dividing wall, whereas non-alternating configurations of towns do have a dividing wall.
We have already seen that alternating configurations of towns do not have a dividing wall; for if an alternating configuration did have a dividing wall, then that wall would also be a dividing wall for the minimal configuration, which, as we have seen, is impossible. It remains to prove that each non-alternating configuration of towns has a dividing wall. This time we approach the problem as topologists, and our method is illustrated in the following figure:
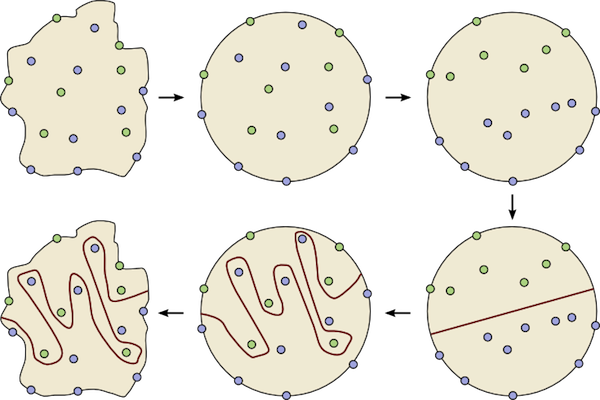
Transforming to the disc and back again.
We begin with the non-alternating configuration of towns shown in the top-left. You may have noticed that the shape of the island is unimportant for dividing walls problems: we can stretch and distort the shape of the island without affecting the existence of dividing walls. So, the first step is to deform our island to a circular shape.
Next, we can distort the interior and boundary of our disc, still without affecting the existence of dividing walls. So in the second step we push all the green towns to one half of the disc and we push the blue towns to the other half (as shown in the top-right of the figure above). It is easy to construct a dividing wall for the resulting collection of towns; we simply choose a diameter of the disc as a wall.
It remains only to unwind the deformations performed in steps one and two; this time we track how the diameter wall is distorted as we unwind. Finally, we end up with a dividing wall for our initial configuration. In this way we see that every non-alternating configuration of towns has a dividing wall, and this concludes the proof of Theorem 2.
Connecting roads
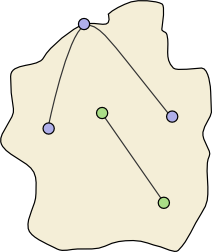
Connecting roads.
History is littered with examples of dividing walls that have contributed to war and misery. Let us suppose that the people from our blue and green towns are more enlightened, although retain their animosity towards each other. Rather than building a wall, they decide to build two roads. One road connects all the blue towns and the other road connects all the green towns. The two roads are not allowed to intersect themselves or each other. The blue road starts at a blue town, and then passes through each of the other blue towns, finishing at another blue town. Likewise for the green road and the green towns. Let us call a pair of such roads connecting roads.
Notice that the connecting road for the blue towns shown on the right passes straight through a coastal town.
We could now return to the start of our study and investigate connecting roads rather than dividing walls. We can bypass these details, however, by stating the next theorem.
Theorem 3. A configuration of towns has a dividing wall if and only if it has a pair of connecting roads.
I have proved enough for one article, so I leave this one with you.
What next?
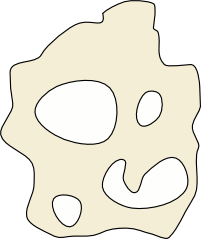
This island has connectivity five.
Our islands so far have pretty basic topography; just a few towns, walls, and roads. What if we add lakes, through which neither walls nor roads can be built? These lakes resemble holes in our shape. In the terminology of topology the number of holes is the connectivity of the shape. We also count the outside of the shape as a hole. This means that a disc has connectivity one, an annulus (a disc with a hole in the middle) has connectivity two, and the island on the left has connectivity five.
Does the connectivity of the island impact on dividing walls?
What about if you have more tribes on your island? Try introducing more towns of different colours — you will need more walls!
What if our island was the shape of a sphere, rather than a topological disc? Even less likely, consider the same problem on a torus or a Möbius strip.
About the author

Ian Short is a lecturer in mathematics at the Open University. His mathematical interests include complex analysis, continued fractions, dynamical systems, hyperbolic geometry, and uncertainty.
Comments
Great introduction of
Great introduction of topology =)
great (goel)
great work
this stuff
this is confusing:)