September 2008
Finding the Decision Numbers
As discussed in the main article, if the frogs are randomly numbered between 0 and 1, with the prince having the highest number, there is a sequence of decision numbers associated with the best strategy for choosing the top frog. Since we're meant to be doing some maths, we need some notation. We'll consider the general case with 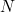 frogs, and let the number on the
frogs, and let the number on the 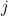 th frog be
th frog be 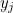 ,
, 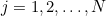 . In addition, we'll try to find an increasing sequence of decision numbers,
. In addition, we'll try to find an increasing sequence of decision numbers, 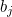 ,
, 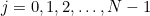 , such that we kiss the
, such that we kiss the 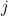 th frog if it has the largest number seen so far and
th frog if it has the largest number seen so far and 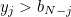 . In other words, to think about kissing the last frog we need
. In other words, to think about kissing the last frog we need 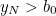 , the next to last frog,
, the next to last frog, 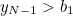 , and so on. The reasons for this back to front numbering of the decision numbers should become clear below.
, and so on. The reasons for this back to front numbering of the decision numbers should become clear below.
Let's assume that the 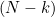 th frog has the largest number so far on its back,
th frog has the largest number so far on its back, 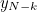 , which we'll write as just
, which we'll write as just 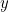 to make things look nicer on the page. There are therefore
to make things look nicer on the page. There are therefore 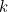 frogs still to come out of the pond. If we kiss the frog, the probability that he's the handsome prince is equal to the probability that the remaining
frogs still to come out of the pond. If we kiss the frog, the probability that he's the handsome prince is equal to the probability that the remaining 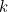 frogs have numbers less than
frogs have numbers less than 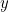 , which is
, which is 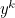 . That's the easy part of the calculation. The next bit is rather more tricky, but basically just involves counting (or combinatorics as it's rather grandly called by mathematicians).
. That's the easy part of the calculation. The next bit is rather more tricky, but basically just involves counting (or combinatorics as it's rather grandly called by mathematicians).
If we don't kiss the frog, but choose the next one with number larger than 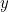 , we can work out the probability that we kiss the prince by considering the situation when there are exactly
, we can work out the probability that we kiss the prince by considering the situation when there are exactly 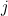 frogs remaining that have numbers higher than the current frog's,
frogs remaining that have numbers higher than the current frog's, 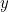 , and adding up our answers for all possible values of
, and adding up our answers for all possible values of 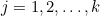 . The probability that there are exactly
. The probability that there are exactly 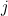 frogs remaining that are numbered higher than
frogs remaining that are numbered higher than 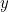 is equal to
is equal to 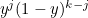 times the number of different ways that we can choose
times the number of different ways that we can choose 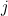 frogs from the final
frogs from the final 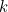 , which is
, which is
The probability that the prince comes
first in the sequence of
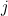
higher-numbered frogs, which is the only position in which he can get kissed, is therefore
The appropriate decision number for the current frog is the value of
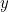
at which the probability of winning by kissing and the probability of winning by not kissing are equal. This gives us, remembering that we must sum over all possible values of
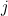
,
or, by defining
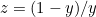
,
Bringing everything over to the right hand side and factoring out the
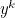
gives
Since
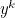
cannot possibly be zero, this leads to the equation
| |
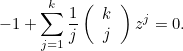 |
|
(1) |
Once we've found the unique positive solution of this,
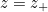
(can you prove there's one and only one positive solution?), the
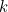
th decision number is given by
| |
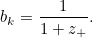 |
|
(2) |
Let's try this for various values of
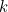
. Note that if you're up to the last frog, you'd obviously kiss it if it's the highest so far, so
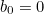
. If
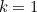
there's just one frog remaining after the current frog. The average value of this final frog is 0.5, so we should kiss the last but one frog if it's the highest we've seen so far and its number satisfies
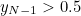
. We therefore expect that the corresponding decision number is
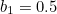
. Now, with
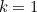
, equation (1) becomes
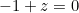
, with the pretty obvious positive solution
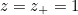
, and hence from equation (2),
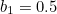
, as expected. When
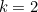
, there are two frogs remaining, and the value of the decision number is less obvious. Equation (1) becomes, after rearranging, the quadratic equation
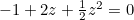
, which has a positive solution
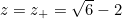
, and hence
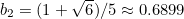
. You should be able to see these last three decision numbers,
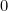
,
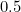
,
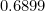
, on the graphs plotted in the main article. We need to solve a cubic equation to find
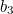
, a quartic equation to find
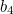
, and so on. Pencil and paper isn't much help here but, because equation (1) has a unique positive solution
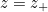
, it's straightforward to find
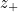
iteratively using Newton's method. You can see the first 100 decision numbers in the graphs in the main article. One other thing we'd like to know is how the decision numbers behave as
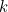
gets large. The maths gets a little harder here, so if you've had
enough, you can
return to the main article.
What happens as k gets large?
We can see from the graphs in the main article that 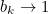 as
as 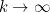 , but how fast does this happen? In order to do this, we need to find the positive solution of equation (1) when
, but how fast does this happen? In order to do this, we need to find the positive solution of equation (1) when 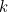 is large. You could have a think about how you might do this before reading on, but I'll warn you that it's not easy. The summed part of equation (1) looks like a binomial series, except for the factor of
is large. You could have a think about how you might do this before reading on, but I'll warn you that it's not easy. The summed part of equation (1) looks like a binomial series, except for the factor of 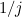 multiplying the terms. However, if we differentiate the series, this goes away. This suggests that we can write the equation as an integral of a binomial series, and a little experimentation shows that equation (1) is equivalent to
multiplying the terms. However, if we differentiate the series, this goes away. This suggests that we can write the equation as an integral of a binomial series, and a little experimentation shows that equation (1) is equivalent to
| |
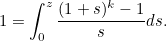 |
|
(3) |
If you don't believe me, use the binomial theorem on
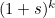
and then integrate the series you get term by term. How does equation (3) help us? Well, integrals are always easier to estimate than sums, and we need to estimate the integral in equation (3) when
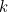
is large. In general,
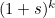
will be large when
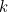
is large, but the left hand side of the equation is just 1. Let's look for a solution with

, and therefore

, small. If we define new variables
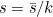
and
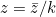
, equation (3) becomes
| |
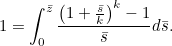 |
|
(4) |
Now
when
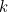
is large. We have used the first term in the Taylor series expansion of
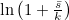
to approximate it here. We can therefore write (4) as
| |
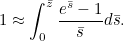 |
|
(5) |
This is now just one equation that we must solve, since we've managed to remove
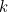
. We can solve this on a computer, approximating the integral using, for example, the trapezium rule, and find the solution
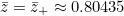
. We now just have to work our way back through our changes of variable; first,
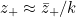
, and then
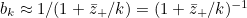
, and hence, applying the binomial theorem to this final result,
We have therefore shown that the decision numbers do, as expected, approach 1 from below as
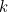
gets large, decaying algebraically, like
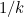
as
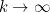
.
Return to main article
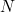 frogs, and let the number on the
frogs, and let the number on the 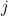 th frog be
th frog be 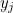 ,
, 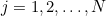 . In addition, we'll try to find an increasing sequence of decision numbers,
. In addition, we'll try to find an increasing sequence of decision numbers, 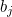 ,
, 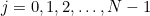 , such that we kiss the
, such that we kiss the 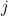 th frog if it has the largest number seen so far and
th frog if it has the largest number seen so far and 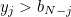 . In other words, to think about kissing the last frog we need
. In other words, to think about kissing the last frog we need 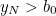 , the next to last frog,
, the next to last frog, 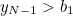 , and so on. The reasons for this back to front numbering of the decision numbers should become clear below.
, and so on. The reasons for this back to front numbering of the decision numbers should become clear below.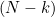 th frog has the largest number so far on its back,
th frog has the largest number so far on its back, 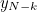 , which we'll write as just
, which we'll write as just 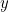 to make things look nicer on the page. There are therefore
to make things look nicer on the page. There are therefore 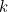 frogs still to come out of the pond. If we kiss the frog, the probability that he's the handsome prince is equal to the probability that the remaining
frogs still to come out of the pond. If we kiss the frog, the probability that he's the handsome prince is equal to the probability that the remaining 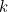 frogs have numbers less than
frogs have numbers less than 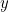 , which is
, which is 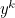 . That's the easy part of the calculation. The next bit is rather more tricky, but basically just involves counting (or combinatorics as it's rather grandly called by mathematicians).
. That's the easy part of the calculation. The next bit is rather more tricky, but basically just involves counting (or combinatorics as it's rather grandly called by mathematicians).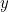 , we can work out the probability that we kiss the prince by considering the situation when there are exactly
, we can work out the probability that we kiss the prince by considering the situation when there are exactly 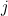 frogs remaining that have numbers higher than the current frog's,
frogs remaining that have numbers higher than the current frog's, 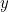 , and adding up our answers for all possible values of
, and adding up our answers for all possible values of 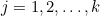 . The probability that there are exactly
. The probability that there are exactly 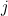 frogs remaining that are numbered higher than
frogs remaining that are numbered higher than 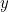 is equal to
is equal to 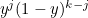 times the number of different ways that we can choose
times the number of different ways that we can choose 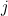 frogs from the final
frogs from the final 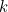 , which is
, which is ![\[ \left( \begin{array}{c} k\\ j \end{array}\right) = \frac{k!}{j! (k-j)!}. \]](/MI/996c9c9a75318421e02b0af942fe0e4e/images/img-0006.png)
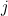 higher-numbered frogs, which is the only position in which he can get kissed, is therefore
higher-numbered frogs, which is the only position in which he can get kissed, is therefore ![\[ \frac{1}{j} \left( \begin{array}{c} k\\ j \end{array}\right) y^{k-j} \left(1-y\right)^ j. \]](/MI/996c9c9a75318421e02b0af942fe0e4e/images/img-0007.png)
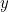 at which the probability of winning by kissing and the probability of winning by not kissing are equal. This gives us, remembering that we must sum over all possible values of
at which the probability of winning by kissing and the probability of winning by not kissing are equal. This gives us, remembering that we must sum over all possible values of 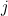 ,
, ![\[ y^ k = \sum _{j=1}^{k} \frac{1}{j} \left( \begin{array}{c} k\\ j \end{array}\right) y^{k-j} \left(1-y\right)^ j, \]](/MI/996c9c9a75318421e02b0af942fe0e4e/images/img-0008.png)
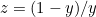 ,
, ![\[ y^ k = \sum _{j=1}^ k \frac{1}{j} \left( \begin{array}{c} k\\ j \end{array}\right) y^ k z^ j. \]](/MI/996c9c9a75318421e02b0af942fe0e4e/images/img-0010.png)
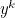 gives
gives ![\[ 0 = y^ k \left(-1 + \sum _{j=1}^ k \frac{1}{j} \left( \begin{array}{c} k\\ j \end{array}\right) z^ j\right) . \]](/MI/996c9c9a75318421e02b0af942fe0e4e/images/img-0012.png)
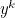 cannot possibly be zero, this leads to the equation
cannot possibly be zero, this leads to the equation 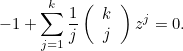
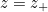 (can you prove there's one and only one positive solution?), the
(can you prove there's one and only one positive solution?), the 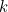 th decision number is given by
th decision number is given by 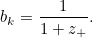
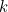 . Note that if you're up to the last frog, you'd obviously kiss it if it's the highest so far, so
. Note that if you're up to the last frog, you'd obviously kiss it if it's the highest so far, so 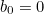 . If
. If 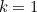 there's just one frog remaining after the current frog. The average value of this final frog is 0.5, so we should kiss the last but one frog if it's the highest we've seen so far and its number satisfies
there's just one frog remaining after the current frog. The average value of this final frog is 0.5, so we should kiss the last but one frog if it's the highest we've seen so far and its number satisfies 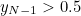 . We therefore expect that the corresponding decision number is
. We therefore expect that the corresponding decision number is 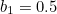 . Now, with
. Now, with 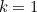 , equation (1) becomes
, equation (1) becomes 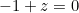 , with the pretty obvious positive solution
, with the pretty obvious positive solution 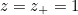 , and hence from equation (2),
, and hence from equation (2), 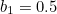 , as expected. When
, as expected. When 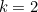 , there are two frogs remaining, and the value of the decision number is less obvious. Equation (1) becomes, after rearranging, the quadratic equation
, there are two frogs remaining, and the value of the decision number is less obvious. Equation (1) becomes, after rearranging, the quadratic equation 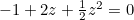 , which has a positive solution
, which has a positive solution 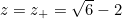 , and hence
, and hence 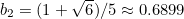 . You should be able to see these last three decision numbers,
. You should be able to see these last three decision numbers, 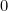 ,
, 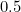 ,
, 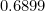 , on the graphs plotted in the main article. We need to solve a cubic equation to find
, on the graphs plotted in the main article. We need to solve a cubic equation to find 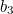 , a quartic equation to find
, a quartic equation to find 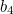 , and so on. Pencil and paper isn't much help here but, because equation (1) has a unique positive solution
, and so on. Pencil and paper isn't much help here but, because equation (1) has a unique positive solution 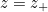 , it's straightforward to find
, it's straightforward to find 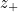 iteratively using Newton's method. You can see the first 100 decision numbers in the graphs in the main article. One other thing we'd like to know is how the decision numbers behave as
iteratively using Newton's method. You can see the first 100 decision numbers in the graphs in the main article. One other thing we'd like to know is how the decision numbers behave as 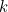 gets large. The maths gets a little harder here, so if you've had
enough, you can return to the main article.
gets large. The maths gets a little harder here, so if you've had
enough, you can return to the main article.
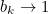 as
as 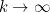 , but how fast does this happen? In order to do this, we need to find the positive solution of equation (1) when
, but how fast does this happen? In order to do this, we need to find the positive solution of equation (1) when 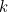 is large. You could have a think about how you might do this before reading on, but I'll warn you that it's not easy. The summed part of equation (1) looks like a binomial series, except for the factor of
is large. You could have a think about how you might do this before reading on, but I'll warn you that it's not easy. The summed part of equation (1) looks like a binomial series, except for the factor of 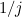 multiplying the terms. However, if we differentiate the series, this goes away. This suggests that we can write the equation as an integral of a binomial series, and a little experimentation shows that equation (1) is equivalent to
multiplying the terms. However, if we differentiate the series, this goes away. This suggests that we can write the equation as an integral of a binomial series, and a little experimentation shows that equation (1) is equivalent to 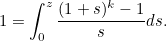
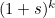 and then integrate the series you get term by term. How does equation (3) help us? Well, integrals are always easier to estimate than sums, and we need to estimate the integral in equation (3) when
and then integrate the series you get term by term. How does equation (3) help us? Well, integrals are always easier to estimate than sums, and we need to estimate the integral in equation (3) when 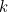 is large. In general,
is large. In general, 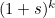 will be large when
will be large when 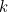 is large, but the left hand side of the equation is just 1. Let's look for a solution with
is large, but the left hand side of the equation is just 1. Let's look for a solution with  , and therefore
, and therefore  , small. If we define new variables
, small. If we define new variables 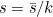 and
and 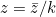 , equation (3) becomes
, equation (3) becomes 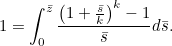
![\[ \left(1+\frac{\bar{s}}{k}\right)^ k = \exp \left\{ k\ln \left(1+\frac{\bar{s}}{k}\right)\right\} \approx \exp \left(\bar{s}\right), \]](/MI/fec0121af8c18bdda78726cceeca870f/images/img-0012.png)
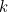 is large. We have used the first term in the Taylor series expansion of
is large. We have used the first term in the Taylor series expansion of 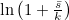 to approximate it here. We can therefore write (4) as
to approximate it here. We can therefore write (4) as 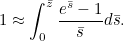
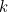 . We can solve this on a computer, approximating the integral using, for example, the trapezium rule, and find the solution
. We can solve this on a computer, approximating the integral using, for example, the trapezium rule, and find the solution 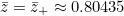 . We now just have to work our way back through our changes of variable; first,
. We now just have to work our way back through our changes of variable; first, 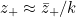 , and then
, and then 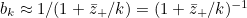 , and hence, applying the binomial theorem to this final result,
, and hence, applying the binomial theorem to this final result, ![\[ b_ k \approx 1 - \frac{\bar{z}_+}{k} \approx 1 - \frac{0.80435}{k}~ ~ ~ \mbox{for $k$ large.} \]](/MI/fec0121af8c18bdda78726cceeca870f/images/img-0018.png)
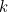 gets large, decaying algebraically, like
gets large, decaying algebraically, like 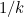 as
as 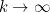 .
.