
Find the number  that satisfies these two properties:
that satisfies these two properties:
- The digits of
 add up to a number
add up to a number 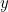 where
where  equals
equals 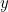 times the number you get when you reverse the digits of
times the number you get when you reverse the digits of 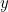 .
. - Reverse the digits of
 and find the prime factors of the number you get. Then take the sum of the squares of these prime factors and halve it. Removing the digit 0 from the new number yields back
and find the prime factors of the number you get. Then take the sum of the squares of these prime factors and halve it. Removing the digit 0 from the new number yields back  .
.
Here's a hint.
This puzzle was contributed by Aziz Inan, Professor of Electrical Engineering at the University of Portland. He chose it in honour of a famous mathematician who would have turned 125 this year.
If you have a puzzle you think might interest Plus readers, please email us!
Solution link
mysterie number
There are two four digit numbers that satisfy condition 1.
1458: sum digits is 18 and 18 ∙ 81 = 1458
1729: sum digits is 19 and 19 ∙ 91 = 1729.
But 1458 does not satisfy condition 2, so we delete it.
1729 does satisfy condition 2: 9271 = 73 ∙ 127 and
(73^2 + 127^2) / 2 = 10729.
Mysterie Number
Agreed. However, I wonder whether this solution is unique. It certainly is the only four digit solution but might there be solutions for numbers larger than 9999?
Kevin
Mystery Number
It is unique. For example, consider a 5-digit number x. The sum of the digits of x represented by y will be maximum 45 (if the number x happens to be 99999). Any 2-digit number y times its reverse (which also consists of maximum 2 digits) will not yield a 5-digit number. In fact, y will consist of maximum 2 digits as long as x has maximum 11 digits. Does this make sense?
Aziz
mystery number
Without taking the hint into account, there are two more numbers satifying condition 1:
1 : sum of digits is 1 and 1 * 1 = 1
81 : sum of digits is 9 and 9 * 9 = 81
Neigther of them satifies the second condition.
mystery number
Submitted by Anonymous on December 18, 2012.
Without taking the hint into account, there are two more numbers satifying condition 1:
1 : sum of digits is 1 and 1 * 1 = 1
81 : sum of digits is 9 and 9 * 9 = 81
Neigther of them satifies the second condition.
the mystery number
between 1000 to 9999 only a single number(1729) satisfies both two properties. here is a 'C' Program to find the number.
#include
#include
main()
{
long x,y,rem,sum,sum1,t,rev,div,flag;
for (x=100;x<=99999;x++)
{
t=x;sum=0;
while(t>0)
{
rem=t%10;
sum=sum+rem;
t=t/10;
}
y=sum;rev=0;
while(sum>0)
{
rev=rev*10+(sum%10);
sum=sum/10;
}
if(x==y*rev)
{
rev=0;sum=x;
while(sum>0)
{
rev=rev*10+(sum%10);
sum=sum/10;
}
div=2;sum1=1;flag=0;
while(rev>1)
{
if(rev%div==0)
{
rev=rev/div;
if(flag==0){
sum1=sum1+(div*div);flag++;}
}
else
{
div=div+1;
flag=0;
}
}
sum1=sum1/2;
printf("x=%d lastno=%d\n",x,sum1);
}
}
getch();
Taxi number
Nice puzzle, and a nice homage to Ramanujan and the taxi number that brought GH Hardy to see him in hospital. Fujiwara (1729) showed 1729 is one of four positive integers (with the others being 81, 1458, and the trivial case 1) which, when its digits are added together, produces a sum which, when multiplied by its reversal, yields the original number.
x in the first part
x = 1729
1+7+2+9 = 19
y=19
19x91= 1729
mistery number
Number 1729 = 1000 ➕ 729 = 10^3 ➕ 9^3 = 12^3 ➕ 1^3 .
maths
Royston designed a game 'The Mystery Number' to help his friends in his study group learn Maths. In this game, 6 times of a mystery number is 2601 more than
1
3
of the same mystery number. Find the mystery number.