March 2010
You might also like to read the first part of this article. This article is about the integral of 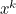 , given by calculus using the formula
, given by calculus using the formula
| |
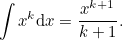 |
|
(1) |
Of course, this equation is only correct for
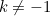
. If we try to take
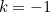
the right hand side is meaningless because we have a zero on the denominator of the fraction, that is
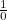
. But in this case we actually know the answer is given by
| |
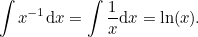 |
|
(2) |
In the first part of this article we derived (1) from first principles, but in this part we are going to examine the somewhat surprising suggestion that really, at a symbolic level, the answer to
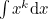
might better be written as
| |
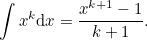 |
|
(1) |
This suggestion was made rather cryptically in the article [1] referenced below. So why is (3) better than (1)?
First consider the (easy) case 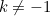 . If we fix
. If we fix 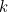 and differentiate
and differentiate 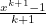 then we obtain
then we obtain
So
is an anti-derivative of
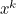
. When
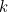
is fixed, the term
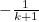
is a number, and so disappears when we differentiate with respect to

. In fact, when we integrate we should really add a constant of integration, so it is arguably better to write (1) as
In formula (3) we have simply chosen a slightly different constant of integration than in (1), but that shouldn't cause any difficulties. What then is the point of (3)? Turning now to the case
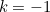
, whereas in (1) we had
in (3) we obtain
Is this any more meaningful, and if so in what way? These are the questions we hope to answer.
Does it matter?

Leonhard Euler, 1707-1783, made significant contributions to the development of calculus.
First let us consider why the exceptional case 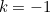 matters. After all, it is only one point out of an infinity of other values for
matters. After all, it is only one point out of an infinity of other values for 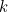 . The formula (1) is valid for all
. The formula (1) is valid for all 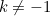 , so why not just ignore this singular awkward case? Intriguingly, in mathematics such exceptional cases occur rather more often than you might expect if you just stuck a pin in the number line, or even if you chose an integer
, so why not just ignore this singular awkward case? Intriguingly, in mathematics such exceptional cases occur rather more often than you might expect if you just stuck a pin in the number line, or even if you chose an integer 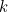 at random. The article [1], where the suggestion that (3) might be better than (1) appears, is concerned with computer algebra systems, which are rather like advanced calculators. They can manipulate algebraic expressions and perform symbolic manipulations such as differentiation and integration. They work at a symbolic level — just as we
are when we are manipulating expressions containing letters to represent numbers — rather than by using approximate numerical values. In a symbolic machine that does not know a value for
at random. The article [1], where the suggestion that (3) might be better than (1) appears, is concerned with computer algebra systems, which are rather like advanced calculators. They can manipulate algebraic expressions and perform symbolic manipulations such as differentiation and integration. They work at a symbolic level — just as we
are when we are manipulating expressions containing letters to represent numbers — rather than by using approximate numerical values. In a symbolic machine that does not know a value for 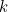 , automatically using the formula (1) might result in an error creeping into a much longer calculation. Mistakes like this are very hard to track down and can lead to serious malfunctioning of the whole program.
, automatically using the formula (1) might result in an error creeping into a much longer calculation. Mistakes like this are very hard to track down and can lead to serious malfunctioning of the whole program.
The special case k=-1 and Euler's special formula
If we try to substitute 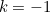 into the right hand side of
into the right hand side of
we end up with the indeterminant form
which is essentially meaningless. To understand what is going on, we need to look at this expression for
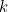
close to
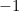
and take a
limit, that is
If we can make sense of this limit, then we will define the value of the expression at
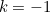
by the value of the limit, thus removing the exceptional case in a meaningful way. This sort of thing is a standard mathematician's move.
To do this we shall make use of a formula discovered by Leonhard Euler. Euler showed that
You can see that this is true in the applet below: use the slider to increase the value of
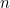
and see the graphs of
get closer and closer to the graph of
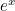
, given by the dotted red line.
|
Use the slider to increase n and see the curves converge. Created with GeoGebra
|
If you are still skeptical, here is a proof of this identity.
At first glance, the limit
appearing in this formula looks very different from the limit we're after, namely
But it turns out that we can transform one into the other. Let's start by considering
Rearranging this we have
and then
Let
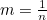
so
Now, set
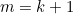
, to give
and we are coming somewhat closer to the right hand side of (3). If
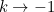
, then

and
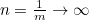
. But if
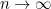
then we may apply Euler's formula to the expression
and conclude that
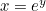
. Taking the inverse gives
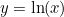
. Hence
The applet below shows how as
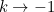
, the graphs of
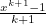
converge to the graph of
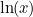
, given by the red dotted line.
|
Use the slider to change the value of k and see the curves converge. Created with GeoGebra
|
So we can say that (3) is indeed valid for all 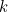 , including the special case
, including the special case 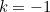 , when we define the value of (3) in this case by the limit
, when we define the value of (3) in this case by the limit 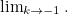 This limit happens to give the right answer to the integral for
This limit happens to give the right answer to the integral for 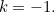 In this sense (3) is indeed somewhat better than (1). The key to all of this is to choose the constant of integration in (1) so that the resulting formula also holds in the awkward limiting case,
In this sense (3) is indeed somewhat better than (1). The key to all of this is to choose the constant of integration in (1) so that the resulting formula also holds in the awkward limiting case, 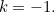 This sort of arbitrary choice looks like a "wizard's trick" the first time you see it, but like many tricks in mathematics it is a technique which occasionally has useful applications elsewhere.
This sort of arbitrary choice looks like a "wizard's trick" the first time you see it, but like many tricks in mathematics it is a technique which occasionally has useful applications elsewhere.
Have a go yourself
If this article has inspired you to do some calculus, here is a problem for you:
Write 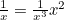 . Integrate the right hand side by parts. Explain why this, and any similar method, fails to find the integral of
. Integrate the right hand side by parts. Explain why this, and any similar method, fails to find the integral of 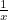 .
.
Reference
[1] D.R. Stoutemyer, Crimes and misdemeanors in the computer algebra trade, Notices of the American Mathematical Society, 38(7):778--785, September 1991.
Chris Sangwin is a member of staff in the School of Mathematics at the University of Birmingham. He has written the popular mathematics books Mathematics Galore!, with Chris Budd, and How
round is your circle? with John Bryant, and edited Euler's Elements of Algebra.
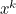 , given by calculus using the formula
, given by calculus using the formula 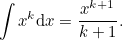
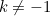 . If we try to take
. If we try to take 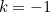 the right hand side is meaningless because we have a zero on the denominator of the fraction, that is
the right hand side is meaningless because we have a zero on the denominator of the fraction, that is 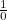 . But in this case we actually know the answer is given by
. But in this case we actually know the answer is given by 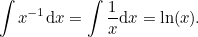
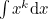 might better be written as
might better be written as 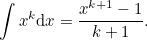
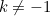 . If we fix
. If we fix 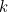 and differentiate
and differentiate 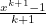 then we obtain
then we obtain ![\[ \frac{\mathrm{d}}{\mathrm{d}x}\frac{x^{k+1}-1}{k+1} = x^ k. \]](/MI/fb06b04a3121561705f10805a154e077/images/img-0004.png)
![\[ \frac{x^{k+1}-1}{k+1}=\frac{x^{k+1}}{k+1}-\frac{1}{k+1} \]](/MI/fb06b04a3121561705f10805a154e077/images/img-0005.png)
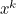 . When
. When 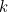 is fixed, the term
is fixed, the term 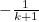 is a number, and so disappears when we differentiate with respect to
is a number, and so disappears when we differentiate with respect to  . In fact, when we integrate we should really add a constant of integration, so it is arguably better to write (1) as
. In fact, when we integrate we should really add a constant of integration, so it is arguably better to write (1) as ![\[ \int x^ k\mathrm{d}x = \frac{x^{k+1}}{k+1}+c. \]](/MI/fb06b04a3121561705f10805a154e077/images/img-0009.png)
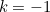 , whereas in (1) we had
, whereas in (1) we had ![\[ \frac{x^{0}}{0}=\frac{1}{0}, \]](/MI/fb06b04a3121561705f10805a154e077/images/img-0011.png)
![\[ \frac{x^{0}-1}{0}=\frac{0}{0}. \]](/MI/fb06b04a3121561705f10805a154e077/images/img-0012.png)

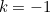 matters. After all, it is only one point out of an infinity of other values for
matters. After all, it is only one point out of an infinity of other values for 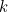 . The formula (1) is valid for all
. The formula (1) is valid for all 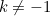 , so why not just ignore this singular awkward case? Intriguingly, in mathematics such exceptional cases occur rather more often than you might expect if you just stuck a pin in the number line, or even if you chose an integer
, so why not just ignore this singular awkward case? Intriguingly, in mathematics such exceptional cases occur rather more often than you might expect if you just stuck a pin in the number line, or even if you chose an integer 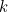 at random. The article [1], where the suggestion that (3) might be better than (1) appears, is concerned with computer algebra systems, which are rather like advanced calculators. They can manipulate algebraic expressions and perform symbolic manipulations such as differentiation and integration. They work at a symbolic level — just as we
are when we are manipulating expressions containing letters to represent numbers — rather than by using approximate numerical values. In a symbolic machine that does not know a value for
at random. The article [1], where the suggestion that (3) might be better than (1) appears, is concerned with computer algebra systems, which are rather like advanced calculators. They can manipulate algebraic expressions and perform symbolic manipulations such as differentiation and integration. They work at a symbolic level — just as we
are when we are manipulating expressions containing letters to represent numbers — rather than by using approximate numerical values. In a symbolic machine that does not know a value for 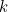 , automatically using the formula (1) might result in an error creeping into a much longer calculation. Mistakes like this are very hard to track down and can lead to serious malfunctioning of the whole program.
, automatically using the formula (1) might result in an error creeping into a much longer calculation. Mistakes like this are very hard to track down and can lead to serious malfunctioning of the whole program.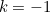 into the right hand side of
into the right hand side of ![\[ \int x^ k\mathrm{d}x = \frac{x^{k+1}-1}{k+1}, \]](/MI/b63c2be88aeed19012b2de6c49bdd061/images/img-0002.png)
![\[ \frac{x^0-1}{0}=\frac{0}{0}, \]](/MI/b63c2be88aeed19012b2de6c49bdd061/images/img-0003.png)
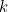 close to
close to 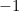 and take a limit, that is
and take a limit, that is ![\[ \lim _{k\rightarrow -1} \frac{x^{k+1}-1}{k+1}. \]](/MI/b63c2be88aeed19012b2de6c49bdd061/images/img-0006.png)
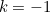 by the value of the limit, thus removing the exceptional case in a meaningful way. This sort of thing is a standard mathematician's move.
by the value of the limit, thus removing the exceptional case in a meaningful way. This sort of thing is a standard mathematician's move.
![\[ e^ x = \lim _{n\rightarrow \infty } \left( 1+\frac{x}{n}\right)^ n. \]](/MI/f3d643bfb5ffe1a48a976d2915501f3d/images/img-0001.png)
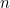 and see the graphs of
and see the graphs of ![\[ \left( 1+\frac{x}{n}\right)^ n \]](/MI/f3d643bfb5ffe1a48a976d2915501f3d/images/img-0003.png)
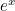 , given by the dotted red line.
, given by the dotted red line.
![\[ \lim _{n\rightarrow \infty }\left( 1+\frac{x}{n}\right)^ n \]](/MI/712deb913d731c0daf93158e2f962fac/images/img-0001.png)
![\[ \lim _{k\rightarrow -1} \frac{x^{k+1}-1}{k+1}. \]](/MI/712deb913d731c0daf93158e2f962fac/images/img-0002.png)
![\[ x = \left( 1+\frac{y}{n}\right)^ n. \]](/MI/712deb913d731c0daf93158e2f962fac/images/img-0003.png)
![\[ x^{\frac{1}{n}} = 1 + \frac{y}{n} \]](/MI/712deb913d731c0daf93158e2f962fac/images/img-0004.png)
![\[ y = n \left(x^{\frac{1}{n}} -1\right). \]](/MI/712deb913d731c0daf93158e2f962fac/images/img-0005.png)
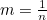 so
so ![\[ y = \frac{1}{m} \left(x^{m}-1\right)=\frac{x^ m-1}{m}. \]](/MI/712deb913d731c0daf93158e2f962fac/images/img-0007.png)
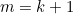 , to give
, to give ![\[ y =\frac{x^{k+1}-1}{k+1} \]](/MI/712deb913d731c0daf93158e2f962fac/images/img-0009.png)
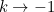 , then
, then  and
and 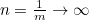 . But if
. But if 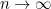 then we may apply Euler's formula to the expression
then we may apply Euler's formula to the expression ![\[ x = \left( 1+\frac{y}{n}\right)^ n. \]](/MI/712deb913d731c0daf93158e2f962fac/images/img-0003.png)
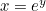 . Taking the inverse gives
. Taking the inverse gives 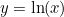 . Hence
. Hence ![\[ \lim _{k\rightarrow -1} \frac{x^{k+1}-1}{k+1} = \ln (x). \]](/MI/712deb913d731c0daf93158e2f962fac/images/img-0016.png)
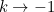 , the graphs of
, the graphs of 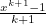 converge to the graph of
converge to the graph of 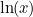 , given by the red dotted line.
, given by the red dotted line.
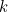 , including the special case
, including the special case 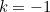 , when we define the value of (3) in this case by the limit
, when we define the value of (3) in this case by the limit 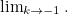 This limit happens to give the right answer to the integral for
This limit happens to give the right answer to the integral for 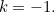 In this sense (3) is indeed somewhat better than (1). The key to all of this is to choose the constant of integration in (1) so that the resulting formula also holds in the awkward limiting case,
In this sense (3) is indeed somewhat better than (1). The key to all of this is to choose the constant of integration in (1) so that the resulting formula also holds in the awkward limiting case, 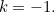 This sort of arbitrary choice looks like a "wizard's trick" the first time you see it, but like many tricks in mathematics it is a technique which occasionally has useful applications elsewhere.
This sort of arbitrary choice looks like a "wizard's trick" the first time you see it, but like many tricks in mathematics it is a technique which occasionally has useful applications elsewhere.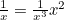 . Integrate the right hand side by parts. Explain why this, and any similar method, fails to find the integral of
. Integrate the right hand side by parts. Explain why this, and any similar method, fails to find the integral of 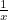 .
.