March 2010
Clock confusion
We all know that homemade presents are supposed to be the best, but the clock your Aunty Mabel made you is a little hard to get used to — the hour and minute hands are exactly the same! You can muddle through most of the time but sometimes, say 26 minutes past 2 or just after 12 minutes past 5, you can't tell which of the two times it is. In the 12-hour period between noon and midnight, how
many moments are there when it is not possible to tell the time on this clock?
Solution
To solve this puzzle we need to figure out exactly which of the possible positions of the hands of the clock are indistinguishable. That is, find all those times such that if you swapped the minute and the hour hands over you also get a valid time.
Let's call the angle the hour hand makes with a line through 12, 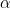 , and the angle the minute hand makes with the line through 12,
, and the angle the minute hand makes with the line through 12, 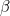 . There is an angle of
. There is an angle of 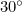 between each number on the clock face. We are actually interested how far past the last number on the clock face each hand has gone, so we can write
between each number on the clock face. We are actually interested how far past the last number on the clock face each hand has gone, so we can write
and
for some integers
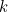
and
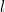
where
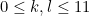
. Then
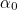
and
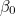
are the amount that each hand has moved past the last number on the clockface, and
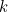
and
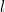
give the last number each hand has passed.
To make sure that swapping the hour and minute hands will give a valid time, we are interested in those times when the proportion of the hour the minute hand has moved through (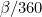 ) is the same as the proportion of the gap between two adjacent numbers the hour hand has moved through (
) is the same as the proportion of the gap between two adjacent numbers the hour hand has moved through (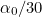 ). Then this time is indistinguishable from the time with the hour and minute hands swapped over. Therefore we can't tell the time whenever
). Then this time is indistinguishable from the time with the hour and minute hands swapped over. Therefore we can't tell the time whenever
| |
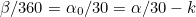 |
|
(1) |
or
| |
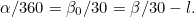 |
|
(2) |
We can rearrange equation (1) to get:
| |
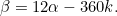 |
|
(3) |
And we can substitute this into equation (2) to get:
And we can substitute this back into (3) to get:
If
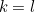
, then the hands lie one top of each other, and swapping the hands gives the same time, so we can still tell the time. However for each of the other
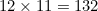
possible pairs of
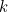
and
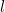
, the time is indistinguishable as by swapping over the hour and minute hands would give a different time. Therefore in the 12 hours from noon we can't tell the time on 132 occasions.
Back to main puzzle page


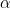 , and the angle the minute hand makes with the line through 12,
, and the angle the minute hand makes with the line through 12, 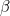 . There is an angle of
. There is an angle of 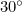 between each number on the clock face. We are actually interested how far past the last number on the clock face each hand has gone, so we can write
between each number on the clock face. We are actually interested how far past the last number on the clock face each hand has gone, so we can write ![\[ \alpha = \alpha _0 + 30k \]](/MI/7f5e983a99a595efc06220222d4cab65/images/img-0004.png)
![\[ \beta = \beta _0 + 30l \]](/MI/7f5e983a99a595efc06220222d4cab65/images/img-0005.png)
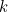 and
and 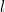 where
where 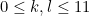 . Then
. Then 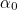 and
and 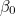 are the amount that each hand has moved past the last number on the clockface, and
are the amount that each hand has moved past the last number on the clockface, and 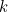 and
and 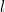 give the last number each hand has passed.
give the last number each hand has passed.
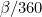 ) is the same as the proportion of the gap between two adjacent numbers the hour hand has moved through (
) is the same as the proportion of the gap between two adjacent numbers the hour hand has moved through (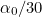 ). Then this time is indistinguishable from the time with the hour and minute hands swapped over. Therefore we can't tell the time whenever
). Then this time is indistinguishable from the time with the hour and minute hands swapped over. Therefore we can't tell the time whenever 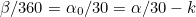
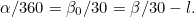
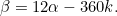
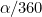
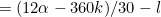
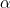
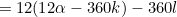
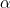
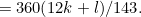
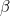
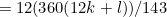

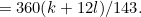
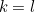 , then the hands lie one top of each other, and swapping the hands gives the same time, so we can still tell the time. However for each of the other
, then the hands lie one top of each other, and swapping the hands gives the same time, so we can still tell the time. However for each of the other 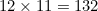 possible pairs of
possible pairs of 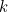 and
and 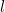 , the time is indistinguishable as by swapping over the hour and minute hands would give a different time. Therefore in the 12 hours from noon we can't tell the time on 132 occasions.
, the time is indistinguishable as by swapping over the hour and minute hands would give a different time. Therefore in the 12 hours from noon we can't tell the time on 132 occasions.
A more intuitive approach
Although correct, I think the above proof doesn't give a good feel for what is going on. After all, this is just a clock -- a good solution ought to be obvious! A more intuitive approach came to me as I was considering the time 12:30. This time is unambiguous because if you treat the minute hand as an hour hand, its associated minute hand (which would point to 12) doesn't coincide with the hour hand. But, if you advance the time by one minute, the hour hand will move 1/12 minute, while the imaginary minute hand will move 12 minutes! It will overtake the hour hand, so at some point must coincide with it. From that key idea, the full proof was easy...
The hour and minute hands coincide at noon. The hour hand revolves once and the minute hand 12 times between noon and midnight; so, allowing for end cases, in that time the hour and minute hands coincide 12 - 1 = 11 times, including noon but excluding midnight.
Consider the minute hand as an hour hand, with an associated "imaginary" minute hand which we will refer to as the "third hand". The third hand revolves 12 times faster than its hour hand (the minute hand) and 12 * 12 = 144 times faster than the hour hand.
If the third hand does not coincide with the hour hand, then the time represented by the hour and minute hands is unambiguous. On the other hand, if the third hand does coincide with the hour hand, the time represented by the hour and minute hands cannot be distinguished from that represented by the minute and third hands -- unless the hour and minute hands coincide, in which case both times are the same and therefore unambiguous.
All three hands coincide at noon. The hour hand revolves once and the third hand 144 times between noon and midnight; so, allowing for end cases, in that time the hour and third hands coincide 144 - 1 = 143 times, including noon but excluding midnight.
As noted above, we must exclude the cases where the hour and minute hands coincide. Hence there are 143 - 11 = 132 ambiguous times on the clock, from noon until just before midnight, occurring in 66 pairs. (If we consider the period from noon to midnight inclusive, noon and midnight constitute an extra pair of ambiguous times.)
a doubt
You mentioned that 12:30 time is unambiguous.. However at 12:30, we would not be able to tell whether it's 12:30 or 6:02:30. Or am I missing something here?
At 6:02:30, the hour hand is
At 6:02:30, the hour hand is *slightly* past the 6. At 12:30 the minute hand is directly on the 6.
The clock is, however, perfectly ambiguous at 12:30:13 and 6:02:31 (approximately).
A more unambiguous example is 6:00.