Blowin' in the wind: solution

Submitted by plusadmin on March 1, 2008
in
March 2008

Blowin' in the wind: solution

In last issue's Outer space we developed a formula for the power output per unit time of a windmill:
  \[ P \approx 0.38 \times (U/10ms^{-1})^3 \; \; kilowatts, \]    
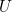where $U$ is the speed of the approaching wind. We deduced that an average wind speed of 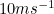$10ms^{-1}$ gives a power output approximately equal to 0.38. The question was why this calculation significantly underestimates the true output.
The answer lies in understanding that the average speed is not a good guide. If, for example, the wind speed was 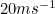$20ms^{-1}$ for half of the time unit and 0 for the other half, then we would get an output approximately equal to
  \[ \frac{1}{2}(0.38 \times 2^3) = 4 \times 0.38. \]    
This is four times more than what we got in the original calculation.
Back to Outer space

Comments

rotation speed of windmill blade

Submitted by Anonymous on September 14, 2012.

If forward wind speeds are 4, 6, 8, 10 m/sec What is the tip speed of a 40m blade at each input rate? (formula?)