December 2008
Black-Scholes in the limit
This section contains some undergraduate level mathematics.
The Binomial model is a very simple model for understanding the ideas behind option pricing. However, so far the stock price can only take finitely many values and furthermore can only move at discrete time points. Both of these features are somewhat undesirable, and so in order to get around this we will look at the limit as the number 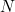 of time periods tends to infinity. This will give us the celebrated Black-Scholes formula.
of time periods tends to infinity. This will give us the celebrated Black-Scholes formula.
Firstly, we will adjust the expression 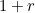 for the value of the bond at time
for the value of the bond at time 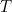 to
to 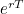 . This isn't an obvious thing to do - it is itself the result of a limiting process. See Plus article Have we caught your interest for more details.
. This isn't an obvious thing to do - it is itself the result of a limiting process. See Plus article Have we caught your interest for more details.
Before taking our limit, it is important that we choose our parameters so that they scale in the correct way. First of all, we fix a terminal time, 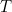 , which is the expiry time of the option. Then set our
, which is the expiry time of the option. Then set our 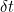 to be given by
to be given by 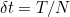 . We will assume that:
. We will assume that:
Furthermore, we assume that the probability of a good or bad period is the same,that is the probability of either period is 1/2 (although as before, this probability won't matter for the option pricing). The stock price at time
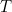
is:
| |
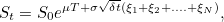 |
|
(1) |
where
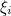
is a random variable which is 1 if the
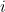
th period was good and -1 otherwise. Now, we need to work out the equivalent probability,
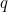
, of an up jump, just as we did before. We have that:
If we use a Taylor expansion on the exponential terms, we see that this gives:
We want to look at the limit as
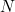
tends to infinity. From our earlier analysis, we should base the price of the option on the behaviour of equation 1, but assuming that the probability of
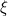
being +1 is given by
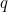
, rather than 1/2. The Central Limit Theorem tells us that if we have a sum of independent and identically distributed variables, which we sum and scale in the correct way, then in the limit we obtain a Normal distribution. To apply the CLT, we must first calculate the expectation of the random terms in the exponential in equation 1. Remember that we must use the probabilities
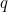
to calculate this expectation:
where we have ignored the
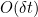
terms. We have can then apply the Central Limit Theorem:
where the convergence is in distribution and
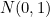
denotes a Normal distribution with mean 0 and variance 1. So we see that in the limit, we should price based on the assumption that:
Note that the true drift of the stock,
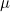
, does not matter for pricing these options, since the value of
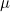
cancels in the expressions above.
We know now that we should base pricing on the formula given above. Therefore, we can now go about pricing the call option mentioned above. The price of this call option is:
where

is the least value of

such that
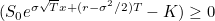
, that is:
We may easily compute this integral (complete the square in the exponential) to obtain the price as:
where
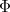
is the cumulative distribution function of a standard Normal random variable and
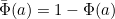
. Rearrangement gives the price as:
where
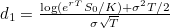
. This is the famous Black-Scholes formula.
Back to main article
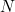 of time periods tends to infinity. This will give us the celebrated Black-Scholes formula.
of time periods tends to infinity. This will give us the celebrated Black-Scholes formula. 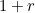 for the value of the bond at time
for the value of the bond at time 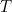 to
to 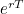 . This isn't an obvious thing to do - it is itself the result of a limiting process. See Plus article Have we caught your interest for more details.
. This isn't an obvious thing to do - it is itself the result of a limiting process. See Plus article Have we caught your interest for more details.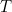 , which is the expiry time of the option. Then set our
, which is the expiry time of the option. Then set our 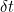 to be given by
to be given by 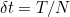 . We will assume that:
. We will assume that: 

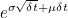
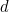

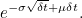
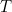 is:
is: 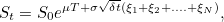
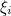 is a random variable which is 1 if the
is a random variable which is 1 if the 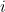 th period was good and -1 otherwise. Now, we need to work out the equivalent probability,
th period was good and -1 otherwise. Now, we need to work out the equivalent probability, 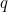 , of an up jump, just as we did before. We have that:
, of an up jump, just as we did before. We have that: ![\[ q = \frac{e^{r \delta t} - u}{u-d} . \]](/MI/6bdbd07ea51f32260a66289b59d91991/images/img-0013.png)
![\[ q = \frac{1}{2} ( 1- \sqrt{\delta t} \frac{ \mu - r + \sigma ^{2}/2}{\sigma }) + O( \delta t). \]](/MI/6bdbd07ea51f32260a66289b59d91991/images/img-0014.png)
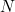 tends to infinity. From our earlier analysis, we should base the price of the option on the behaviour of equation 1, but assuming that the probability of
tends to infinity. From our earlier analysis, we should base the price of the option on the behaviour of equation 1, but assuming that the probability of 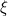 being +1 is given by
being +1 is given by 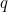 , rather than 1/2. The Central Limit Theorem tells us that if we have a sum of independent and identically distributed variables, which we sum and scale in the correct way, then in the limit we obtain a Normal distribution. To apply the CLT, we must first calculate the expectation of the random terms in the exponential in equation 1. Remember that we must use the probabilities
, rather than 1/2. The Central Limit Theorem tells us that if we have a sum of independent and identically distributed variables, which we sum and scale in the correct way, then in the limit we obtain a Normal distribution. To apply the CLT, we must first calculate the expectation of the random terms in the exponential in equation 1. Remember that we must use the probabilities 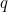 to calculate this expectation:
to calculate this expectation: ![\[ \mathbb {E^{Q}}[ \sigma \sqrt{\delta t} ( \xi _{1} + \xi _{2} + .... + \xi _{N})] & = \sigma \sqrt{\delta t} (2 q - 1) \\ & = -(\mu - r + \sigma ^{2}/2)T, \]](/MI/6bdbd07ea51f32260a66289b59d91991/images/img-0017.png)
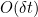 terms. We have can then apply the Central Limit Theorem:
terms. We have can then apply the Central Limit Theorem: ![\[ \sigma \sqrt{ \delta t} ( \xi _{1} + \xi _{2} + .... + \xi _{N}) = \sigma \sqrt{T} \frac{( \xi _{1} + \xi _{2} + .... + \xi _{N})}{\sqrt{N}} \\ \rightarrow _{N \rightarrow \infty } -(\mu - r + \sigma ^{2}/2)T + \sigma \sqrt{T} N(0,1), \]](/MI/6bdbd07ea51f32260a66289b59d91991/images/img-0019.png)
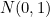 denotes a Normal distribution with mean 0 and variance 1. So we see that in the limit, we should price based on the assumption that:
denotes a Normal distribution with mean 0 and variance 1. So we see that in the limit, we should price based on the assumption that: ![\[ S_{t} = S_{0} e^{ \mu T -(\mu - r + \sigma ^{2}/2)T + \sigma \sqrt{T} N(0,1) } = S_{0} e^{ \sigma \sqrt{T} N(0,1) + (r-\sigma ^{2}/2)T }. \]](/MI/6bdbd07ea51f32260a66289b59d91991/images/img-0021.png)
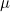 , does not matter for pricing these options, since the value of
, does not matter for pricing these options, since the value of 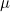 cancels in the expressions above.
cancels in the expressions above. ![$\displaystyle \mathbb {E} [ (S_{T} - K)_{+} ] $](/MI/6bdbd07ea51f32260a66289b59d91991/images/img-0023.png)

![$\displaystyle \mathbb {E} [ (S_{0} e^{ \sigma \sqrt{T} N(0,1) + (r-\sigma ^{2}/2)T } - K)_{+}] $](/MI/6bdbd07ea51f32260a66289b59d91991/images/img-0025.png)


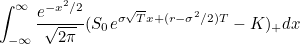


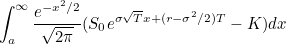
 is the least value of
is the least value of  such that
such that 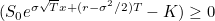 , that is:
, that is: ![\[ a = \frac{\log (K e^{-rT} /S_{0}) + \sigma ^{2}/2}{\sigma \sqrt{T}}. \]](/MI/6bdbd07ea51f32260a66289b59d91991/images/img-0033.png)
![\[ S_{0} \bar{\Phi }(a - \sigma \sqrt{T}) - e^{-r T} K \bar{\Phi }(a), \]](/MI/6bdbd07ea51f32260a66289b59d91991/images/img-0034.png)
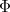 is the cumulative distribution function of a standard Normal random variable and
is the cumulative distribution function of a standard Normal random variable and 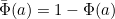 . Rearrangement gives the price as:
. Rearrangement gives the price as: ![\[ \boxed {S_{0} \Phi (d_{1}) - e^{-r T} K \Phi (d_{1}- \sigma \sqrt{T})}, \]](/MI/6bdbd07ea51f32260a66289b59d91991/images/img-0037.png)
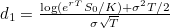 . This is the famous Black-Scholes formula.
. This is the famous Black-Scholes formula.![\[ \]](/MI/6bdbd07ea51f32260a66289b59d91991/images/img-0039.png)