For the question see Puzzle No 8 - The Gobbling Goat in issue 8.
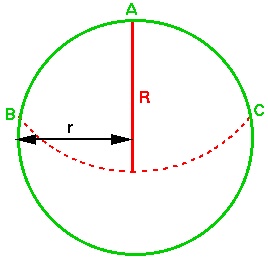
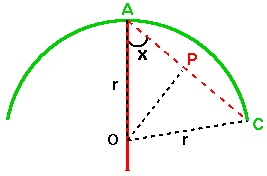
Let the circular field have radius  .
.
Let the length of the rope, which is anchored at point  on the circumference of the field, be
on the circumference of the field, be  .
.
Now, with the rope at full stretch, the goat will be able to move in an arc from point  on the circumference to point
on the circumference to point 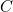 .
.
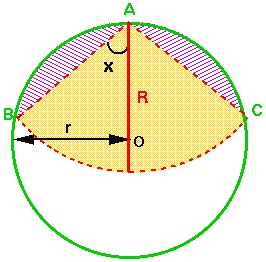
Let  be the centre of the field.
be the centre of the field.
Clearly, the angle  is equal to the angle
is equal to the angle 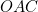 . Let the magnitude of
. Let the magnitude of 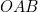 be
be  radians.
radians.
Thus, the area accessible to the goat will be a circle sector with radius 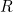 and angle
and angle 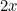 (yellow), plus two circle segments (pink) from a circle of radius
(yellow), plus two circle segments (pink) from a circle of radius  , cut off by the chords
, cut off by the chords 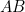 and
and 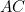 respectively.
respectively.
Now, the area of the circle sector is:
![\[ {1\over 2} (R^2 . 2x) = R^2x \]](/MI/4eb286ba90ab8bc28eaa81fb0a79fa05/images/img-0001.png) |
![\[ (1/2)r^2(\pi -2x) - (1/2)r^2\sin (\pi -2x) \]](/MI/4eb286ba90ab8bc28eaa81fb0a79fa05/images/img-0002.png) |
![\[ R^2x + r^2[\pi - 2x - \sin (2x)] \]](/MI/4eb286ba90ab8bc28eaa81fb0a79fa05/images/img-0003.png) |
Currently, we have two different variables in our area equations:  and
and 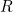 . Let’s try to eliminate one.
. Let’s try to eliminate one.
Obviously, the length of the line segment 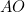 is
is  , the radius of the field. Similarly, the radius of the line segment
, the radius of the field. Similarly, the radius of the line segment 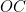 must be
must be  .
.
Therefore, by similar triangles, if we drop a perpendicular from 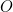 to the line segment
to the line segment 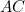 , the perpendicular will bisect
, the perpendicular will bisect 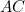 . Therefore the length of
. Therefore the length of 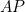 (and
(and 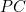 , of course) is
, of course) is 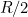 .
.
We now have a right-angled triangle and enough information to calculate the relationship between  and
and 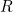 :
:
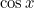 |
 |
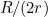 |
(1) | ||
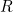 |
 |
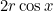 |
(2) |
So the total area accessible to the goat is:
![\[ (4r^2\cos ^2 x)x + r^2[\pi - 2x - \sin (2x)] . \]](/MI/d68c6fae643fb096708b327ea49a13fc/images/img-0015.png) |
We wish for this area to be half the area of the total field; therefore we have:
![$\displaystyle 4r^2 x \cos ^2 x + r^2[\pi -2x-\sin (2x)] $](/MI/d68c6fae643fb096708b327ea49a13fc/images/img-0016.png) |
 |
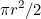 |
|||
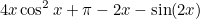 |
 |
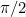 |
|||
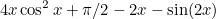 |
 |
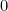 |
We can't easily solve the equation but we can use a graphical calculator or numerical method such as Newton-Raphson to find an approximate solution.
Using the Newton-Raphson method as described in the Coda, we find that
 is approximately
is approximately 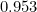 , and therefore
, and therefore 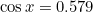 .
.
Now, since 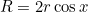 and
and  , the radius of the field, is 100m, we have
, the radius of the field, is 100m, we have 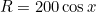 and thus the required length of rope is approximately 116m.
and thus the required length of rope is approximately 116m.
Coda: Solving the equation using Newton-Raphson
The basic idea
In the goat puzzle, we were left with the following equation to solve:
![\[ 4x \cos ^2 x + \pi /2 - 2x - \sin (2x) = 0 \]](/MI/5407992d6a34ad6fe879af4ce063f523/images/img-0001.png) |
The Newton-Raphson method is an approximate method for finding roots of equations that are differentiable.
Let 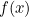 be a differentiable function. Since
be a differentiable function. Since 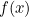 is differentiable, every point on the graph of
is differentiable, every point on the graph of 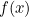 must have a gradient and a unique tangent line.
must have a gradient and a unique tangent line.
Now, the tangent at 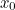 is an approximation to the graph of
is an approximation to the graph of 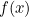 near the point
near the point 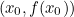 .
.
Therefore the zero of the tangent line (the point where the tangent line crosses the  -axis) is an approximation (perhaps a very bad one, however!) of the zero of
-axis) is an approximation (perhaps a very bad one, however!) of the zero of 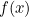 (the point where
(the point where 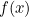 crosses the
crosses the  -axis, i.e. the root of
-axis, i.e. the root of 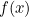 ). It’s like we’re pretending that
). It’s like we’re pretending that 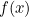 is really a straight line, like the tangent line, and therefore crosses the
is really a straight line, like the tangent line, and therefore crosses the  -axis at the same place the tangent does.
-axis at the same place the tangent does.
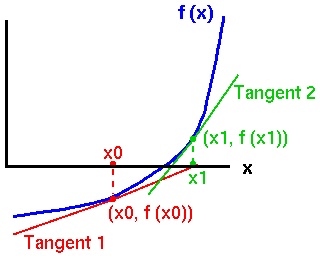
In the Newton-Raphson method, we start with a "best guess" 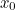 as to the zero of
as to the zero of 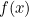 . We then calculate the first approximation,
. We then calculate the first approximation, 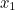 , as the zero of the tangent line to
, as the zero of the tangent line to 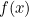 at
at 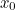 .
.
We then calculate the second approximation, 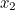 , as the zero of the tangent line crossing the
, as the zero of the tangent line crossing the  -axis at
-axis at 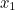 , and so forth.
, and so forth.
The diagram above shows the initial guess 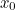 , the first approximations
, the first approximations 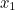 and the relevant tangents. The second approximation
and the relevant tangents. The second approximation 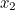 is the coordinate where the second tangent crosses the
is the coordinate where the second tangent crosses the  -axis. As you can see, the approximations are getting closer to the actual zero point of
-axis. As you can see, the approximations are getting closer to the actual zero point of 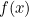 . If we continue iterating like this, we will get better and better estimates for the zero point of
. If we continue iterating like this, we will get better and better estimates for the zero point of 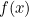 .
.
How do we do it?
We wish to solve 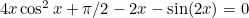 . Obviously, plotting
. Obviously, plotting 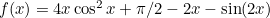 and drawing tangents is not going to be very much fun! However, we can perform Newton-Raphson numerically.
and drawing tangents is not going to be very much fun! However, we can perform Newton-Raphson numerically.
Our initial point is 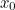 . The gradient of
. The gradient of 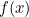 at
at 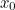 is given by
is given by 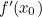 , and the tangent line to
, and the tangent line to 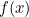 at
at 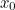 is therefore given by:
is therefore given by:
![\[ y - f(x_0) = f’(x_0) (x - x_0) \]](/MI/8c1d839dc4ac9a0f8071569a88a5c581/images/img-0006.png) |
To find 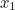 , we must find the point where this tangent crosses the
, we must find the point where this tangent crosses the  -axis, i.e. to let:
-axis, i.e. to let:
![\[ 0 - f(x_0) = f’(x_0) (x_1 - x_0) \]](/MI/8c1d839dc4ac9a0f8071569a88a5c581/images/img-0009.png) |
and therefore
![\[ x_1 - x_0 = \frac{-f(x_0)}{f'(x_0)} \]](/MI/8c1d839dc4ac9a0f8071569a88a5c581/images/img-0010.png) |
so that
![\[ x_1 = x_0 - \frac{f(x_0)}{f'(x_0)} \]](/MI/8c1d839dc4ac9a0f8071569a88a5c581/images/img-0011.png) |
Similarly, in the general case we obtain:
![\[ x_{n+1} = x_ n - \frac{f(x_ n)}{f'(x_ n)} \]](/MI/8c1d839dc4ac9a0f8071569a88a5c581/images/img-0012.png) |
Now, our function is 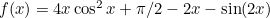 . Via standard differential calculus, the gradient
. Via standard differential calculus, the gradient 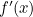 of this function is
of this function is
![\[ 4 \cos ^2 x - 8x \cos x \sin x - 2 - 2 \sin (2x) \cos (2x). \]](/MI/8c1d839dc4ac9a0f8071569a88a5c581/images/img-0015.png) |
Therefore, to find the approximate root of 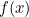 we can use the following:
we can use the following:
![\[ x_{n+1} = {x_ n} - \frac{4x_ n \cos ^2 x_ n + \pi /2 - 2x_ n - \sin (2x_ n)}{4\cos ^2 x_ n - 8x_ n \cos x_ n \sin x_ n - 2 - 2 \sin (2x_ n) \cos (2x_ n)} \]](/MI/8c1d839dc4ac9a0f8071569a88a5c581/images/img-0016.png) |
So, we know how to calculate 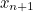 from
from 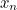 . But how do we find our starting value,
. But how do we find our starting value, 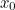 ? Well, in this particular case we know that the magnitude of
? Well, in this particular case we know that the magnitude of  must be between 0 and
must be between 0 and 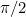 radians (go back to the second diagram and think about it if you’re not sure why!). So a good initial guess might be (for example)
radians (go back to the second diagram and think about it if you’re not sure why!). So a good initial guess might be (for example) 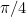 .
.
As it turns out, all sorts of values will do: here’s a table of the iterative steps of Newton-Raphson on our function 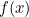 for a range of initial values of
for a range of initial values of 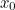 . As you can see, they all converge quite rapidly to the same twelve-significant-digit approximation.
. As you can see, they all converge quite rapidly to the same twelve-significant-digit approximation.
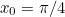 |
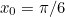 |
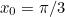 |
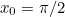 |
|
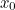 |
0.785398163397 | 0.523598775598 | 1.047197551200 | 1.570796326790 |
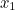 |
0.967088277214 | 1.254847487960 | 0.956164730983 | 0.785398163397 |
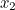 |
0.953058379193 | 0.966611488070 | 0.952884951928 | 0.967088277214 |
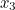 |
0.952849994306 | 0.953049230238 | 0.952848237620 | 0.953058379193 |
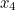 |
0.952847886046 | 0.952849901115 | 0.952847868401 | 0.952849994306 |
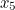 |
0.952847864870 | 0.952847885110 | 0.952847864693 | 0.952847886046 |
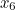 |
0.952847864657 | 0.952847864860 | 0.952847864655 | 0.952847864870 |
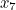 |
0.952847864655 | 0.952847864657 | 0.952847864655 | 0.952847864657 |
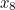 |
0.952847864655 | 0.952847864655 | 0.952847864655 | 0.952847864655 |
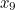 |
0.952847864655 | 0.952847864655 | 0.952847864655 | 0.952847864655 |
You can simplify the equation by using the cos(2x) trig identity
4 x cos^2(x) + pi/2 - 2x - sin(2x) = 0
can be simplified a little using cos(2x) = 2 cos^2(x) - 1
You get:
2 x cos(2x) + pi/2 - sin(2x) = 0
or replacing variables (y = 2x):
y cos(y) + pi/2 - sin(y) = 0