Unveiling the Mandelbrot set

Share this page
September 2006

The filled Julia set of x2 + 0

To work out the filled Julia set of x2 + 0 = x2 we need to look at all the points on the complex plane and decide whether or not their orbits escape to infinity. Those whose orbit doesn't escape are part of the filled Julia set.

Let's start with a complex number a + ib and let's assume that its distance from the complex number 0 is greater than 1. On the plane, the number a + ib is represented by the point with co-ordinates (a,b) and 0 is the point with co-ordinates (0,0).
This means that a + ib has distance 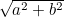$\sqrt{a^2+ b^2}$ from 0, and so, by our assumption, we have

  \[ \sqrt{a^2+ b^2} > 1. \]    

Now using a + ib as the seed x0 we get

  \[ x_1 = (a + ib)^2 = a^2- b^2 + i2ab, \]    
So the distance of x1 to 0 is
  \[ \sqrt{(a^2- b^2)^2 + 4a^2b^2}. \]    
So is x1 closer to 0 than x0 or further away? Well, we have
  \[ (a^2 - b^2)^2 + 4a^2b^2 \, \, = \, \, a^4 - 2a^2 b^2 + b^4 + 4a^2b^2\, \, = \, \, a^4 + 2a^2b^2 + b^4\, \, = \, \, (a^2 + b^2)^2. \]    
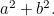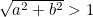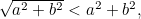Hence, the distance of x1 to 0 is $a^2 + b^2.$ But since $\sqrt{a^2 + b^2} > 1$ we know that $\sqrt{a^2 + b^2} < a^2 + b^2,$ and so x1 is further away from 0 than x0. Repeating this argument shows that x2 is further away from 0 than x1, x3 is further away from 0 than x2, and so forth. In other words, points in the orbit of x0 move further and further out — the orbit tends to infinity. This means that x0 does not lie in the filled Julia set. And since x0 represented any point with distance greater than 1 from 0, we know that no such point can lie in the filled Julia set.

A very similar calculation shows that if the distance between x0 = a + ib and 0 is less than 1, then x1 is closer to 0 than x0, and this means that the orbit cannot possibly tend to infinity. So points whose distance is to 0 is less than 1 lie in the filled Julia set.

And what if the distance between x0 = a + ib and 0 is equal to 1? A calculation shows that the distance between x1 and 0 is also equal to 1. Thus, points in the orbit of x0 always remain at distance 1 from 0 — the orbit does not tend to infinity and therefore x0 lies in the filled Julia set.

We've now accounted for all the points on the plane and seen that only those whose distance to 0 is less than or equal to 1 belong to the filled Julia set. The filled Julia set, then, is the disc in the plane with centre 0 and radius 1.

If you are familiar with complex numbers the calculation is actually easier. In this case you will know that a complex number x0 = x + iy can be written as x0 = reiθ, where r is its distance to the point 0 and θ is the angle that the line from 0 to x0 makes with the x-axis. Now x1 = r2e2iθ, so x1 has distance r2 from 0. This means that x1 is further a way from 0 than x0 precisely when r > 1.

Return to the article