September 1999

Are you going to be a good customer for your bank? This might not worry you, but it certainly worries your bank! Banks would like to be able to predict both who their most profitable clients are likely to be, and which potential clients are most likely to be unreliable or a poor risk.

Sadly for the banks, human beings are unpredictable creatures and it's not always easy to guess correctly how a particular client will behave. Banks are always looking for better ways of doing this, and recently nineteen financial institutions, including all the British High Street banks, got together to back a new research project.

The project is being run by NCR, an electronics company, and involves five mathematicians from Imperial College, London. It wil examine whether a technique known as Bayesian Inference might be better than current methods for predicting customer behaviour.

In the late eighteenth century, Thomas Bayes described his famous theorem about conditional probability:

$P(A | B) = \frac{P(B | A) P(A)}{P(B)}$

(see the Coda for an explanation and a more detailed discussion).

While Bayes' Theorem is trivially true for "point probabilities", where each of the probabilities involved has a single definite value (as described in our example), it can also be used for manipulating probability distributions: that is, Bayes' Theorem applies as much to probability density functions as it does to point probabilities. It can be used to calculate the spread of probability over a whole range of possible outcomes, taking into account a whole range of differently likely factors. This makes it a very rich and flexible tool for the kinds of complex predictions that banks would like to make.

Dr Stephen Emmott from NCR is hopeful about this new commercial application of Bayes' Theorem. "We think it has the potential for revolutionising how banks and retailers interact with their customers by being able to predict more accurately what they want." Current trials involving the Canadian Imperial Bank of Commerce (CIBC) seem to be going well: the Vice-President of Marketing, Rick Miller, says that "We're seeing tangible results by applying Bayes' theorem over our existing statistical models - we can better read our customers' needs".

What's the upshot for mathematicians in all of this? If the Bayesian technique pays off, the banks will pay up: one recruitment specialist predicted six-figure fees being offered to mathematicians with the requisite skills in Bayesian theory.

Coda: Conditional Probability and Bayes' Theorem

Conditional Probability

What is a conditional probability? It is the probability of some event given that some other event has already occurred.

Let's look at an example.

A group of 100 secondary schools have been sent a questionnaire, asking whether or not they have a gym and whether or not they have a swimming pool. It turns out that the results are as follows:

GYM	NO GYM	TOTAL
73	27	100

POOL	NO POOL	TOTAL
24	76	100

So, we now know the following:

The probability that a randomly selected school from this population has a gym is 73/100 or 0.73. In other words:

$P(Gym) = 0.73$
The probability that a randomly selected school from this population has a pool is 24/100 or 0.24. In other words:

$P(Pool) = 0.24$

Note, of course, that the following must be true:

$P(No Gym) = 1-P(Gym) = 0.27$

$P(No Pool) = 1-P(Pool) = 0.76$

However, let's say we're interested in whether schools that have a gym are more likely to have a pool than schools that don't have a gym. At the moment, we can't decide that from the statistics we have. Therefore we go back to the questionnaire and produce a different table of results.

This time, we look at schools with gyms and schools without gyms as separate populations, and count up how many schools in each population have pools and don't have pools:

	POOL	NO POOL	TOTAL
GYM	21	52	73
NO GYM	3	24	27
TOTAL	24	76	100

Now we can reach some more conclusions.

Of the 73 schools with gyms, 21 also have pools. Therefore, if we pick a random school from the schools with gyms, the probability that this school also has a pool is 21/73 or roughly 0.288.

This is known as a conditional probability. It is notated as follows:

$P(Pool | Gym) = 0.288$

which translates as "Given that the school has a gym, the probability that it has a pool is 0.288".
Of the 27 schools without gyms, 3 have pools. Therefore, if we pick a random school from the schools without gyms, the probability that this school has a pool is 3/27 or roughly 0.111. In other words:

$P(Pool | No Gym) = 0.111$

Again, note that the following relationships must obviously hold:

$P(No Pool | Gym) = 1-P(Pool | Gym) = 0.712$

$P(No Pool | No Gym) = 1-P(Pool | No Gym) = 0.889$

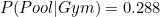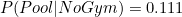We can now answer our question. Since $P(Pool | Gym) = 0.288$ and $P(Pool | No Gym) = 0.111$ , we can observe that schools with gyms are more likely to have pools than schools without gyms.

Question

Given that school X has a pool, what is the probability that it also has a gym?

(Note that you can answer this question directly from the questionnaire results, or you can answer it using Bayes' Theorem, described below).

Bayes' Theorem for point probabilities

In 1763, the Royal Society published an article entitled An Essay towards solving a Problem in the Doctrine of Chances by the Reverend Thomas Bayes (Philosophical Transactions of the Royal Society, Volume 53, pages 370-418, 1763).

The article was found amidst Bayes' papers after his death, and published posthumously. In it Bayes develops his famous theorem about conditional probability:

$P(A | B) = \frac{P(B | A) P(A)}{P(B)}$

In other words, the probability of some event A occurring given that event B has occurred is equal to the probability of event B occurring given that event A has occurred, multiplied by the probability of event A occurring and divided by the probability of event B occurring.

What is Bayes' Theorem useful for? The best way to understand this is with another example.

Let's say we have some population of people who we are testing for the rare disease called Innumeratica. We expect the disease is present in about 0.1 percent of that population (one person in 1000).

Unfortunately, the test we are using is not entirely reliable. If a person has the disease and is tested, then 95 percent of the time the test will show positive (the correct result), but 5 percent of the time the test will show negative: a "false negative".

If a person does not have the disease and is tested, then 90 percent of the time the test will show negative (the correct result), but 10 percent of the time the test will show positive: a "false positive".

Thus we can observe the following about our population:

$P(Disease) = 0.001$

$P(No Disease) = 0.999$

$P(Positive test | Disease) = 0.95$

$P(Negative test | Disease) = 0.05$

$P(Negative test | No disease) = 0.90$

$P(Positive test | No disease) = 0.10$

Let's say we pick a subject from the population and test him, and the test comes back positive. The subject is therefore very worried that he might have the disease. How likely is it that he really has the disease, as opposed to the test being just a false positive? We can work this out using Bayes' Theorem.

We want to know the probability that the subject has the disease, given that his test was positive. From Bayes' Theorem, we have:

$P(Disease | Positive test) = \frac{P(Positive test | Disease) P(Disease)}{P(Positive test)}$

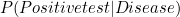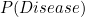Now, we already know $P(Positive test | Disease)$ and $P(Disease)$ . We can also observe that

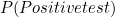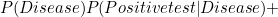	$\displaystyle P(Positive test)$	$\displaystyle =$	$\displaystyle P(Disease) P(Positive test \| Disease) +$		(1)
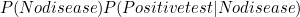	$\displaystyle$	$\displaystyle$	$\displaystyle P(No disease) P(Positive test \| No disease)$		(2)

(i.e. we have to consider both true positives and false positives, and the relative probability of each, in working out the overall probability of a positive result), and thus

$P(Positive test) = (0.001 \times 0.95) + (0.999 \times 0.10) = 0.101$

Thus, we can substitute these known probabilities into Bayes’ Theorem to find out 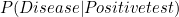$P(Disease | Positive test)$ :

$P(Disease | Positive test) = \frac{0.95 \times 0.001}{0.101} = 0.0094$

In other words, there is a less than one percent chance that the subject actually has the disease, even though he tested positive. There is a greater than 99 percent chance that the test was a false positive. The test subject will be glad to hear it!

Question

A random person is chosen from the population and tested. Her test comes back negative. What is the probability that she actually has the disease (ie the test is a false negative)?

Plus.Maths.org

Ye banks and Bayes

Coda: Conditional Probability and Bayes' Theorem

Conditional Probability

Question

Bayes' Theorem for point probabilities

Question

See also