Maths in a minute: Utility theory
How much is a £100 worth to you? That might seem like an obvious question, but the value might be different for different people: £100 is worth a lot more to someone in poverty compared to a millionaire. And it might be worth a lot less if there is some risk involved. So how do you value how much something is worth, if the value will be relative depending on who you ask?
The answer comes from utility theory, which gotes back to John von Neumann and Oskar Morgenstern's work of the 1940s. Von Neumann and Morgenstern realised that to model something as subjective as perception of risk, you have to measure not the real, objective value of things - money or goods - but the relative value of these things to an individual. This value is called the utility.
Let's look at an example: suppose I flip a coin and you win £1000 if heads comes up, and lose £1000 if tails comes up. You have a 50:50 chance of winning. If you like a bit of a gamble you might accept this, but if you're more cautious, then the risk of losing £1000 may be unacceptable to you. You may feel that the potential gain of £1000 is simply not worth as much as the £1000 you already have. To persuade you to accept my gamble I might have to offer you a potential gain of, say, £10,000. You would then accept the gamble if the risk of losing the £1000 you already have means less to you than the possibility of winning £10,000.
Economists model this subjective value of money or goods by a utility function. A simple example of this is the function 
, where 
is your wealth, and 
and 
are some fixed numbers.
and 
. If 
is less than one, then the slope of the function decreases with your wealth 
- the function becomes flatter as gets larger. As your wealth increases, the utility, or subjective value, of it increases more and more slowly. In our example, £1000 has utility 
. To find an amount that has twice that utility value, we have to go all the way up to £10,080.
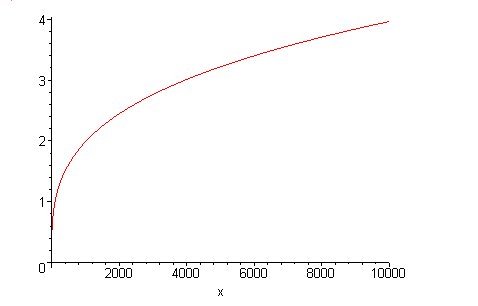
This means that you are "risk-averse": the difference of £9080 between the £1000 and the £10,080, to you is only worth as much as the initial £1000. You're only prepared to take a risk on your £1000 if the potential gain is a lot more. The number 
is a measure for your risk averseness: the smaller it is, the flatter the curve, and the greater the amount I'd have to offer you before you're prepared to accept. More generally, the function measuring the utility of something in a given context doesn't need to take the form it does in our example: it could take any form you think is appropriate in the context.
Utility theory may also use utility tables to compare the relative value of various scenarios to the different people they involve, something that is widely used in game theory and economics. You can find out more about how utility theory can be used in practice in Can maths help improve the communities of the future? and How to measure a million.
This article is part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI), an international research centre and our neighbour here on the University of Cambridge's maths campus. INI attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
