The shower equation: Dealing with delay
We've all been there. You're in the shower and the water feels too cold, so you turn up the hot tap. Nothing happens immediately because it takes the hot water time to get around the pipes, so you end up turning the heat up higher. Eventually the water gets around the pipes, into the shower and onto you. It is then far too hot. You immediately turn the hot water down, but by the time the effect gets to you the water is too cold. So you turn the heat up again. And so the cycle continues — it seems impossible to get it right.
It turns out there's an equation which describes this situation. And this equation has applications well beyond the bathroom, from climate change to COVID-19. That's because lots of processes in the world involve an effect that only sets in after a delay. But before we get there, let's have a look at the equation.
The equation
Let’s write 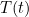 for the temperature of the water as we feel it at time
for the temperature of the water as we feel it at time 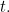 Suppose that it takes a time of
Suppose that it takes a time of 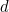 seconds for the water to get around the plumbing. Then the shower equation is
seconds for the water to get around the plumbing. Then the shower equation is
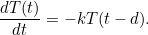 |
(1) |
Let’s walk through this expression. The 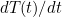 on the left denotes the rate of change of the temperature of the water at time
on the left denotes the rate of change of the temperature of the water at time  . If this has a positive value then the temperature is increasing at time
. If this has a positive value then the temperature is increasing at time  , and if it has a negative value then the temperature is decreasing at time
, and if it has a negative value then the temperature is decreasing at time  . The higher the positive value (or the smaller the negative value), the faster the temperature is increasing (or decreasing) at time
. The higher the positive value (or the smaller the negative value), the faster the temperature is increasing (or decreasing) at time 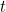 .
.

The right-hand side of the equation tells us that this rate of change at time 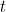 is proportional to the temperature you had
is proportional to the temperature you had 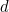 seconds before time
seconds before time 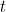 , that is, it is proportional to
, that is, it is proportional to 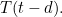 This makes sense: the rate at which the temperature is changing at time
This makes sense: the rate at which the temperature is changing at time 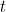 depends on how much you turned the heat up (or down) at time
depends on how much you turned the heat up (or down) at time 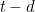 , which obviously depends on how hot or cold you felt the water to be back then. The number
, which obviously depends on how hot or cold you felt the water to be back then. The number 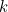 is just the (positive) constant of proportionality here (which we assume to be greater than
is just the (positive) constant of proportionality here (which we assume to be greater than 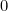 ).
).
Finally, the minus sign reflects the fact that a high temperature at time 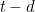 means you turned the heat down, leading to a decreasing temperature at time
means you turned the heat down, leading to a decreasing temperature at time 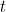 , while a low temperature at time
, while a low temperature at time 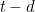 means you turned the heat up, leading to an increasing temperature at time
means you turned the heat up, leading to an increasing temperature at time 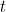 .
.
(OK, there’s a bit of a fudge here: strictly speaking the equation says you’d turn the heat up if the temperature is below 0 and down if it’s above 0. This clearly isn’t quite right, as just above 0 is nowhere near warm enough. However, the equation could be easily adjusted to reflect the fact that you turn the heat up or down depending on whether the temperature is below or above some ideal value other than 0.)
Solving this equation means finding the function 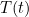 which satisfies it. This function would then give you the temperature
which satisfies it. This function would then give you the temperature 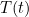 for any time
for any time 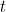 . Knowing the function will tell you whether your turning of taps will ever settle you down at a comfortable temperature or keep going on forever without a satisfying result.
. Knowing the function will tell you whether your turning of taps will ever settle you down at a comfortable temperature or keep going on forever without a satisfying result.
Because our equation involves a rate of change, which is also called a derivative, the equation is called a differential equation. Such equations are rarely easy to solve, but we can at least start exploring what the solutions might look like. This involves a bit of calculus. If you are not up for that you might want to skip to the last part of this article, where we will look at important applications of the shower equation.
Without delay
Let’s first see what would happens if it took the water no time at all to get through the pipe, so there’s no delay and 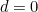 . Our equation (1) would become
. Our equation (1) would become
![\[ \frac{dT(t)}{dt} = -kT(t). \]](/MI/7f563c2e8ae2d0c9c32e6b1373569c57/images/img-0002.png) |
If you know a bit about differentiation you will know that the function
![\[ T(t)=e^{-kt} \]](/MI/7f563c2e8ae2d0c9c32e6b1373569c57/images/img-0003.png) |
is a solution in this case. Below is a plot of this function for different values of 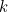 (use the slider to change
(use the slider to change 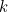 ). In each case we can see that the behaviour of temperature is stable: it converges to a value of 0 (which through the fudge mentioned above we assume to be the ideal temperature we are aiming for).
). In each case we can see that the behaviour of temperature is stable: it converges to a value of 0 (which through the fudge mentioned above we assume to be the ideal temperature we are aiming for).
With delay
When there is a delay, so 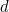 is not equal to 0, the maths gets harder, so feel free to skip to the end of the article where we look at applications of the equation.
is not equal to 0, the maths gets harder, so feel free to skip to the end of the article where we look at applications of the equation.
Let’s assume the solution to have the form
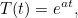 |
(2) |
for some 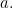 Our task is to figure out what the parameter
Our task is to figure out what the parameter  should be. Differentiating (2) with respect to
should be. Differentiating (2) with respect to 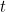 gives
gives
![\[ \frac{dT(t)}{dt}=ae^{at}. \]](/MI/b033285219c0294ac32f40a408144427/images/img-0005.png) |
Putting this into the original equation (1) gives
![\[ ae^{at} = -k e^{a(t-d)}=-ke^{at}e^{-ad}. \]](/MI/b033285219c0294ac32f40a408144427/images/img-0006.png) |
This equation holds precisely when the parameter  satisfies the transcendental equation
satisfies the transcendental equation
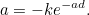 |
(3) |
We can make this look a tiny bit neater by writing
![\[ x=-ad. \]](/MI/5e82fb204faea3b4faba929e6bd959aa/images/img-0002.png) |
Then equation (3) becomes
![\[ -\frac{x}{d}=-ke^ x, \]](/MI/5e82fb204faea3b4faba929e6bd959aa/images/img-0003.png) |
so
![\[ x=kd e^ x. \]](/MI/5e82fb204faea3b4faba929e6bd959aa/images/img-0004.png) |
Transcendental equations are hard to solve, but one thing we can do is plot the two functions 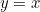 and
and 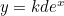 and see where they intersect. The
and see where they intersect. The  -coordinate of these intersection points satisfy equation (3). We have done this below: use the slider to change the value of
-coordinate of these intersection points satisfy equation (3). We have done this below: use the slider to change the value of 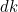 .
.
The plot shows that equation (3) only has solutions when when 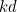 is smaller than some value around 0.37. In fact, it turns out that it has solutions only if
is smaller than some value around 0.37. In fact, it turns out that it has solutions only if
![\[ kd<1/e \approx 0.3679..., \]](/MI/f824f590d2aa6c91ee521e6df9035993/images/img-0002.png) |
where  is the base of the natural logarithm.
is the base of the natural logarithm.
The solutions  in this case will be positive numbers. Since
in this case will be positive numbers. Since 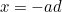 and
and 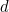 is also positive (remember it represents the delay), this means that
is also positive (remember it represents the delay), this means that 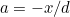 is a negative number. The solution
is a negative number. The solution
![\[ T(x)=e^{ax} \]](/MI/f824f590d2aa6c91ee521e6df9035993/images/img-0008.png) |
of the original shower equation (1) then has a similar shape to the one shown for the case where there is no delay: it will tend towards 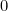 as time goes on. In other words, if the product of our delay parameter
as time goes on. In other words, if the product of our delay parameter 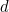 and the constant of proportionality
and the constant of proportionality 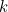 is less than or equal to
is less than or equal to 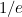 , our turning of taps will eventually bring us to our ideal temperature.
, our turning of taps will eventually bring us to our ideal temperature.
What happens if  ? Then we need to venture into the land of complex numbers: equation (3) in this case has no real solutions, but it does have complex solutions. We won't get into the details here, but it turns out that if the real part of these complex solutions is less than 0, the shower situation remains controllable: the turning of taps will eventually get us to the desired temperature. If the real part of the complex solution is greater than 0, however, then the shower is not controllable: the temperature will keep going up and down and we will never be happy.
? Then we need to venture into the land of complex numbers: equation (3) in this case has no real solutions, but it does have complex solutions. We won't get into the details here, but it turns out that if the real part of these complex solutions is less than 0, the shower situation remains controllable: the turning of taps will eventually get us to the desired temperature. If the real part of the complex solution is greater than 0, however, then the shower is not controllable: the temperature will keep going up and down and we will never be happy.
In terms of our delay parameter 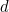 and our proportionality constant
and our proportionality constant 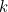 , the transition between these two situations happens when the product
, the transition between these two situations happens when the product 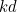 is equal to
is equal to 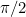 .
.
Climate change and COVID-19
If you have skipped the mathsy section, then welcome back! The conclusion we arrived at in that section is that if the product 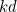 (of our delay parameter
(of our delay parameter 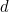 and our proportionality constant
and our proportionality constant 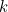 ) is less than
) is less than 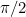 , the shower situation is controllable: turning the taps will eventually settle us at our desired temperature. When
, the shower situation is controllable: turning the taps will eventually settle us at our desired temperature. When 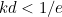 this happens without any oscillation and when
this happens without any oscillation and when 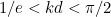 then there’ll be some oscillation around the ideal temperature before things settle down. This is illustrated in the following two graphs.
then there’ll be some oscillation around the ideal temperature before things settle down. This is illustrated in the following two graphs.
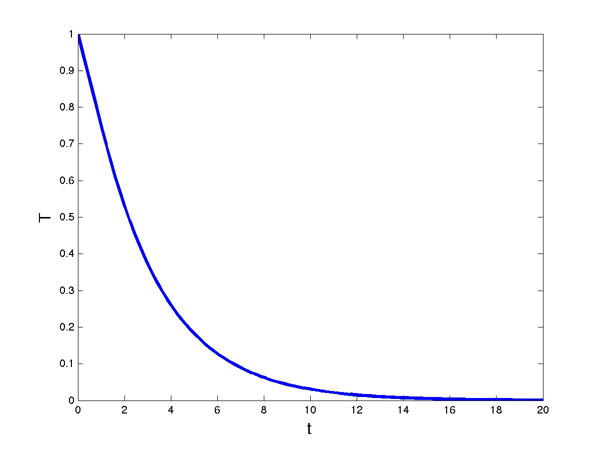
The temperature function for kd=0.25 < 1/e.
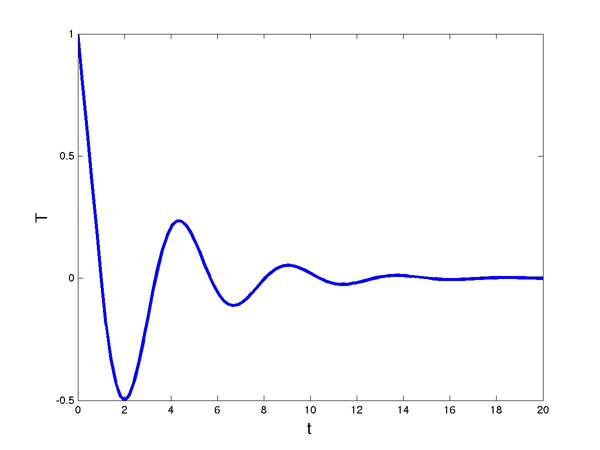
The temperature function for 1/e < kd=1 < π/2.
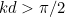 , then the temperature will keep oscillating wildly, as demonstrated by the following plot.
, then the temperature will keep oscillating wildly, as demonstrated by the following plot.
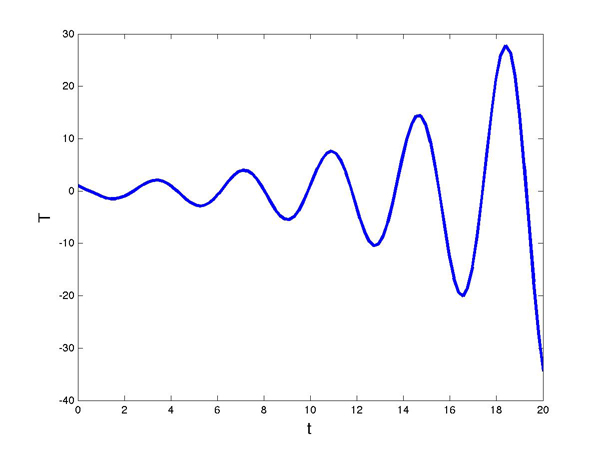
The temperature function for kd=2 > π/2.
Now, as promised, let's look at other applications of our shower equation. One of the most important of these is in the study of the dynamics of the climate. The reason for this is that many climate phenomena take time to have an effect.
For example, if we change the amount of carbon dioxide that we put into the atmosphere now, then we will have to wait some time before we see the actual effects of this on the Earth's temperature. This makes it hard to determine the effects of carbon dioxide reduction, and can potentially lead to uncontrolled oscillations.
Another example involves the El Niño Southern Oscillation (ENSO). This is an irregular change in the temperature in the tropical Pacific ocean with an approximate four year interval between warming events. El Niño has a major effect on the economy, not only in the region where it occurs, but all over world. If we could predict it better, then this would help the communities in the Pacific to prepare for it.
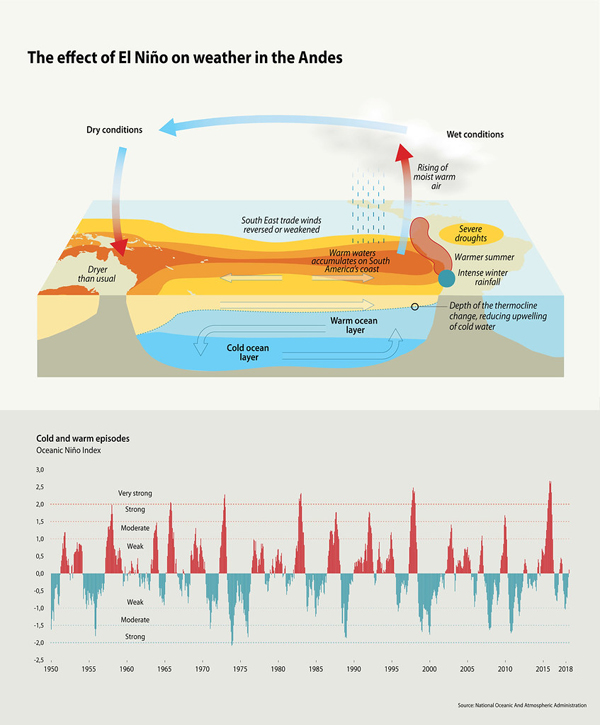
The effect of El Niño on weather in the Andes. Image by Riccardo Pravettoni.
The ENSO is caused by an interaction between the ocean currents and the atmosphere, which changes the temperature of the sea. It can be modelled by an equation very similar to the shower equation. In this case the delay is caused by the time that it takes for the ocean currents to travel from the West coast of South America to the East coast of Asia and then return (see the above figure). This leads to the periodicity that we see. In fact, in this case the equation contains extra nonlinear terms, which lead to chaotic dynamics superimposed on a periodic oscillation.
Our equation is also relevant when it comes to understanding the response of agriculture to climate change. This also involves a delay because crops need time to grow, which makes it hard to plan when to plant and harvest crops in a changing environment.
The shower equation is also, unfortunately, very relevant to our current emergency due to COVID-19. We are trying to control the pandemic through social distancing and vaccinations. But these measures take some time to take effect, so again we are dealing with a delay. In addition, the virus which causes COVID-19 has an incubation period of between five days and two weeks. During this incubation time no symptoms are visible, so there's a delay between a person becoming infected and being visibly sick, which needs to be taken into account when modelling the epidemic. This leads directly to versions of the shower equation, the so-called SIR equations with latency and control, that are used to help us understand, and control, the epidemic. Like with the ENSO system, once delay is built into the equations, things become much more uncertain.
It remains to be seen how controllable the (health and economic) system is as a result.
About this article
This article is based on a talk in Budd's Gresham College lecture series (see video above).

Chris Budd.
Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin, and features in the book 50 Visions of Mathematics ed. Sam Parc.