How to work out doubling time
See here for all our coverage of the COVID-19 pandemic.
With the emergence of the omicron variant, and COVID-19 cases on a steep rise in many European countries anyway, we're back dealing with concepts many of us had hoped we'd left behind. Exponential growth, fast growth rates — and rapid doubling times.
The doubling time of a disease is the time it takes for the number of cases to double. You can calculate the doubling time from the growth rate of the disease, but the relationship is a little more subtle than you might think at first.
A scientifically accurate atomic model of the SARS-CoV-2 virus. Image: Alexey Solodovnikov and Valeria Arkhipova, CC BY-SA 4.0.
For example, for a growth rate of 0.33 (which is roughly what we are seeing in South Africa at the moment) you might think that you have to wait three days for the number of cases to increase by 100%, that is, you might expect a doubling time of three days. But this is not correct. In reality the doubling time is a lot shorter; just over two days. The reason for this is essentially the same as the reason why, if you're not careful, compound interest gets you into debt quicker than you might have thought when you took out the loan.
A little about growth rate
The growth rate of a disease captures how quickly the number of infections are changing day by day. It is modelled using an exponential curve:
![\[ N(t) = c e^{\lambda t} \]](/MI/584d8d7192c1d56eb54882f26881e75f/images/img-0001.png) |
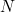is the number of cases, which depends on time 
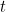measured in days, and 
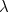(pronounced "lambda") is the growth rate of the disease per day. The number 
is the number of cases at time 
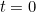, that is, the moment of time you are trying to project forward from.
The number 
is a mathematical constant approximately equal to 2.719. The reason it appears here is that it is intimately connected to growth that is continually compounded. See here for an explanation of the maths behind this, and here for a general explainer of the concept of growth rate.
When you first hear the term "growth rate" you might think that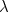 
gives you the increase in cases per day, particularly as it can also be expressed as a percentage. But that’s not quite correct. The day-on-day increase, according to our formula above is
![\[ N(t+1)-N(t) = c e^{\lambda (t+1)}-c e^{\lambda t}, \]](/MI/bab988a28fb7b585b9f3141bda5b3165/images/img-0002.png) |
which simplifies to
![\[ c e^{\lambda t}\left(e^\lambda -1\right). \]](/MI/bab988a28fb7b585b9f3141bda5b3165/images/img-0003.png) |
As a percentage of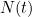 
this is
![\[ \frac{c e^{\lambda t}\left(e^\lambda -1\right)}{c e^{\lambda t}}\times 100 = 100(e^\lambda -1). \]](/MI/bab988a28fb7b585b9f3141bda5b3165/images/img-0005.png) |
Coming back to our example of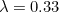 
, we see that the percentage growth per day is not 33%, as you might have thought, but
![\[ 100(e^{0.33}-1)=39\% , \]](/MI/bab988a28fb7b585b9f3141bda5b3165/images/img-0007.png) |
which is quite a bit higher. Only when 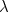is small (say around 
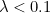) can we take the value of 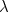itself as an estimate of the day-on-day increase (this is because for these small values 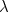is a good approximation of 
).
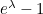Calculating doubling time from growth rate
Now let’s calculate the doubling time from our model of growth rate. We would like to find the length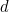 
of the time period it takes for cases to double. Mathematically, we need to solve for 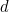the expression
![\[ N(t+d)=2N(t). \]](/MI/a981d7e743cb8227283d295e99cd79d5/images/img-0002.png) |
Using the formula above this means we need to solve for 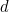the expression
![\[ c e^{\lambda (t+d)}=2 c e^{\lambda t}. \]](/MI/a981d7e743cb8227283d295e99cd79d5/images/img-0003.png) |
Taking logarithms of both sides of the equation gives
![\[ \ln {c}+\lambda (t+d) = \ln {2}+\ln {c}+\lambda t. \]](/MI/a981d7e743cb8227283d295e99cd79d5/images/img-0004.png) |
Solving for 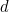gives
![\[ d=\frac{\ln {2}}{\lambda }. \]](/MI/a981d7e743cb8227283d295e99cd79d5/images/img-0005.png) |
This tells us how the doubling time 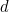depends on the growth rate 
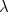. Here is the plot of the relationship. It shows that doubling time does not increase linearly with growth rate, but instead plummets quite dramatically as 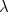increases.
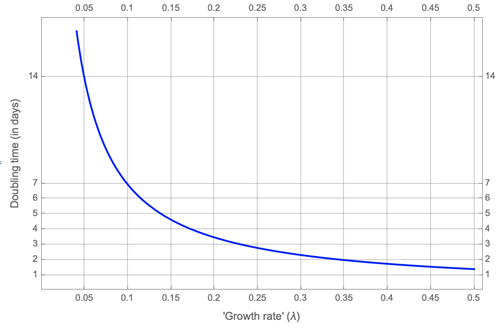
Doubling time in terms of growth rate, as given by the formula we calculated.
Coming back to our example above, for a growth rate of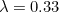 
, our formula tells us that the corresponding doubling time is
![\[ d=\frac{\ln {2}}{0.33} = 2.1, \]](/MI/36236a7d82efdbd7ff6cbf3a126464b4/images/img-0002.png) |
which is just over two days as we claimed.
About this article
Marianne Freiberger is Editor of Plus. This article was produced with Julia Gog, Professor of Mathematical Biology at the University of Cambridge, as part of our collaboration with JUNIPER, the Joint UNIversity Pandemic and Epidemic Response modelling consortium. JUNIPER comprises academics from the universities of Cambridge, Warwick, Bristol, Exeter, Oxford, Manchester, and Lancaster, who are using a range of mathematical and statistical techniques to address pressing question about the control of COVID-19. You can see more content produced with JUNIPER here.
Gog is also a member of SPI-M, a modelling group which feeds its results into the Scientific Advisory Group for Emergencies (SAGE), and of the steering committee of a national consortium, led by the Royal Society, to deal with the COVID-19 pandemic.
