You can read a shorter version of this article here.
June Huh, a mathematician of Princeton University, has won one of this year's Fields Medals at the International Congress of Mathematicians. The Fields Medal is one of the most prestigious prizes in mathematics. It is awarded every four years "to recognise outstanding mathematical achievement for existing work and for the promise of future achievement". Up to four mathematicians up to the age of 40 are awarded a Fields Medal each time.

June Huh. Photo: Lance Murphey.
We were lucky to talk to Huh in the run-up to this year's Congress, which is a fully virtual event event with only the prize ceremonies and lectures taking place in-person in Helsinki, Finland. He told us about his relatively late start in mathematics, and why he enjoys working with maths you can feel and touch.
Not your average mathematician
It's tempting to think of all brilliant mathematicians as prodigies. They excelled at the subject early on, won all the maths prizes at school, and had their path to greatness plotted out before them.
June Huh is refreshingly different. At elementary school his grades in maths weren't great, and highschool got him so bored, he chose to write poetry instead. When he finally did find his way to maths, it wasn't the topic itself that drew him, but a person. Around the time Huh was about to graduate from the Physics and Astronomy course he had ended up taking at Seoul National University, he noticed that the famous mathematician Heisuke Hironaka was giving a lecture course. "I knew nothing about the [mathematics] but I had read Hironaka's autobiography. He's an interesting person, so I enrolled.”"
The course turned out to be a real-time reflection on the research Hironaka was doing at the time, reporting on insights he had literally had the day before. "This was the first time I actually saw someone doing maths," says Huh."It was my first exposure to mathematics as a human activity." And it was the thrill of that human activity that got Huh hooked.
Counting and seeing
See here for all our coverage of the ICM 2022 and the prizes awarded there.
Huh's way of talking about his mathematics is beautifully intuitive. Because he didn't have much maths training, he started his career focussing on objects "visible to the naked eye," as he puts it. "A lot of areas in modern mathematics are so developed, that just to understand the central questions in that area you have to invest several years," says Huh. "It's like studying the kind of astronomy you can only do when you have a million dollar telescope."
An area of maths that's not like this is combinatorics: the art of counting things that lend themselves to being counted, because there are only finitely many of them and they are discrete. A typical question in combinatorics might ask is how many ways there are to order a pack of cards. "All the objects are tangible — you can almost see them and touch them," says Huh. "Combinatorics was the part of mathematics that was visible to my eyes."If counting can be considered a pillar of mathematics — it's one of the first mathematical things we do as children and, as a species, we did at the dawn of humanity — then the other pillar has to be geometry. "Geometry is common to all humans," says Huh. "We are visual creatures, vision is our primary sense organ. We understand the world around us through geometry as opposed to sound, taste or smell."
While you can do a lot of counting without hitting conceptual difficulties, geometry is a little more deceptive. The shape of a knobbly potato is something we immediately get when we see it, but when it comes to describing it without pictures, we are quickly stumped. "Geometry is very hard to formalise," says Huh. "It contains vast amounts of information, especially when you compare it to the complexity of our language and logic."
A sort of miracle occurs, however, when you allow yourself the use of equations. The equation
![\[ y=x, \]](/MI/c1df7d00f00c63d9023a9d908425615a/images/img-0001.png) |
for example, exactly defines a straight line sitting in the plane. The connection comes from equipping every point in the plane with a pair of coordinates 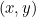 and then marking all points whose coordinates satisfy the equation.
and then marking all points whose coordinates satisfy the equation.
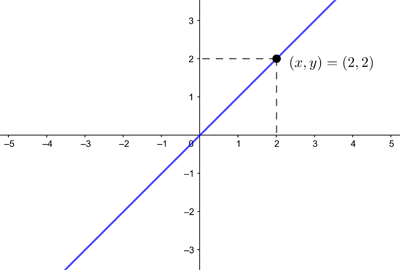
The horizontal line gives the x coordinate of a point and the vertical line gives the y coordinate. The point shown has coordinates (x,y)=(2,2). Every point on the line has coordinates (x,y) that satisfy y=x.
By the same method, and as you might remember from school, the equation
![\[ y = x^2 \]](/MI/21938407fbb0f2ecdb0e88a73bd73878/images/img-0001.png) |
defines a parabola.
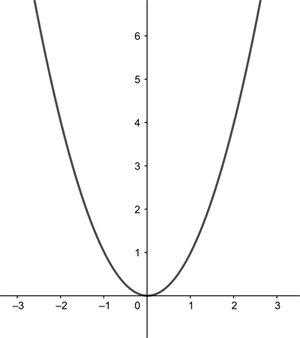
The horizontal line gives the x coordinate of a point and the vertical line gives the y coordinate. The curve shown is the parabola given by the equation y=x2.
Similarly, other equations define other types of shape. Unlike knobbly potatoes, shapes defined by equations can be studied using the tools of algebra. The area of maths which does this is called algebraic geometry.
Polynomials
Huh is talking about polynomial equations which involve sums of powers of the variable  . Formally, a polynomial is defined as
. Formally, a polynomial is defined as
![\[ y=a_ nx^ n+a_{n-1}x^{n-1}+...+a_1x+a_0, \]](/MI/0e69f468b9ec79e0652a9b4a72cac23b/images/img-0002.png) |
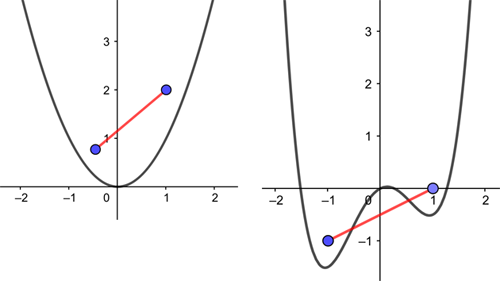
where 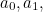 etc up to
etc up to 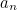 are constants.
are constants.
"In algebraic geometry, in order to specify a [geometric] space, all you have to do is write down an equation, and it's not even a complicated equation." says Huh. (See the box of the right for what kind of equations Huh is talking about.) "You can write it down in your notepad and look at it — it's something you can touch. These are the only kind of spaces I could really put my hands on, at least in the beginning [of my career]. That's why algebraic geometry also appealed to me."
Just one minimum
The maths Huh is being honoured for with a Fields Medal is deep and difficult, involving things we have reported on for prizes awarded at previous ICMs: algebraic varieties and Hodge theory, for example. But when we asked Huh to name a result he was particularly proud of, he pointed to something that can actually be hinted at in simpler terms. It bridges the gap between the continuous and the discrete, and it is also interesting outside of mathematics.
To illustrate the result, we return to the equation of a parabola we already mentioned above:
![\[ y=x^2. \]](/MI/439f28ed23a22e9f8d1d7be6aa97196b/images/img-0001.png) |
An important feature of a parabola is that it's got only one minimal point indicated in blue in the plot below:
The horizontal line gives the x coordinate of a point and the vertical line gives the y coordinate. The curve shown is the parabola given by the equation y=x2. The blue point is a global minimum.
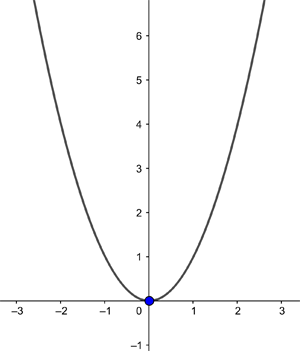
The reason the parabola has just the one minimal point is that the curve doesn’t bulge upwards. That's in contrast to the curve shown below (given by a more complex expression shown in the caption) which has an upward bulge at the bottom that produces two local minima.
The horizontal line gives the x coordinate of a point and the vertical line gives the y coordinate. The curve shown is given by the equation y=x4-2x2+0.5x. The blue points are local minima.
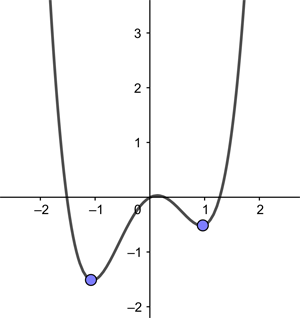
Another way of saying this is that the region above the parabola is convex, while the region above the second curve isn't. (Formally a region is convex, if you can connect any two points that are part of it by a line that is also entirely contained within it.) The function describing our parabola is known as a convex function. The second example is a non-convex function.
The function on the left is convex and the function on the right isn't.

The graph of a convex function of two variables (top) and the graph of a non-convex function of two variables (bottom).
The notion of convexity also exists when there are more than one variable involved in a function — for a function of two variables, it corresponds to a landscape with only a single valley, as opposed to a more complex mountain range. For higher dimensions you can't plot a graph, but the notion of convexity can still be defined.
Finding the optimum
Convex functions are important because many real-life problems involve minimising something. For example, if you're building a car, you want to minimise fuel consumption, which depends on other variables like the car's weight and aerodynamic drag. If you’re given a mathematical function describing the fuel consumption in terms of these variables, then your job is to find a minimum of this function. If you're looking at a complicated function, possibly of many variables, finding this minimum is far from easy to do.
If your function is convex, however, the job becomes a lot easier because convex functions only have one minimal value. It's easy to find this value using techniques that amount to "feeling" your way down: even if you can't see the graph laid out in front of you, you can feel which way is down, go a little way in that direction, and feel again. (These techniques also work when your function has more variables so that you can't draw the graph.)
When it comes to non-convex functions, the feeling around technique can fool you: it may get you to one of several minima, but you can't be sure it's not just as small dip rather than the global minimum you're after.
Building bridges
Convex analysis is invaluable when it comes to optimisation problems. The trouble is, though, that it relies on the objects involved being continuous. If, rather than sitting on a continuous curve, you are sitting on a small island separated from other islands, there's nothing around for you to feel.
"But of course our world is becoming more and more digital [that is, discrete]," says Huh. "Often we want to optimise a certain discrete problem and for this you need very different techniques." Although optimisation researchers have developed a framework to deal with discrete problems, the two areas, until recently, weren't explicitly linked. "The [discrete and continuous] fields are analogous, but there were no straight-foward connections between them," says Huh.
What Huh did in the result he mentioned to us, together with colleagues, is find such a connection through an ingenious change in view point. The equation 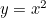 above describes a continuous curve, but is itself defined by a finite amount of discrete pieces of information — that's why we can write it down so easily. All we need to know is what powers of the variables x and y are involved, what the coefficients of these powers are, and where the equal sign goes. You can therefore view the equation as a discrete object.
above describes a continuous curve, but is itself defined by a finite amount of discrete pieces of information — that's why we can write it down so easily. All we need to know is what powers of the variables x and y are involved, what the coefficients of these powers are, and where the equal sign goes. You can therefore view the equation as a discrete object.
Building on this view, Huh and Petter Brändén developed a deep theory that applies to equations known as Lorentzian polynomials. For Lorentizan polynomials, the two views of convexity — one applying to the continuous setting and one to the discrete setting — are naturally linked together through the two different views of the polynomials: as continuous object on the one hand and discrete on the other.
"Finding this formal bridge was very satisfying." says Huh. "And what was even more pleasant for us is that once you have this bridge you can approach problems that were considered very technical and difficult in a very natural and easy way."
Maths as mirror
Great advances in maths often happen when someone makes a connection between seemingly different areas. In some sense, though, Huh doesn't think we should be surprised by those connections. "It's not surprising because the subdivision of [mathematical] areas, or the subdivision of human intuition — combinatorial, geometric, and analytic — are just a result of millions of years of our experience as a species and the kind of sense organs we have. If we were a different kind of creature with a different kind of sense organs and a different kind of environment, we’d presumably have [developed] completely different areas of mathematics."
If the boundaries between the areas of maths are accidental, then it's not surprising that some of the deepest questions in maths transcend them. In that sense, the maths we develop is a mirror of our humanity. "It shows you who we are and how we think."
About this article
Marianne Freiberger and Rachel Thomas, Editors of Plus, interviewed June Huh in June 2022.
This content was produced as part of our collaborations with the London Mathematical Society and the Isaac Newton Institute for Mathematical Sciences. You can find all our content on the 2022 International Congress of Mathematicians here.

