"Mathematics always has a miracle part, the mystical part," the mathematician Szedegy has said. "Somebody works on a problem and suddenly the miracle happens and the new result comes."
Talking about László Lovász, Szedegy adds, "Somehow this miracle happens to him very often."
Today, László Lovász's hand for working miracles is being rewarded with one half of the 2021 Abel Prize, one of the most prestigious prizes in mathematics. The other half of the prize goes to Avi Wigderson (about whom you can read here). The two were awarded the honour for their "fundamental contributions to theoretical computer science and discrete mathematics, and their leading role in shaping them into central fields of modern mathematics."
Early promise

László Lovász. Photo: Hungarian Academy of Sciences/Laszlo Mudra/AbelPrize.
Lovász, born in 1948 in Budapest, showed signs of genius early on in his life. "In the land of prodigies and stars in Hungary, he shone from a very early age," Avi Wigderson has said about his fellow laureate-to-be. Lovász won gold medals in the 1964, 1965 and 1966 International Mathematics Olympiads and even won a prime time Hungarian TV show which had students sitting in glass cages solving maths problems. He went on to study maths at Eötvös Loránd University in Budapest, where he was awarded his PhD in 1970. By that time he was already a significant player on the mathematical scene.
The timing of Lovász's career turned out to be crucial for the contributions he was to make to his field. The digital revolution had not yet happened in the 1970s, but ever since the 1930s people had been thinking about the theory behind computers — trying to figure what kind of tasks a machine might, or might nor, be able to achieve in theory. Since this theoretical aspect of computer science is entirely mathematical, it provided fertile ground for mathematicians at the time. And with computer scientists also making phenomenal progress in developing real computers over the next few decades, Lovász's work came at a time when theory and practice proceeded in harmony.
"I was very lucky to experience one of those periods when mathematics was developing completely together with an application area," he said.
Keeping secrets
Thinking about Lovász's work from today's point of view, perhaps the most striking aspect is its relevance to the online activity we all engage in every day, especially since the pandemic has confined us to our homes. A lot of our online communications need to remain private — we wouldn't want our credit card details, financial transactions, or passwords, to pass through the air in plain sight. Cryptography, the art of encrypting a message so that it can't be read by interceptors, is a crucial component of the digital age. And it's something to which Lovász's work has made major contributions.
There are two things we would want from any scheme for encrypting messages. Encrypting the message should be easy, but decrypting it should be impossible, or at least very, very hard, unless you have the key. Since any message — be it written text, or a picture, or even a video — can be turned into sequences of numbers, encryption schemes usually involve mathematical operations. And in the light of what we've just said, operations that are easy to do and hard to undo provide the perfect candidates.
A good example here is multiplication. While it's easy enough to multiply two numbers, say 5 and 7 to get 5x7=35, if you are given the result, it is that much harder to figure out what its factors are. When the numbers involved are bigger than 5 and 7, then this is even true for computers: they will find it easy to multiply the numbers, but hard to factor the result. This is why the RSA encryption scheme, which is widely used to transmit information securely, is based on multiplication and factoring: encrypting a message involves multiplication, but decrypting it involves factoring. (To find out more about RSA, see this article.)
How hard is hard?
One question that comes up here is, what do we mean by a problem being hard? What's difficult for me might not be difficult for you, and easy for a computer. This question lands us right in the heart of computational complexity, an area that Lovász has made fundamental contributions to.
Computational complexity recognises the fact that many problems get harder as they get bigger. We have already seen this when we talked about factoring numbers above. While factoring a small number, such as 35, is still just about doable in your head, factoring a large number like, say 733763, is a very different story.
Many other problems exhibit this feature. A famous example is the travelling sales person's problem, which requires you to find the quickest route that visits each of a number of cities exactly once (find out more here). Another example involves choosing which of a collection of items to pack into your knapsack so that the knapsack doesn't weigh too much, but the overall value of the items is as large as possible (find out more here). Both problems are easy to solve if there are only a few things involved — cities or items — but get increasingly harder as the number of things grows.
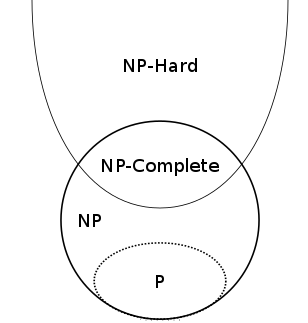
The hierarchy of complexity (assuming the NP class is not equal to the P class). Image: Behnam Esfahbod, CC BY-SA 3.0.
A computer solves problems using an algorithm — a step-by-step recipe. The "bigger" a problem (in the sense we just explained) the more steps the algorithm will have to perform to get to the result. Complexity theorists use this fact to decide how hard a problem is: they look at how the number of steps the algorithm needs to perform grows as the size of the problem grows. If that growth is really fast (e.g. exponential) then the problem is considered hard, and if it grows comparatively slowly, then it is considered easier. In this way, complexity theorists have built up an entire hierarchy of hardness (find out more here).
The problem of factoring numbers and the problem of the knapsack are both thought to belong to a class of hard problems, which is called NP. The travelling salesperson problem is thought to be harder still, belonging to a class called NP-hard. We say "thought to be" because it's still possible that someone, some day, might find ways of solving these problems that are much faster than the ones we know now. Indeed the question of whether the class of NP problems isn't actually as hard as everyone thought is central to one of the most important problems in all of maths: the P vs NP problem (find out more here).
Problems in the NP class have an interesting feature. When they are big enough, they are so hard to crack from scratch that even a computer can't do it within our lifetime or the lifetime or even the lifetime of the Universe. But when you are given a potential solution (e.g. the potential factors of a number) it's easy to find out if it's correct (just multiply them). That's the hard-to-undo but easy-to-do property we noted above.
Three Ls of an algorithm
Coming back to Lovász's work, let's have a look at one of his most famous results, which fits right in with the things we've explored so far: the LLL algorithm, named after Lovász and the brothers Arjen and Hendrik Lenstra.
To see what it's about, imagine a dot on a piece of paper. Draw two arrows starting at that dot. Now also draw the same two arrows, but facing in exactly the opposite direction from the first two. Draw a new dot at the tip of your four arrows.
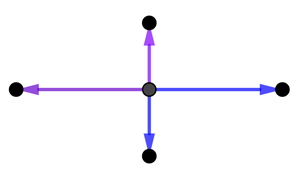
Now draw the same four arrows for each of your new points. This gives you another generation of points at the tips of the new arrows.
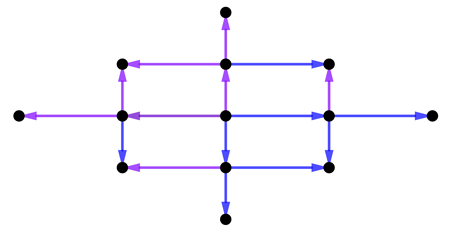
Now do the same for all the new points, drawing four arrows each for the new generation of points. If you keep going like this, you eventually fill your whole page, and if you continue indefinitely in all directions the whole plane, with a grid, called an integer lattice. The pair of arrows which generated this lattice is called the basis of the lattice.
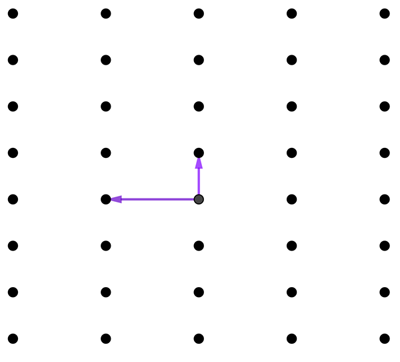
Now it turns out that the same lattice can have different bases. In the example below, two different pairs of arrows give you the same lattice. (Technically the arrows are called vectors).
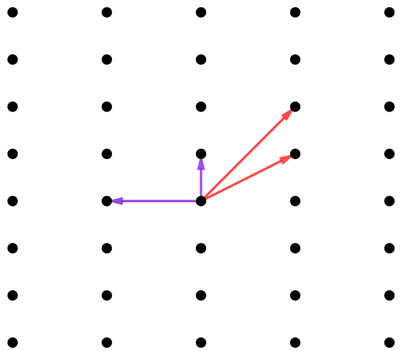
You can also play the game of producing a lattice using vectors in three-dimensional space. And since mathematicians have a way of thinking about the 4th, 5th, 6th, or any higher dimension, they can define lattices and their bases in any dimension.
Now here's a problem: given a lattice (in any dimension), can you find a basis whose vectors are as short as possible (see here for the precise meaning of this) and as close as possible to orthogonal to each other (that is, have right angles between pairs of arrows)?
When we're looking at a lattice in a plane, as in our example, there's an efficient algorithm to solve this lattice reduction problem. But that's not the case when you look at higher-dimensional lattices: the higher the dimension of the lattice, the more steps the algorithms we know have to perform to solve the problem — that's an instance of the problem getting "bigger" as described above. It turns out that, for all known algorithms to solve this lattice reduction problem, the steps needed grows so fast with the dimension of the lattices, that the problem is considered hard — it is probably what is called NP-complete.
You might not think this matters much — because who cares much about integer lattices? But it turns out that many other problems in maths and beyond can be turned into problems concerning integer lattices. This includes problems in number theory, and in something called linear programming which is very useful for solving a large class of real-life problems.
Lovász's visionary contribution to this area was to come up with an algorithm which solves the lattice reduction problem approximately: it may not find you the shortest basis, but it'll find one that, for many purposes, is short enough. Even if the dimensions of the lattices it is applied to get larger, the number of steps needed by the LLL algorithm grows at what's considered a tame rate (in technical terms, it's a polynomial time algorithm). Thus, it gives a "quick" approximate solution to a problem that, in general terms, is really hard.
Cracking and creating secrets
This takes us straight back to cryptography. It turns out that the problem of factoring integers, which is used in RSA cryptography, can also be thought of in terms of lattices. This is why the LLL algorithm has been used to try and attack the RSA cryptosystem: to see if messages encrypted using RSA can't after all be cracked. (This isn't usually done for criminal purposes, but to stress test the method.)

László Lovász. Photo: Hungarian Academy of Sciences/Laszlo Mudra/AbelPrize.
It turned out that, while the LLL algorithm can't crack RSA in general, it can help to crack relaxed versions of the problem where the person trying to crack the code already has some extra information. For example, the mathematician Don Coppersmith showed in 1996 that if a fraction of a message is already known, it might be that the LLL algorithm can help you crack the rest in a feasible (polynomial) amount of time. The exact proportion of the message that needs to be known to decipher the rest in this way depends on the precise numbers used in the RSA encryption. The method of cracking the message is known as the Coppersmith attack.
But this is not all. Cryptographers have used the LLL algorithm, not just to attack existing encryption methods, but also to devise new ones. These are of particular interest. Existing encryption methods such as RSA might be safe right now, due to the difficulty of the maths problems they are based on, but all this may go out of the window when functioning quantum computers arrive in the scene. By contrast, encryption systems based on lattices and the LLL algorithm, are tight to be able to withstand even an attack of a quantum computer.
What we have described here is just the tiniest of glimpses of Lovász's body of work, and a superficial view of the connections between mathematics, theoretical computer science and something that concerns us all — internet security. Another area Lovász has produced important results in concerns the role of randomness in computation. You can read more about this topic in our article on Avi Wigderson's work. To find out more about Lovász more generally, see the MacTutor Website.
But Lovász is not only known for his mathematical prowess. "He's a fantastic advisor and a fantastic teacher, and he has a zillion collaborators," said Wigderson. This mathematical sociability is something Lovász may well have picked up from another mathematical superstar he met early on in his life; Paul Erdős.
We were lucky enough to profit from Lovász's generosity at the 2010 International Congress of Mathematicians, where he talked to us in his role as President of the International Mathematical Union — you can listen to a podcast of this interview here.
Congratulations László Lovász!
About the author
Marianne Freiberger is Editor of Plus.
Comments
Coppersmith Attack
I think you got Don's name wrong: it's Don Coppersmith, not Don Copperfield.
Thanks for pointing that out,
Thanks for pointing that out, we've corrected it!