Mathematical Misfits - three-dimensional
Which fits best in a sphere - a dodecahedron or an icosahedron? That is, if you fit the largest possible dodecahedron and icosahedron inside a given sphere, which leaves least space?

Dodecahedron |

Icosahedron |
(Both images copyright by Rüdiger Appel)
Dual polygons
To solve this puzzle it is useful - although not necessary - to know about dual polygons. Regular dodecahedra and icosahedra are dual to each other. This means that if you take one and put a vertex in place of every face, and a face in place of every vertex, you get the other!
Take the dodecahedron, for example. It has twelve pentagonal faces and a total of twenty vertices, each of which is a vertex of three of the faces. If you put a point at the centre of each face and join together those on adjoining faces, you get twenty equilateral triangle faces, and each vertex is a vertex of five faces - in other words, you get an icosahedron! The reverse works too - you can get a dodecahedron from an icosahedron.
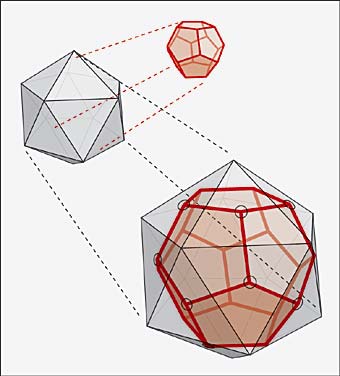
The dodecahedron and icosahedron are dual
The volume of a dodecahedron
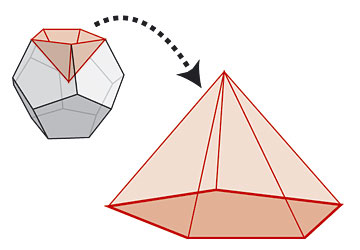
A dodecahedron is 12 of these
We can think of the dodecahedron as a collection of twelve pyramids, each with one of the pentagonal faces as base, and the centre of the dodecahedron as the other vertex. Since the formula for the volume of a pyramid is one-third of the area of the base by the perpendicular height, we need to find both the area of a face and the distance from the centre of a face to the centre of
the dodecahedron. We'll write s for the sidelength of the pentagonal faces.
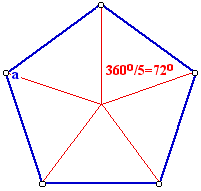
The area of a face
This can be found using simple trigonometry, by noticing which lengths and angles are the same. If we call the angle of the pentagon a, we can quickly see that a=108o, as shown in the diagram to the right.It is not hard to find the distance from the centre of a pentagon to one of its vertices - it is 0.85 times the sidelength. Therefore the distance from the centre of a face of the pentagon to one of the face's vertices is 0.85s. This allows us to find the area of the face - it is five times the area of one of the triangles drawn in the diagram, which each have area
(1/2)(0.85s)s sin(54o) =0.34s2.
Therefore the area of a face is 1.72s2.
The distance from the centre of a face to the centre of the dodecahedron
To find this, we would like to know the sidelength of the equilateral triangle with vertices at the centres of the three faces adjacent to a selected vertex v. This is actually the sidelength of the dual icosahedron inside the dodecahedron - that is, the icosahedron with vertices at the centres of the faces of the dodecahedron.
Finding the sidelength of the dual icosahedron
We do this in three steps.
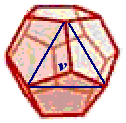
First, consider the equilateral triangle got by joining the three vertices adjacent to v, shown to the right.
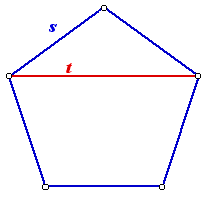
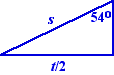
The sidelength of this triangle is t marked on the diagram to the left, and by simple trigonometry using the triangle below, t=1.62s.
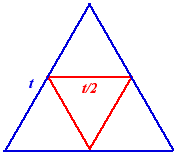
The second step is to move the vertices of this triangle to the midpoints of its sides, which gives the smaller triangle marked to the right in red. The sidelength of this triangle is t/2 = 0.81s.
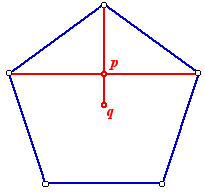
The third step is to move the vertices again so they are at the centres of adjacent faces of the dodecahedron, rather than the midpoints of lines joining the vertices adjacent to v. To do this, we need to move the vertex on each face from the point p shown to the point q. We have already worked out the distance from q to v - it is 0.85s. We can find the distance from p to v - it is 0.59s. Therefore, moving the vertices of the triangle from position p on each face to position q means moving the vertices 0.85/0.59 = 1.44 further away from v, and therefore increasing the sidelength of the triangle by a factor 1.44.
This means that the sidelength of the triangle with vertices at the centres of the faces adjoining  - that is, the sidelength of the dual icosahedron inside the dodecahedron - is
- that is, the sidelength of the dual icosahedron inside the dodecahedron - is 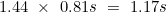 .
.
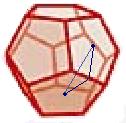
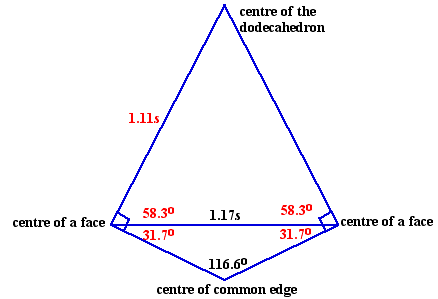
Using the dihedral angle to find the distance between the centres of two faces
Now imagine joining the centres of two faces directly, and also via the midpoint of their common side. It is easy to see that the distance between the centre of a pentagonal face and the midpoint of one of its sides is 0.69s, so the two equal sides of this isosceles triangle will have length 0.69s. Since we know the direct distance between the centres of two adjacent faces, we can easily find the dihedral angle - the angle each face makes with its neighbours - it is 116.6o.
If we use the line joining the two centres as a base for an isosceles triangle with other vertex at the centre of the dodecahedron, the two equal sides make right angles with the faces.
This fact, together with our knowledge of the dihedral angle, allows us to find the internal angles of the triangle, and hence to solve for the equal sides - which are lines joining centre of faces to the centre of the dodecahedron. These have length 1.11s, which is the perpendicular height of the cones based on the faces of the dodecahedron, with other vertex at the centre of the dodecahedron.
Now (finally!) we can calculate the volume of the dodecahedron. The area of a face we know is 1.72s2, the perpendicular height of a cone is 1.11s, so the volume of a cone is
(1.72s2)(1.11s)/3 = 0.64s3,
and the volume of the whole dodecahedron is 12 times this - 7.68s3.
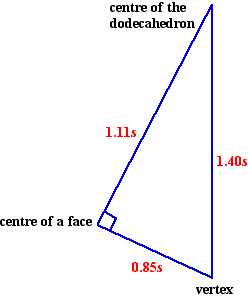
Since we want to know how well it fits inside a sphere, we will also have to calculate the distance from the centre to a vertex, because this will be the radius of the smallest sphere the dodecahedron will fit inside. We can find this distance by using Pythagoras' Theorem to solve the triangle with vertices at the centre of a face, one of its vertices, and the centre of the dodecahedron. It turns out to be 1.40s. The volume of this sphere is then 11.48s3, and the volume of the dodecahedron as a proportion of this volume is 66.9%.
The volume of an icosahedron
This works pretty much the same way, but here's the full solution anyway.We can think of the icosahedron as a collection of twenty pyramids, each with one of the triangular faces as base, and the centre of the icosahedron as the other vertex. Since the formula for the volume of a pyramid is one-third of the area of the base by the perpendicular height, we need to find both the area of a face and the distance from the centre of a face to the centre of the icosahedron. We'll write s for the sidelength of the triangular faces.
The area of a face
Since the faces are equilateral triangles of sidelength s, the area of a face is 0.43s2.
The distance from the centre of a face to the centre of the icosahedron
Proceeding as for the dodecahedron, we would like to know the sidelength of the pentagon with vertices at the centre of the five faces adjacent to a chosen vertex v. This is the sidelength of the dual dodecahedron inside the icosahedron - that is, the dodecahedron with vertices at the centres of the faces of the icosahedron.
Finding the sidelength of the dual dodecahedron
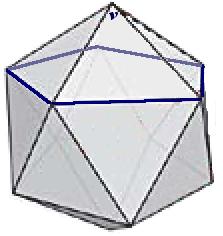
Again, we do this in three steps. First, consider the pentagon got by joining the five vertices adjacent to v. The sidelength of this pentagon is s.
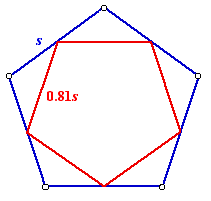
Next we find the sidelength of the smaller pentagon with vertices at the midpoints of the sides of this pentagon. It is easy to find the sidelength of this new smaller pentagon - it is s sin(54o)=0.81s.
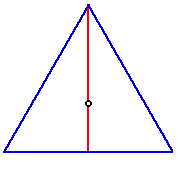
The third step is to move the vertices from the midpoints of the edges opposite to v to the centres of the faces adjoining v. This is easy, because the centre of an equilateral triangle - marked in the diagram to the left in black - divides the perpendicular joining a vertex and the midpoint of the opposite side - marked in red - in the ratio 2:1, so in moving the vertices we decrease the size of the pentagon to two-thirds what it was, and its sidelength becomes 0.54s. This is the sidelength of the of the dual inscribed dodecahedron, that is, the distance between the midpoints of two adjacent faces of the icosahedron.
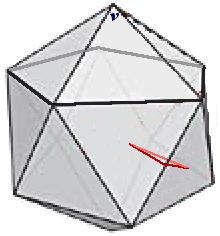
Now we can find the dihedral angle of the icosahedron, using the triangle with vertices at the centre of two adjoining faces of the icosahedron, and the midpoint of their shared edge. This is an isosceles triangle with two edges of length 0.29s and the other of length 0.54s. We find that the dihedral angle of the icosahedron is 137.2o.
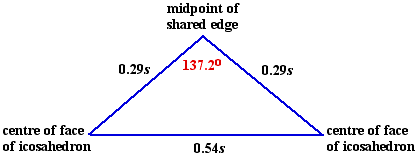
If we use the line joining the midpoints of adjacent faces as a base for an isosceles triangle with other vertex at the centre of the icosahedron, the two equal sides make right angles with the faces.
This fact, together with our knowledge of the dihedral angle, allows us to find the internal angles of the triangle, and hence to solve for the equal sides - which are lines joining centre of faces to the centre of the icosahedron.
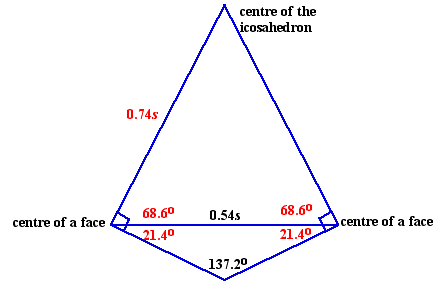
Now we can calculate the volume of the icosahedron. The area of a face we know is 0.43s2, the perpendicular height of a cone is 0.74s, so the volume of a cone is
(0.43s2)(0.74s)/3 = 0.11s3,
and the volume of the whole icosahedron is 20 times this - 2.2s3.
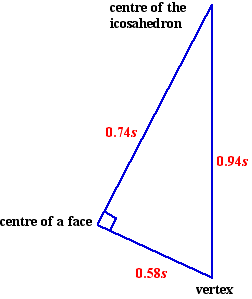
Since we want to know how well it fits inside a sphere, we will also have to calculate the distance from the centre to a vertex, because this will be the radius of the smallest sphere the icosahedron will fit inside. We can find this distance by using Pythagoras' Theorem to solve the triangle with vertices at the centre of a face, one of its vertices, and the centre of the icosahedron. It turns out to be 0.94s. The volume of this sphere is then 3.47s3, and the volume of the icosahedron as a proportion of this volume is 63.4%.
The home stretch
The dodecahedron fits better, because it takes up 66.9% of its sphere, whereas the icosahedron can only manage 63.4%!Back to main puzzle page
What?!
Please do a more thorough proof. I've been working on this problem for days. I can't spot any mistakes in my work, but my answer is wrong. I just want a dihedral angle proof for the dodecahedron. less words more trig!
percentages
I come up with different percentages. 60.546% for the icosahedron and 66.49% for the dodecahedron.