Worms
Bored with Sudoku? Try this version with added worms:
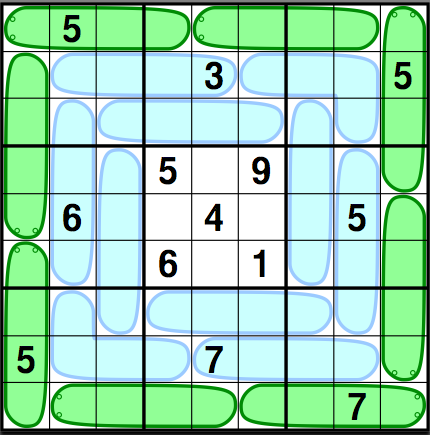
Here are the rules:
Fill in the grid like a Sudoku puzzle; that is, so that the numbers 1, 2, 3, 4, 5, 6, 7, 8, and 9 each appear exactly once in each row, column, and 3 × 3 block. In addition, there should be no repeated entries in any "worm", and each worm should consist of an increasing sequence of numbers from tail to head. For example, a worm of length four could contain the numbers 2, 5, 6, and 8, in that order from tail to head. Green worms have their heads marked with "eyes", but blue worms don't — so you have to figure out their direction yourself. Have fun!
This puzzle was kindly provided by Brainfreeze puzzles, a puzzle making company run by the mathematician Laura Taalman and the software developer Philip Riley, whose book Color Sudoku will be available in the spring.
If you are stumped by last issue's puzzle, here is the solution.
For some challenging mathematical puzzles, see the NRICH puzzles from this month or last month.