This article is the winner of the schools category of the Plus new writers award 2006.
Dice are invaluable to many games, especially gambling games, but instead of playing with ordinary 1-6 numbered dice here are two interesting alternatives — with a twist!

Welcome to the Maths Casino!
Sicherman Dice
No doubt you are familiar with rolling a pair of dice and summing the spots — take Monopoly for example. But is there a different pair of dice that will still give a fair game? This was the problem conceived and solved by Colonel George Sicherman in the 1970s.
| + | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Sicherman aimed to find a different pair of six sided dice with positive integer face values, with the same probability distribution as a pair or ordinary dice. Having the same probability distribution ensures you still have the same chance of achieving a certain score.
| Possible scores | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Probability that you will roll that score | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
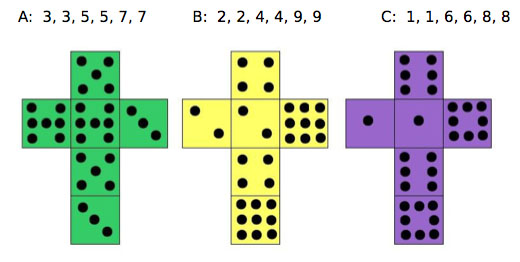
There is one such pair of dice — Die 1 with faces 1, 2, 2, 3, 3, 4 and die 2 with faces 1, 3, 4, 5, 6, 8 — but how did Sicherman find it?

Sicherman Dice
The answer lies in expressing a die as a polynomial. (A polynomial is an expression with terms involving a variable, x, raised to different integer powers). For each term in the polynomial, the power of x represents the face value and the coefficient the number of faces with that value.
An ordinary die would therefore be expressed:
![\[ x^6 + x^5 + x^4 + x^3 + x^2 + x \; \; \; \; \; \; \mbox{(A)} \]](/MI/2cb47527cec96e64e7278e92320a5bf9/images/img-0001.png) |
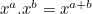 , and
, and  and
and 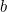 represent the face values of the dice). So the polynomial for the sum of two ordinary dice is
represent the face values of the dice). So the polynomial for the sum of two ordinary dice is 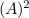 :
: ![\[ ( x^6 + x^5 + x^4 + x^3 + x^2 + x )^2 = \]](/MI/2cb47527cec96e64e7278e92320a5bf9/images/img-0006.png) |
![\[ x^{12} + 2x^{11} + 3x^{10} + 4x^9 + 5x^8 + 6x^7 + 5x^6 + 4x^5 + 3x^4 + 2x^3 + x^2 \; \; \mbox{(B)} \]](/MI/2cb47527cec96e64e7278e92320a5bf9/images/img-0007.png) |
The polynomial obtained is in fact an expression of the probability distribution of rolling two dice. It is easy to see that if a term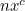 appears in the product (B), then there are exactly
appears in the product (B), then there are exactly 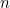 combinations of rolls that give you the sum
combinations of rolls that give you the sum  , and vice versa. (Out of the 36 possible rolls, there are one 12, two 11's, three 10's, four 9's, five 8's, six 7's, five 6's, three 4's, two 3's, and one 2.) So multiplying the polynmoials corresponds to considering the sum of two rolls.
, and vice versa. (Out of the 36 possible rolls, there are one 12, two 11's, three 10's, four 9's, five 8's, six 7's, five 6's, three 4's, two 3's, and one 2.) So multiplying the polynmoials corresponds to considering the sum of two rolls.
To find the Sicherman Dice an alternative pair of factors for (B) must be generated. So we need to consider the following constraints:
- Faces cannot be blank so the generated pairs cannot have
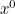 terms (
terms (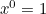 ) .
) . - The dice have six faces so the coefficients must add to six.
(This can be checked by setting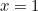 and as
and as 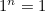 the answer should be 6.)
the answer should be 6.) - All factors of (B) must be included in the alternative pair of factors.
To begin factorising (B), let us first consider factorising (A) and then simply square our answer:
 |
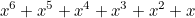 |
|||
 |
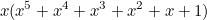 |
|||
 |
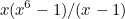 |
|||
 |
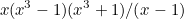 |
|||
 |
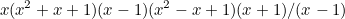 |
|||
 |
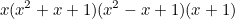 |
Therefore factors of (B), 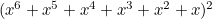 , are:
, are:
![\[ x^2 (x^2 + x + 1)^2 (x^2 - x + 1)^2 (x + 1)^2 \; \; \; \; \mbox{(C)} \]](/MI/fe6c744f0c5f77d4e6955ca126120e2b/images/img-0002.png) |
Valid pairs of dice can now be found by splitting (C) into pairs of polynomials. In (C) we have two  factors, two
factors, two 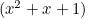 factors, two
factors, two 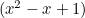 factors, and two
factors, and two 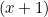 factors. And we can use any combination of these that obeys the constraints.
factors. And we can use any combination of these that obeys the constraints.
To get no 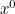 terms, both of the polynomials in the pair must contain one of the
terms, both of the polynomials in the pair must contain one of the  factors. (Otherwise we will be left with "1" from multiplying out the other brackets.)
factors. (Otherwise we will be left with "1" from multiplying out the other brackets.)
To ensure we have each die with six faces, both of the polynmoials must equal 6 when 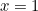 . And to have this value of 6 each polynmoial must contain a factor equal to 3, and a factor equal to 2 when
. And to have this value of 6 each polynmoial must contain a factor equal to 3, and a factor equal to 2 when 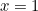 . This corresponds to both of the polynomials having an
. This corresponds to both of the polynomials having an 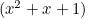 and an
and an 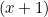 factor.
factor.
In fact these constraints only leave the two 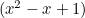 factors to play with! There are two potential combinations:
factors to play with! There are two potential combinations:
Combination A:
Die 1: 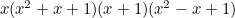
Die 2: 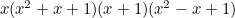
When multiplied out these are the ordinary dice.
Combination B:
Die 1: 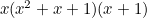
Die 2: 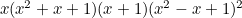
And multiplying these out we get the polynomials for the Sicherman Dice:
Die 1: 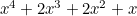
Die 2: 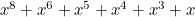
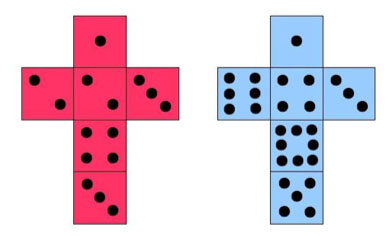
Nets of Sicherman's Dice
| + | 1 | 2 | 2 | 3 | 3 | 4 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 3 | 4 | 4 | 5 |
| 3 | 4 | 5 | 5 | 6 | 6 | 7 |
| 4 | 5 | 6 | 6 | 7 | 7 | 8 |
| 5 | 6 | 7 | 7 | 8 | 8 | 9 |
| 6 | 7 | 8 | 8 | 9 | 9 | 10 |
| 8 | 9 | 10 | 10 | 11 | 11 | 12 |
An interesting point to note is that sums of the opposite sides are 5 and 9 respectively which averages to 7, the sum of the opposite sides on a normal die.
And, as sought, our probability distribution is the same as for a pair of ordinary dice.
| Possible scores | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Probability that you will roll that score | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
By changing the constraints similar sets of dice can be investigated using the same method. If blank sides are allowed we can play around with the x factor to find two other pairs of Sicherman-like dice.
And the dice need not be six sided, any platonic solid may be used. (Arguably any solids at all could be used, but many would have an irregular weight distribution and be biased dice.) Generally as the number of faces on the die and terms in the polynomial increases there are more viable pairs of dice. For example, an octahedron has three combinations and a dodecahedron thirteen. However this is not always the case, a 35 sided shape again has only one pair!
You might like to take the problem one stage further:
- Could the same method be used for triplets of dice?
- By starting with any probability distribution and expressing it as a polynomial could dice then be found to give that distribution?

A non-transitive game: scissors beat
paper and paper beats rock, but
scissors are no match for rock
Efron's Dice
Now we play a different game with another set of unusual dice. They were invented by Bradley Efron, a statistician at Stanford University, California.
The game now consists of two players picking one of three dice and rolling it, with the highest score winning. Efron's Dice have interesting probability properties. They are non-transitive. This means that although die A beats die B, and die beats die C, die C beats die A! This is somewhat counterintuitive but think of the playground game "Rock, Paper, Scissors", perhaps a more familiar non-transitive situation.
But what are the dice?
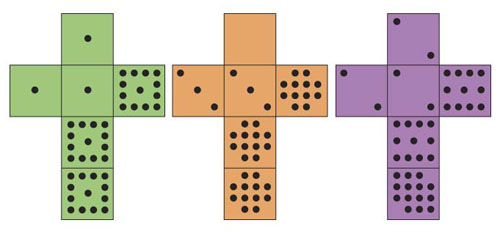
Nets of Efron's Dice
Looking at a wins/losses table, the non-transitive nature of these dice can easily be seen:
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In fact the probability of A beating B, B beating C, and C beating A is always 20/36 = 5/9.
Therefore the winning strategy is simple: let your opponent pick their dice first then pick its superior. For example if they choose A, you choose C.
| 6 | 1 | 8 |
| 7 | 5 | 3 |
| 2 | 9 | 4 |
It is interesting to note that arranging the values of these dice can make a magic square. The three values of each die are all placed in the same row or column and when correctly arranged the rows, columns and diagonals will all have a total of fifteen.
Efron also designed three sets of four die which are also non-transitive.
|
|
|
||||||||||||||||||||||||||||||
Again the wins/losses tables can be used to verify this and find the probability of winning. For Set 1:
P(A>B) = P(B>C) = P(C>D) = P(D>A) = 2/3
where P(A>B) means the probability of A beating B.
Of course, now we have 4 dice there are other combinations which are not covered in the above combinations. We could also trying playing A against C, or B against D.
| Using Set 1 again: | P(A>C) = 4/9 |
| P(B>D) = 1/2 (the same as ordinary dice) |
Okay, so using Efron's Dice , to have the upper hand your opponent must choose first. However what if you have to choose first? Fascinatingly, with a set of three dice found by Allen Schwenk, from Western Michigan University, if you change the rules of the game slightly the probability switches and you again have the advantage.
Schwenk's Dice
Nets of Schwenk's dice
| A: 1, 1, 1, 13, 13, 13 | B: 0, 3, 3, 12, 12, 12 | C: 2, 2, 2, 11, 11, 14 |
Firstly considering Schwenk's Dice normally with one roll, you can calculate the wins/losses tables to see that:
P(A>B) = P(B>C) = P(C>A) = 7/12
So in the game if you have had to pick first, say you picked die B, a clever opponent might pick die A, as this has an advantage over your die when playing with just one roll. But you can still turn the tables by changing the rules of the game: now you and your opponent compete with the total of two rolls (both with your chosen die).
To find your winning chances with the total of two rolls we must find the probability distribution for each dice and its possible totals.
| Die A | ||||||
|---|---|---|---|---|---|---|
| + | 1 | 1 | 1 | 13 | 13 | 13 |
| 1 | 2 | 2 | 2 | 14 | 14 | 14 |
| 1 | 2 | 2 | 2 | 14 | 14 | 14 |
| 1 | 2 | 2 | 2 | 14 | 14 | 14 |
| 13 | 14 | 14 | 14 | 26 | 26 | 26 |
| 13 | 14 | 14 | 14 | 26 | 26 | 26 |
| 13 | 14 | 14 | 14 | 26 | 26 | 26 |
The possible totals for two rolls of Die A of Schwenk's Dice, and the probability table for those scores.
| a | 2 | 14 | 26 |
|---|---|---|---|
| P(A=a) | 1/4 | 1/2 | 1/4 |
| Die B | ||||||
|---|---|---|---|---|---|---|
| + | 0 | 3 | 3 | 12 | 12 | 12 |
| 0 | 0 | 3 | 3 | 12 | 12 | 12 |
| 3 | 3 | 6 | 6 | 15 | 15 | 15 |
| 3 | 3 | 6 | 6 | 15 | 15 | 15 |
| 12 | 12 | 15 | 15 | 24 | 24 | 24 |
| 12 | 12 | 15 | 15 | 24 | 24 | 24 |
| 12 | 12 | 15 | 15 | 24 | 24 | 24 |
The possible totals for two rolls of Die B of Schwenk's Dice, and the probability table for those scores.
| b | 0 | 3 | 6 | 12 | 15 | 24 |
|---|---|---|---|---|---|---|
| P(B=b) | 1/36 | 1/9 | 1/9 | 1/6 | 1/3 | 1/4 |
| Die C | ||||||
|---|---|---|---|---|---|---|
| + | 2 | 2 | 2 | 11 | 11 | 14 |
| 2 | 4 | 4 | 4 | 13 | 13 | 16 |
| 2 | 4 | 4 | 4 | 13 | 13 | 16 |
| 2 | 4 | 4 | 4 | 13 | 13 | 16 |
| 11 | 13 | 13 | 13 | 22 | 22 | 25 |
| 11 | 13 | 13 | 13 | 22 | 22 | 25 |
| 14 | 16 | 16 | 16 | 25 | 25 | 28 |
The possible totals for two rolls of Die C of Schwenk's Dice, and the probability table for those scores.
| c | 4 | 13 | 16 | 22 | 25 | 28 |
|---|---|---|---|---|---|---|
| P(C=c) | 1/4 | 1/3 | 1/6 | 1/9 | 1/9 | 1/36 |
The wins/losses tables for the game (competing with a total of two rolls) are again constructed with these possible totals. For example, the game of die A against die B is won or lost as follows:
| Die A | ||||
|---|---|---|---|---|
| D i e B |
2 | 14 | 26 | |
| 0 | W | W | W | |
| 3 | L | W | W | |
| 6 | L | W | W | |
| 12 | L | W | W | |
| 15 | L | L | W | |
| 24 | L | L | W | |
However care must be taken interpreting this table as the probability of achieving the values for die A and B are no longer equal. The probability of die A winning therefore is not the easy answer of 11/18, but is instead the sum of the different probabilities for each win.
We write each winning combination in the form P(a,b) (where a and b are a possible value of dice A and B respectively).
P(2,0) = P(A=2) x P(B=0) = 1/4 x 1/36 = 1/144
P(14,0) = P(A=14) x P(B=0) = 1/2 x 1/36 = 1/72
P(26,0) = P(A=26) x P(B=0) = 1/4 x 1/36 = 1/144
P(14,3) = P(A=14) x P(B=3) = 1/2 x 1/9 = 1/18 ...
When the probabilities of all the winning combinations are summed P(A>B) is produced, and as expected, B now does have marginally better chances of beating A. By using the same technique (you do get quite quick at it) the probabilities of C now beating B and A beating C can be established.
So both Efron's and Schwenk's dice give you an advantage when your opponents has to pick their die first. But only Schwenk's dice, along with a little tweaking of the game, gives you an advantage if you have to take first pick. But what would happen if you changed the rules and rolled Efron's Dice twice? And, with Schwenk's dice, who will have the advantage with three rolls, or four, or, for the very brave, n rolls?
These are just a few examples of mathematics in the gaming world, and there are many other dice and dicing games in existence with interesting irregularities, try a little internet browsing! Undoubtedly there are also plenty yet to be designed which, as these dice demonstrate, only requires some basic mathematics. Therefore finding them is potentially an open opportunity for all, as it just requires an imaginative mind and some spare time.
About the author

Clare Hobbs is currently in the upper sixth at St. Leonard's School, Durham, and studying Double Maths, Geography and Physics. She intends to study Maths at University, hopefully Cambridge, with a view to pursuing a career in research. Clare was introduced to Sicherman Dice this summer on a week's work experience at Durham University.
"To me maths is a subject that spans across space and time - essential to our understanding of both fundamental particles and the shape of the universe; and as prevalent in ancient civilisations as in modern technology!"