On a clear day: solution
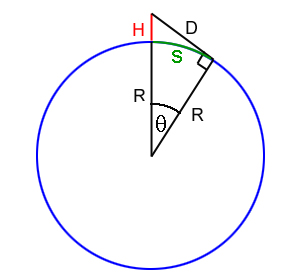
R is the radius of the Earth, H is your height and D is how far you can see. The walking distance across the Earth's surface is the length of the arc s.
Solution to problem 1: In Issue 54's Outer Space [maths]you were asked to work out the "walking" distance over the Earth's surface to the horizon. This is equal to the length $s$ of the arc of the circle from the point where you are to the point where your line of sight hits the surface of the Earth, which is $$s=R\theta$$ where $\theta$ is the angle as shown in the diagram and $R$ is the radius of the Earth. Now bearing in mind that we have a right-angled triangle we have $$\cos{\theta}=R/(R+H),$$ so $$s=R\cos^{-1}{(R/(R+H))}.$$[/maths] [maths]If $R$ is much larger than $H$ then the straight line distance to the horizon is approximately equal to $\sqrt{2HR}$, as we worked out in the article. Moreover, in this case the straight line distance is approximately equal to the walking distance over the Earth's surface. This gives that for $R>>H$ $$R\cos^{-1}(R/(R+H)) \approx \sqrt{2HR}.$$[/maths]
Solution to problem 2: You see something, like a cloud or a hot air balloon, high in the sky beyond the horizon and you know its maximum possible height above the ground. Can you work out how far away it could be?
[maths]Let's assume that the object is at the maximum possible height $h$ above the surface of the Earth. So in our two-dimensional view it lies somewhere on the circle of radius $R+h$ about the centre $O$ of the Earth. Since it is beyond the horizon, the object lies beyond (from your point of view) the straight line through $O$ and the horizon point $P$. And since it is visible over the horizon, the object lies "above" the tangent line passing through your view point and the horizon point $P$. Thus the object lies somewhere on the arc of the circle between points $A$ and $B$ (see the diagram on the right).[/maths]
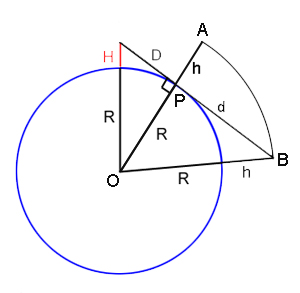
[maths]Using Pythagoras' theorem, we see that the distance from you to point $A$ is $$\sqrt{D^2+h^2}.$$ We have already worked out that for a person of height $H=1.8m$, we have $D=\sqrt{2RH}=4800m,$ and we know that $R=6400km.$ So for a maximum height of $h=2km$ we get that the object is at least $5.4km$ away from you.[/maths]
[maths]Now let $d$ be the distance from $P$ to $B$. Using Pythagoras' theorem on the right-angled triangle $OPB$, we get $$d^2+R^2=(R+h)^2.$$ Noting that $R > > h$, so that we can ignore the $h^2$ term, we have $$d \approx \sqrt{2Rh}.$$ Now the maximum distance to the object from the observer is approximately equal to $$D+d=\sqrt{2HR}+\sqrt{2Rh}.$$ Using $D=\sqrt{2RH}=4800m$, $R=6400km,$and $h=2km$ we get that the maximum distance to the object is approximately $164.8km.$[/maths]