
Give me a dollar and I'll go away
The world is holding its breath at the moment, faced with a potential bird flu pandemic that could kill millions of people. To combat threats like this we need to understand how infectious diseases spread. While it's important to explore the biological processes behind transmission of diseases and mutation of viruses, mathematical research is equally essential: can we find a mathematical model describing people's interactions and the way they move around?
The latter question is now a good deal closer to an answer, thanks to an internet game which tracks the movement of dollar bills. The website http://www.wheresgeorge.com allows you to register your favourite dollar bill and then monitor its progress throughout the US. When Dirk Brockmann, a postdoctoral fellow at the Max Planck Institute for Dynamics and Self Organization, came across this site he immediately spotted its potential: bank notes travel with people, so the site is a gold mine in terms of travel data. "Since we can't track people with tracking devices, like we do animals, we needed to get data that provided us with millions of movements of individuals," explained Lars Hufnagel, Brockmann's co-author from the Kavli Institute for Theoretical Physics at the University of California, Santa Barbara. "We recognized that the enormous amount of data, as well as the geographical and temporal resolution of bill-tracking, allowed us to draw conclusions about the statistical characteristics of human travel, independent of which means of transportation people use," adds Brockmann.
Together with Theo Geisel, director of the Max Planck Institute for Dynamics and Self Organization and professor at the University of Göttingen, the two set out to investigate the data and came up with a surprisingly simple model that only depends on two parameters.
The researchers used the data to estimate the distribution of the probability P(r) that a single dollar bill travels distance r within a time span of 1-4 days. They found that this distribution behaves like a power law: for r larger than 10km, it is very similar to the function
with β being a value close to 0.6.
As you can see, this function decreases as r grows larger, meaning that long journeys are less common than short ones — as you would expect. However, it does not decrease as fast as other common probability distributions, and this means that long journeys still are common enough to have a significant effect on the overall travel behaviour of the notes. Dollar bills make many short journeys, but the occasional long haul ensures that they disperse widely.
However, a mathematical model based solely on the distribution P(r) proved to be way off the mark. It predicted that bills should spread to various locations in the US faster than they actually did. Something else had to be holding them back.
The clue came from the team's estimation of the probability φ(t) that a bill spends time t resting in one place before moving on. Again, they found that the distribution follows a power law
with α close to 0.6, meaning that long resting periods have a strong effect and stop bills from diffusing too quickly.
Equipped with the two distributions, the researchers modelled the bills' progress as a random walk: an individual bill takes a series of random trips, spending a random amount of time at rest between journeys. The probability that it travels distance r in one trip is P(r) and the probability that it's at rest for time t is φ(t). This random walk recipe comes up with a relatively simple function describing the journeys, which only depends on α and β.
This time, the model stood up to scrutiny: it predicted the actual travel patterns as recorded by the website remarkably well; the agreement of simulated and actual data was, according to the team's article in the journal Nature, "very satisfactory". With the values for α and β that come from the data, both around 0.6, the model predicts that the bills disperse quite quickly, though slightly held back by the long waiting times.
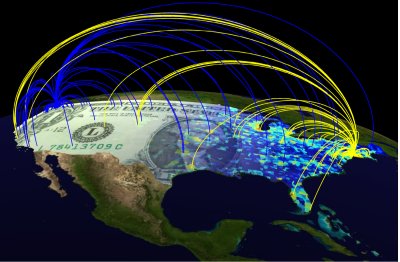
Each line in this illustration symbolizes the geographic movement of a single U.S. dollar bill from either Seattle (blue) or NewYork (yellow) to various destinations in the country. The bills travelled for less than a week.
But how do we know that bills really do travel like people? Couldn't they be slowed down by long periods sitting in a bank? The researchers have theoretical reasons why they believe the behaviour of people and bills is indeed similar, and their opinion is backed up by human travel data from the United States aviation network and the International Air Transport Association.
The fact that the model is so universal is good news: not only does this make calculations easier when the model is used, but simple models can also be an indication that the theorists are on the right track. Nature seems to prefer simplicity. "What is amazing about these particular scaling laws," says Hufnagel, "is the fact that they are determined by two universal parameters only. This result surprised us all."
Further tests will show whether the model does indeed hold up in the long run. If it does, then, according to Geisel, this "will drastically improve predictions about the geographical spread of epidemics."