Given an 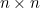matrix 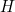and a vector 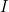of length 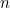, their product 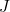is also vector of length 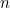(strictly speaking we should write 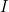as a column vector here). The first entry of 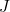is the sum:

	the first entry of the first row of ×  the first entry of
+	the second entry of the first row of ×  the second entry of
+	...
+	the last entry of the first row of ×  the last entry of .

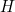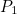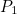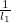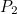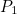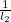Now recall how we have built the matrix . The first row records the information on back links of the page : the first entry of this row is zero if does not link to itself and if it does, the second entry of the first row is 0 if does not link to and if it does, etc. Here the 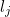are the total number of links on page 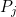. Now each entry of the first row of 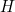is multiplied by the corresponding entry of the importance vector 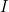. So the first entry is multiplied by the importance of 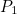, to get either 0 or 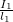. The second entry is multiplied by the importance of 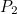to get either 0 or 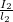, etc. Putting all this together shows that the first entry of the vector 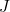is equal to the sum of the importance of the pages that link to page 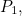weighted by the total number of links on those pages. This is precisely what we defined the importance of page 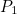to be. So the first entry of 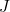is equal to the first entry of the importance vector 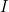. The second entry of 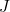is the sum:

	the first entry of the second row of ×  the first entry of
+	the second entry of the second row of ×  the second entry of
+	...
+	the last entry of the second row of ×  the last entry of .

Again we see that the second entry of 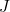is equal to 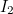, the second entry of the importance vector 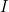. The multiplication carries on correspondingly for each row of 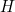, and this shows that .

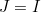Return to article