
Analemmatic sundials: How to build one and why they work
Introduction
Imagine that you have just got the latest in digital watches, with a stop watch, date, times from all over the world, and the ability to function at 4000 fathoms. There is just one small problem: the batteries have gone flat. However, if the sun is shining you don't need to use a watch at all, because the sun makes an excellent clock which (fortunately) doesn't need batteries that can run down. This article is all about a particular kind of sundial and how you can build one for yourself.
IMPORTANT SAFETY ADVICE
Never look directly at the sun!
We often take the problem of telling the time or of finding the day's date for granted, but finding solutions to both of these questions is vital to our civilisation. Early men and women needed to have an accurate notion of the seasons in order to know when to plant and harvest their crops. As civilisation developed it became important to know the time during the day. Two times were obvious as everyone was aware of when the sun rose (dawn) and when it set (dusk). More accurate observations of the sun then showed that having risen in the East, it climbed to its highest point in the sky (due South in the Northern hemisphere) before descending towards its setting point in the West. The time of the highest point reached by the sun (which is when the shadows were shortest) is called Noon. Knowing dawn, Noon and dusk gave us morning, afternoon and night.
Every civilisation has been interested in the way the sun moves, and astronomy and mathematics have always developed alongside each other. Better observations called for quicker and more efficient mathematical methods. More detailed theory drove people to make more accurate observations. In this way both theory and practice evolved together. In this article we give some theory about the way the sun moves and then concentrate on a practical method for building a type of sundial known as an analemmatic sundial. We choose initially not to give too much justification for the mathematics behind the construction of this dial. Details of the theory of this dial can be found in a later section of this article.
Note that the following article assumes that you are in the Northern Hemisphere. If you want to build a sundial that is to work South of the equator you will need to make some changes, but the following method is easy to adapt.
What is an analemmatic sundial?
An analemmatic sundial is a particular kind of horizontal sundial in which the shadow-casting object is vertical, and is moved depending on the date, or to be more precise, depending on the declination of the sun on a given day. The time is read from the dial by noting where the shadow cast by the vertical pin crosses hour points laid out on an ellipse. If we make the dial on the ground and large enough, we can use the shadow cast by a person. This makes it very different from the traditional sundial we see often in parks and gardens where the shadow is cast by a triangular shaped wedge. The analemmatic sundial is perfect as a piece of large mathematical sculpture.
| Traditional Dial | Analemmatic Dial | |
 |
 |
|
| Shape | Hour lines radiate from a central point. | Ellipse of hour points. |
| Shadow-casting object | Fixed, parallel to Earth's axis. | Changes daily, vertical. |
What is the declination of the sun?
Before we can construct our dial we need to understand what the "declination of the sun" is. Look at figure 1, showing the Earth as seen from the side. Imagine you are standing on the surface of the Earth at the point $P$. Your latitude, i.e. your angular distance from the equator, is marked as $\phi$. The diagram shows the situation at Noon so the sun is at its high point for the day and will appear to be due South from where you stand.
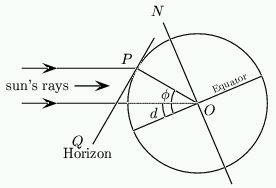
Figure 1: Calculating the declination of the sun.
| {\bf Exercise 1:} Using this diagram, show that the angle $\psi$ that the sun makes with the horizontal at Noon is \setcounter{equation}{0} \begin{equation} \psi = d + 90 - \phi \end{equation} Calculate this for your own latitude at mid-summer and mid-winter. |
On any given day the declination of the sun, marked as $d$ in figure 1, is the angle the rays of the sun make with the plane of the equator of the Earth. Because the axis of the Earth is tilted and we rotate around the sun, this angle changes during the year. It is this change that gives us the seasons. \par In the Northern hemisphere, $d$ is positive in summer, and at the spring and autumn equinoxes the sun is directly overhead at the equator at Noon so $d=0$. At the summer solstice $d=23.5^o$, and at the winter solstice $d=-23.5^o$. As the latitude of the equator is $\phi=0^o$ the formula $\psi = d + 90 - \phi$ above gives $d=0$. A graph of average values is shown in figure 2 and the average values for the first day of each month are in table 2.
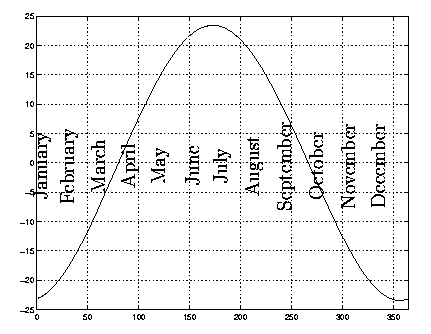
Figure 2: The declination of the sun.
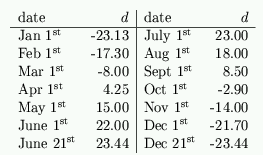
Table 2: Average values of the declination of the sun.
The path that the sun appears to trace in the sky during the day is a {\em circle}. Of course part of this circle will be below the horizon during the night! The centre of this circle is a point due North at an angle $\phi$ to the horizontal.
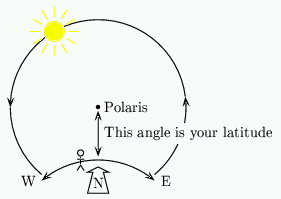
Figure 3: The path of the sun.
This point is marked (to a very good approximation) by the pole star Polaris. The angle between the sun and Polaris is simply $90^o-d$.
In a normal sundial, a shadow is cast by a "gnomon" or pointer that points directly towards Polaris. If a disc of card is stuck to this pointer, perpendicular to it, then the shadow cast by the sun is of constant length throughout the day and moves around the card clockwise with the end point of the shadow lying on a circle. Such a sundial (called an equatorial sundial) is very easy to make and you can see one in figure 4. By seeing where the shadow falls we can tell the time.
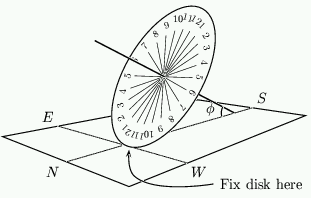
Figure 4: The completed equatorial sundial.
In an analemmatic sundial the pointer is vertical. The shadow cast by the sun on a horizontal surface, such as the ground, moves clockwise around the pointer, but this time it varies in length during the day. The endpoint of the shadow no longer falls on a circle. Indeed, when the sun sets, the shadow is of infinite length. We can still tell the time from the position of the shadow, but it is a little more complicated.
The Analemmatic sundial
The analemmatic sundial is based on an ellipse which is marked out in hour points. The ellipse has major axis of length $M$ aligned $E$-$W$ (so that the $x$-axis is in this direction) and the minor axis of length $m=M\sin(\phi)$ is aligned $N$-$S$. The pointer that casts the shadow is placed along the $y$-axis at a position which depends on the date. This is given by a "{scale of dates}", and some rules for constructing this scale will be given presently.
The pointer casts a shadow which will intersect the ellipse at some point. On the ellipse are marked a series of hour points, and you can tell the time by seeing which hour point the shadow lies on. For an example, look ahead to figure 12 which shows a completed dial, viewed from directly overhead, for Bath, England.
The ellipse
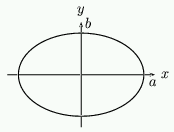
Figure 5: An ellipse.
As ellipses play such an important role in understanding the analemmatic sundial, we include a short discussion on their theory here. An ellipse is an example of a curve called a conic section. Other conic sections are the circle, the parabola and the hyperbola. The Earth travels around the sun on an elliptical path.
If the points on an ellipse have coordinates $(x,y)$ then $x$ and $y$ are related by the formula \setcounter{equation}{1} \begin{equation} \frac{x^2}{a^2}+\frac{y^2}{b^2} = 1 \end{equation} \par If $a=b$ then this is simply a circle. Now if $y=0$ then $x^2=a^2$ so that $x=\pm a$. We will assume that $a>b$ then the $x$-axis is called the major axis of the ellipse and the $y$-axis is the minor axis. \par One particularly nice way to think about an ellipse is to introduce a third variable $\Theta$. Take $x=a\cos(\Theta)$ and $y=b\sin(\Theta)$; then \setcounter{equation}{2} \begin{equation} \frac{x^2}{a^2}+\frac{y^2}{b^2} = \cos^2(\Theta)+\sin^2(\Theta) = 1 \end{equation} so that $x$ and $y$ lie on an ellipse. So if we vary $\Theta$ from $0^o$ to $360^o$ then the points $(a\cos(\Theta),b\sin(\Theta))$ will trace out an ellipse.
Now consider a ruler with points $A$,$B$ and $C$ marked so that the length $AC$ is $a$ and the length $AB$ is $b$. Place this ruler so that $B$ is on the $x$-axis and $C$ is on the $y$-axis. The ruler will make an angle $\Theta$ with the $x$-axis. If the point $A$ has coordinates $(x,y)$, then by construction $x=a\cos(\Theta)$ and $y=b\sin(\Theta)$ so the end point $A$ must automatically trace out the ellipse. This procedure allows us to mark out an ellipse easily and is shown in figure 6.
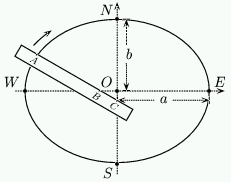
Figure 6: Drawing an ellipse.
There are two points $F_1$ and $F_2$ on the $x$-axis called the {\em foci} of the ellipse located at the points \setcounter{equation}{3} \begin{equation} F_1 = (-\sqrt{a^2-b^2},0) \quad F_2 = (\sqrt{a^2-b^2},0) \end{equation} A remarkable property of the ellipse is that if $A$ is any point on it, the sum of the two distances between $A$ and $F_1$, $F_2$ is constant, so that \setcounter{equation}{4} \begin{equation} \label{eq:ellipse} AF_1 + AF_2 = 2a \end{equation}
| Exercise 2: Using the definition of an ellipse, show that equation 5 is true. |
This gives another method of drawing an ellipse. Take some string of length $2a$ and mark two points, a distance $2\sqrt{a^2-b^2}$ apart, along the line that will become the $x$-axis of the ellipse. Now keep the two ends of the string fixed at these points and place a pencil on the string, pulling it taught. As you move the pencil along it will trace out an ellipse.
How big should I make an analemmatic sundial?
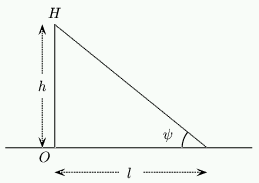
Figure 7: The height of a person.
We will assume that the sundial is to be constructed outside in a garden and the shadow casting object is to be a person who will stand on the dial itself. Have a look at the diagram on the left. The solid line $OH$ represents a vertical object (a person) which we will assume has length $h$. The dotted lines are the rays from the sun.
| {\bf Exercise 3:} Using this diagram and equation 1, show that if the declination of the sun on a given day is $d$ then the length $l$ of the shadow cast by the person at Noon is given by \setcounter{equation}{5} \begin{equation} \label{eq:shadow} l = h \tan (\phi -d) \end{equation} |
Assume we are in Bath, England where $\phi=51.3^o$. At Noon on the equinox, when $d=0$, a person of height $h=1.8$m will cast a shadow of length $l= 1.8 \times \tan (51.3^0) = 2.25$m. On June 21st, midsummer, when $d=23.44^o$, the same person in the same place will case a shadow of length $l= 1.8 \times \tan (51.3^0 - 23.44^o) = 0.95$m. \par You can use similar calculations to ensure an average person, who has height $h$, will cast a shadow on the dial throughout the year by taking the length of a shadow at Noon on midsummer, when $d$ is largest i.e. $23.5^o$ (the shortest shadow throughout the year) as a guide to the size of the minor axis of the ellipse. This is the value that corresponds to $m$ in the following construction.
How is an analemmatic sundial constructed?
There are two stages to building an Analemmatic sundial:
- laying out the hour points, and
- drawing the scale of dates.
Laying out the hour points
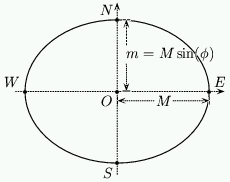
Figure 8: Construction of an analemmatic dial.
-
Find the direction of true North and mark the North--South meridian line on the ground.
-
Mark on an East-West line perpendicular to the North-South line through what is to become the centre of our dial.
-
The major axis of the ellipse will be along the East-West line and the minor axis will be North-South. We will denote the length of major axis (that is the distance from $O$ to $E$ in figure 4) by $M$. For all the calculations here we assume that $M=1$. Such a base ellipse is shown in figure 4.
-
To calculate the value of $m$, the length of the minor axis, we need to know $\phi$, the latitude of the location of the dial. We can then calculate $m$ with the simple formula \setcounter{equation}{6} \begin{equation} m=M\sin( \phi) \end{equation} For example, Bath is $51.3^oN$, so that for $M=1$, $m=0.78$ (to $2$ decimal places).
-
To start the construction of an analemmatic sundial we need to draw an ellipse. As mentioned previously, one way to draw an ellipse is to use string, but in practice the method of using a ruler is much better. Take a ruler or long piece of wood and mark two points $A$ and $C$ on it a distance of $M$ apart. Now mark a further point $B$\ at a distance of $M \sin(\phi)$ from $A$. Your ruler should look like this:
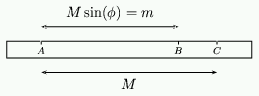
Figure 9: A ruler for drawing the ellipse.
Now draw the ellipse using the ruler as described earlier.
-
When building a sundial it is most common to refer to hours by their {\em angles from Noon}. Twenty four hours make up one day, or rather, one revolution of the Earth. Each hour is then $15^o$ of revolution of the Earth so Noon is $0^o$, $1$ P.M. is $15^o$, $2$ P.M. is $30^o$ and $9$ A.M. is $-45^o$ etc. \par Let $\Theta$ be the angle of the hour. The distance of the point from $O$ along $WE$ is given by \setcounter{equation}{7} \begin{equation} x = M \sin (\Theta) \end{equation} Notice that this depends only on the time and the size of the dial and {\em not} on the latitude. The distance of the point from $O$ along $NS$ is given by \setcounter{equation}{8} \begin{equation} y= m \cos (\Theta) = M \sin (\phi) \cos (\Theta) \end{equation} \setcounter{equation}{9} \begin{equation} x^2 + \frac{y^2}{\sin^2(\phi)} = M^2 \end{equation} This is illustrated in figure 10, and we will explain why in the theory section.
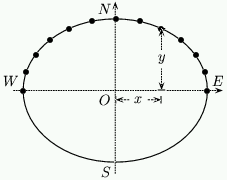
Figure 10: A dial with its hour points.
Note that $\Theta$ is NOT the angle from the noon line to the hour point.
Exercise 4: Show that the angle from the vertical line to the hour point is given by the formula : \begin{displaymath} arctan(\frac{tan(\Theta)}{sin(\phi)}) \end{displaymath} -
To locate the points for hours before $6$ A.M. or after $6$ P.M. you need to know that the dial is symmetrical. Draw a line from an hour point already calculated through $O$ and onto the ellipse on the other side. This is illustrated in figure 11 for $7$ P.M.
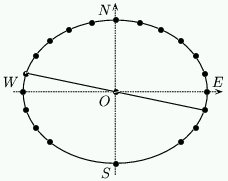
Figure 11: Hour points before 6 A.M. and after 6 P.M.
Example: Bath
For example, the positions of the hour points for a dial in Bath, England are shown in Table 3.
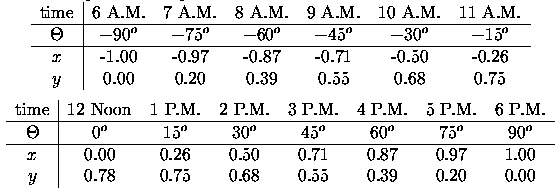
Table 3 - The positions of points for a dial in Bath.
Drawing the scale of dates
The shadow-casting object on an analemmatic dial is movable and its position depends on the date. To see where to place it we must calculate a scale of dates to show the user where to place the vertical pin (or to stand) on any given day of the year. Assuming our dial is in a garden and the person casts the shadow, this will be a scale on the ground on which you stand.
The vertical object (such as a person) is always placed on the line $NS$ a distance $Z$ from $O$. To calculate the distance $Z$ we need to know the declination $d$ of the sun on a given day. Use the values of $d$ given earlier in table 2.
We then use \setcounter{equation}{10} \begin{equation} Z= M \tan (d) \cos (\phi) \end{equation} to calculate $Z$. This formula will be explained in the section on the theory of the analemmatic sundial. For example in Bath we use the following values:
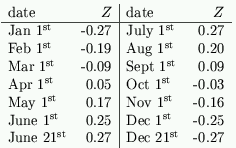
Table 4 - Value Z for an analemmatic dial at 51.3 degrees North.
Figure 12 shows the resulting analemmatic dial for Bath.
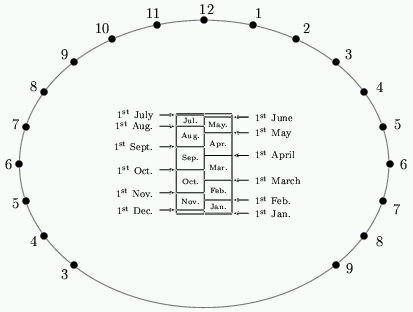
Figure 12: The completed dial for Bath, England.
What kind of time does a sundial show?
Most sundials show what is known as true local time. This differs from the time on your watch, which is called standard mean time. There are two reasons for this.
Firstly, remember that your longitude is the angular distance West of the Greenwich meridian. Round the world there are 24 standard time zones. People living in one time zone all agree to set their watches to the same {\em standard} even though people who are East or West of each other will experience Noon at different times of day. Thus while it is Noon at Greenwich in London, we in Bath have to wait another nine minutes or so because we are $2.3^0$ West. It would be no good if my watch showed 12:00 at Noon because I would have to constantly correct my watch as I moved around. A sundial, which is usually fixed in one place, is designed to read 12 at Noon, and so we need to make the reverse correction. \par Secondly, it may come as a surprise to learn that the days aren't really the same length throughout the year. By this we don't mean it gets darker earlier in winter, but rather that the length of time from one Noon to the next isn't constant. If we divide each day into 24 equal hours, the length of a second will vary from day to day. Your watch is mechanical so that it (hopefully) keeps constant seconds, and these are called {\em mean seconds}. The difference isn't huge but it accumulates over the year so that, for example on 19th February a watch will be 14 minutes fast, and on 27th October it will be 16 minutes slow, relative to the movements of the sun. The graph in figure 13, called the Equation of Time, shows you how to correct for this. To use this figure you take the time measured on the sundial and add the figure for today's date.
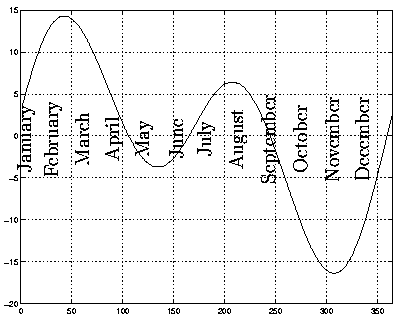
Figure 13: The Equation of Time.
Why does an analemmatic sundial work?
We said earlier that the end of a pointer, pointing at Polaris, casts a shadow that moves round a circle on a disk parallel to the equator of the Earth. To remind yourself of this setup have a quick look back at figure 4. The sun appears to move around the star Polaris in a large circle. At the equinox when $d=0$ this circle is exactly the celestial equator. We can describe the position of the sun by its angle relative to some fixed reference point. For convenience we take this point to be Noon, at which time the sun is highest. The angle $\Theta$ of the sun relative to the Noon point is called the {\em hour angle}, with $\Theta=0^o$ at Noon. In fact $\Theta=15^ox$, where $x$ is the time (in hours) past Noon.
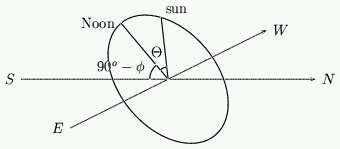
Figure 14: Finding the hour angle.
Now, what shape do we get if we look at the shadow cast by a vertical pointer onto a horizonal surface? To answer this we have to project the circle that the sun makes. If $d=0$ this circle is at an angle of $90^o-\phi$ to the horizontal and intersects the horizontal at $6$am and $6$pm. \par If $R$ is the radius of the circle on which the sun moves and if the $x$-axis is aligned East-West and the $y$-axis aligned North-South, then the $(x,y)$ coordinates of the sun are given by \setcounter{equation}{11} \begin{equation} x=R\sin(\Theta), \quad y=R\cos(\Theta)\sin(\phi) \end{equation} The angle the shadow of the sun makes with respect to the $y$-axis is called the {\em azimuth} and we write this as $z$. It is given by the formula \setcounter{equation}{12} \begin{equation} \label{eq:speri} \cot(z)=\frac{y}{x} = \sin(\phi)\cot(\Theta). \end{equation} During the day, $z$ changes and by finding $z$ we can find the time. For example at $3$pm, $\Theta$ is given by $15^oz\times 3=45^o$ and $\cot(\Theta)=1$. The angle made by the shadow of the sun is then given by \setcounter{equation}{13} \begin{equation} \cot(z)=\sin(\phi) \end{equation}
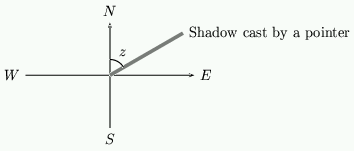
Figure 15: The shadow.
If the declination $d$ is non-zero, the angle $z$ that the shadow makes with the $N$-$S$ line can be calculated using spherical geometry. In this case we modify equation 13 to give \setcounter{equation}{14} \begin{equation} \label{eq:speri2} \cot(z) = \sin(\phi)\cot(\Theta) - \frac{\tan(d)\cos(\phi)}{\sin(\Theta)} \end{equation}
The theory behind this formula is described in the book by Rhor, listed in the Further Reading section. Notice that if $d=0$ then this reduces to equation 13. \par Suppose that we place the pointer at the location $M\tan(d)\cos(\phi)$ on the $N$-$S$ line.
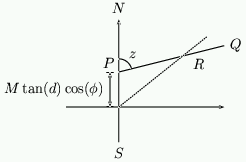
Figure 16: Moving the pointer.
The shadow will be the line $PQ$ starting at the base of the pointer which is at $P$. This line has equation \setcounter{equation}{15} \begin{equation} y= M\tan(d)\cos(\phi) + x\cot(z) \end{equation} \par At the same time, the shadow cast on a day when $d=0$ will go through the origin with angle $z$ given by equation 13. This is indicated by the line meeting the origin in figure 16. \par Using equation 13 this line has equation \setcounter{equation}{16} \begin{equation} y= x \sin(\phi)\cot(\Theta) \end{equation} The two lines intersect at the point $R$ if \setcounter{equation}{17} \begin{equation} x \sin(\phi)\cot(\Theta) = M\tan(d)\cos(\phi) + x \left( \sin(\phi)\cot(\Theta) - \frac{\tan(d)\cos(\phi)}{\sin(\Theta)} \right) \end{equation} Rearranging this expression gives \setcounter{equation}{18} \begin{equation} x=M\sin(\Theta) \end{equation} and therefore as $y=x\sin(\phi)\cot(\Theta)$ we have \setcounter{equation}{19} \begin{equation} y=M\cos(\Theta)\sin(\phi) \end{equation} \par What this shows is that at a given time of the day, the shadow cast by the pointer on the origin on a day with $d=0$, and a pointer at $M\tan(d)\cos(\phi)$ on a day with the sun at declination $d$, {\em always intersect at the point} $R$ which has $(x,y)$ coordinates \setcounter{equation}{20} \begin{equation} \label{eq:analelip} (M\sin(\Theta),M\cos(\Theta)\sin(\phi)) \end{equation} and which lies on the ellipse \setcounter{equation}{21} \begin{equation} x^2 + \frac{y^2}{\sin^2(\phi)} = M^2 \end{equation} \par We conclude that if we draw the ellipse with equation 21 and mark the hour points at the points given by equation 21 with $\Theta=15^o\times$hour past noon, then provided that the pointer is at position $M\tan(d)\cos(\phi)$ then {\em the shadow cast will always intersect the ellipse at the correct hour point}.
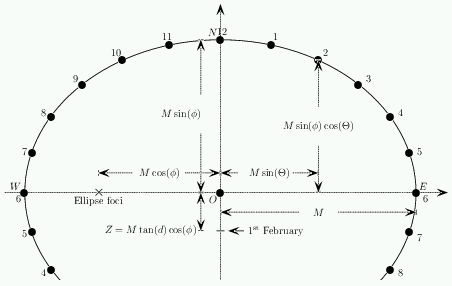
Figure 17: Overall summary.
Further Reading
- Mathematics Galore! by C. J. Budd and C. J. Sangwin. To appear from OUP, 2000.
- Sundials: Their Theory and Construction by A. E. Waugh, Dover 1973.
- Sundials: History, Theory and Practice by R. R. J. Rhor, Dover 1970.
- Sundials & Timedials: A collection of working models to cut-out and glue together by G. Jenkins and M. Bear, Tarquin Publications 1987.
- Sundials on the Internet and the British Sundial Society.
About the authors

Chris Sangwin is a Ph.D. student at the University of Bath, working on dynamical systems and control theory.

Chris Budd is Professor of Applied Mathematics at the University of Bath, and Professor of Mathematics for the Royal Institution. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
Comments
Anonymous
This was an excellent article, providing all the information needed to design a great sundial. I was able to take the equations and construct an excel spreadsheet that constructs a graph chart image for an analemmatic sundial with just the input of the latitude and longitude of the location for which the sundial is to be designed. I added the ability to change the hour locations around the dial slightly to account for the differences between solar noon and standard time noon (I used longitude to do this calculation, so in areas where the time zones are highly erratically drawn, it is not accurate, but works well for most places). The graph chart also plots out the analemmatic gnomon position based on date along the vertical centerline. From all this, I was able print out the graph chart and use spray adhesive to fix it to a sheet of 1/8" copper. I then used punches and a hammer to mark out the sundial. I also etched an equation of time analemma chart onto the copper surface. The result is a beautiful copper analemmatic sundial that is custom designed for my exact location on earth andd from which the true accurate standard time can be read whenever there is sun.
Anonymous
I'd like to construct an analemmatic sundial which gives true clock time for my location. Is this possible? I wondered if it is possible to adjust the position of the points where the gnomon goes to account for the equation of time differences each day?
Anonymous
Yes, but the sun dial will be very full of information -- not anywhere as simple as the sundial depicted and quite difficult to use and enjoy. I live in Houston, Texas. Solar time differs universal coordinated time by anywhere from 4 minutes to 35 minutes throughout the year, with the greatest "spread" between early November and early February when the earth's orbit is moving through the far side of the elliptical (ie: winter). Additionally, you'd have to make adjustments for your longitudinal variance in the time zone.
Anonymous
You are so lucky to be living in Houston, Texas, USA. At the entrance plaza of the Museum of Natural Science is a fountain whose edge has the configuration of the Texas coastline; there is a huge scale model of the Solar System in bronze markers in the pavement (the front step of the Museum is the sun; Pluto is a distant speck next to the street).
But the glory of the plaza is the magnificent Sundial soaring above the fountain, which at Noon focuses a beam of sunlight through a lens on today's date of an analemma marked in bronze on the pavement. This breathtakingly beautiful plaza is a superb marriage of art and science.
Anyone reading this blog: if you visit Houston, don't miss the Museum of Natural Science in Hermann Park. It is enchanting; and if the day is cloudy and you cannot see the great sundial in action, go inside and be fascinated by the elegant Foucault's pendulum; and enjoy the otherworldly beauty of the hall of gems, surely the most serenely peaceful atmosphere of any public space I recall.
Luca Ravioli
This will make a pdf image of the dial similar to what you want. You can print it any size you want. Since the gnomon is printed to it will be sized correctly.
If you make two dials with s curves instead of 8 curves they are much easier to read.
http://www.gcstudio.com/makedial.html
You need to enter your position in latitude and longitude.
If you need to convert the format of your position this page will help:
http://www.gpsvisualizer.com/calculators#airports
Luca Ravioli
If you want the same kind of dial then moving the hours some fraction of the hour to match your location would probably work. As the analemma is in the gnomon position.
This could probably be done mathematically. It is 15 degrees per hour on the earths axis or north star.
Luca Ravioli
That adjustment for clock time involves figures like 4. Also, figures and equations with the Greek letter theta is where the adjustment would be made. 15 [degrees per hour].
Anonymous
how would you feel about sharing your excel sheet? I'm thinking of building one in a garden - London
Thanks
Anonymous
http://web.utanet.at/sondereh/sun.htm
Here is a excellent program!
Charles Hatton
Anonymous
This information is great, I'd love to get a village project off the ground to build one. Just a quick question and I think it may be a stupid one, I assume they do not account for daylight saving.
Anonymous
Thank you for this amazingly informative article. I hardly like to mention that, in equation (4) above, where you have given the equations of the foci of an ellipse, the second set of co-ordinates should refer to F2, and not F3 as listed. I am sure that this is just a typing error and does not detract from the excellence of this treatise.
Sorry for making such a minute correction to this spendid article.
Marianne
Thanks for pointing that out! We've corrected it.
Anonymous
is the ellipse shape applicable within the tropics?
Luis
Does the analemma works or it has to be adjusted to work within tropis?
Dave B
It is, but it overlaps with the gnomon positioning box to the extent your latitude is equatorward of the tropics. At the equator itself the ellipse becomes a straight west-east line
Anonymous
Could you please tell me what t stands for in equation (9)?
I'm stuck ! Thanks.
Marianne
The t was supposed to stand for time, but it should have been denoted by the angle theta. We have corrected it, thanks for pointing it out!
Anonymous
I have seen one of these built at a larger scale in a park. The park's major axis dimension was something like 15 foot. I would like to build one in a garden for children. How can I scale these calculations up to for a larger scale project?
Anonymous
I was wondering how such a sundial works. My father and me are amateur astronomers. We are puzzled and searching for the right description. Thanks for the great article.
Anonymous
Can a sundial (any sundial) work in the tropics, where the sun traverses the sky from north to south during a year?
Anonymous
I think any sundials can work in the tropics because the Sun traverses the sky from from East to West anywhere. Only surface of the sundial must be vertical and top of stick must look at North or South for you can have any shadow on it's surface in any season.
Anonymous
Im confused by the section "Why does an analemmatic sundial work?"
How do I find R radius of the suns motion? What happens if I dont make the ellipse with equation 21 and mark it with equation 22?
How tall should the pointer be? Why is 3pm now given by http://plus.maths.org/MI/26154f8cafc9d116bca498bc09cb0f82/images/img-00…?
Anonymous
Hi guys,
First, thanks for a great article.
As I read it, the idea is that an "average" (180cm) person's shadow hits the ellipse at the right time if they stand on the right date.
Just to confirm, this is different to a "traditional" sundial where it is the edge of the gonome that casts the shadow. In an Analemmatic it is the top of the (vertical) pointer that should intersect with the ellipse?
I ask because I want to use this to make a dial with a fixed pointer (the top will be a literal point), but curved hour lines so that given the date one can tell the time.
m.rik.rutter@gmail.com
Anonymous
Good afternoon, I have constructed a prototype of the sundial for my location. I am facing true North according to my compass, I have placed a figure to represent the mobile gnomon on the correct monthly location. I must be doing some thing wrong because I am not getting the correct time. Is there a crucial step that I have missed?
Anonymous
A compass tells you magnetic north, not true north. You'll have to add or subtract depending on your location from magnetic north (which wanders from year to year).
Here's a site to generate the needed dimensions and positions automatically so you can verify that you've got yours right:
http://analemmatic.sourceforge.net/cgi-bin/sundial.pl
It makes a PDF of plans specific for your latitude and longitude.
Anonymous
I am trying to build one of these and was getting lost in the math.
I really appreciate the theory of it, but was just looking for the plans to place the numbers!
Thank you for posting the sourceforge link.
Have you made a sundial IRL from the PDF it genereates? if so, how accurate is it?
-Tom from New Mexico.
Anonymous
Fascinating. As an ex-RAF navigator, trained in astronavigation, and now retired, and a keen gardener, your article brought together threads from both ends of my life to inspire an interesting and worthwhile project. Now living outside Pittsburgh, Pennsylvania, and quite some way from Bath, I would love to see that Excel spread sheet!
Poo2You
Look - I appreciate ALL the precision and calculations and everything, but sometimes, a GOOD simple sundial DESIGN ought to be considered for those of use who want to keep track of time in the morning sun when reading a book, without having to do MORE calculations just to use it. Come this equinox, I will have a big aluminium plate, tilted to the mid winter angle of the sun above the horizon - or to make it sit on a simple pivot with a wedge or some thing to tilt it for this latitude, and with a short blunt rod poking out of one side... and when the sun moves around, I will mark that spot with a pointy permanent marker and then at the end of the day, I will drill a small hole through it....
I might even scribe and then chisel in a few lines etc...
That is good enough for more than most people.
If people could see them as FUNCTIONAL time pieces rather than astrolabe interstellar calculation engines - anyway I know what I mean....
I am tired, I don't want to do a whole heap of calculations and design work...
I just want to follow the shadow of the tip of the pointer around, with a centre punch and number stamps...
And the equinox dates - that averages out close enough for me.
David Morris
Is it possible to post a picture here? I have built one that has a moving arm which projects a solar disk (spot) onto a drawing on the analemma. When you rotate the arm so that the sun image lands on the proper month marking on the analemma, the time can be read on a pointer pointing at the hours of a clock. I have just built it out of wood, so am testing it, but if it works, it should be accurate to within a minute or two (depending on the accuracy of my wood burned markings and the drawing of the Analemma). Extremely simple to operate. It is called a Heliochronometer. I found the idea in a book called "Sundials", by R. Newton Mayall and Margaret W. Mayall. If it works as advertised, it is simple to build (with one moving part) and simple to use. You can make an adjustment to the clock dial to change it from standard to daylight savings time. Just loosen a screw, rotate the dial one hour, and lock it down again.
Obe Lynd
Do you have a link where we might see a photo of your project? Would you consider posting a follow-up comment letting us know how it turned out for you? And would you be willing to share precise instructions?
robert adzema
I agree with you. Sometimes, a dial that tries to do too much is confusing rather than confirming.