Clustering around the rainbow ray

We want to show that for any point $\alpha _0 \neq \alpha _ m$ the interval $J_2$ coming from any small interval $I_2$ centred on $\alpha _0$ is larger than the interval $J_1$ coming from the interval $I_1$ of the same width as $I_2$ , but centred on $\alpha _ m$ (see the figure).

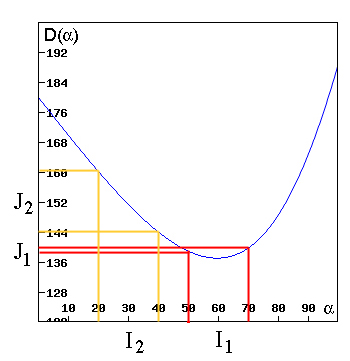
Figure 7: The interval J₁ is smaller than the interval J₂.

Since $\alpha _ m$ is the only point with $D_ f^\prime (\alpha )=0$ we know that $D_ f(\alpha _0)=s \neq 0.$ To match with our figure we’ll assume that $s<0.$ An analogous argument works when $s>0.$

Now choose a positive number $\epsilon$ with $\epsilon < -2s/3$ (you’ll see later why we make this choice). From the definition of a derivative we know that there exists $\delta _1>0$ such that for all $\alpha$ with $|\alpha -\alpha _ m|<\delta _1$ we have

$\begin{equation} -\epsilon <\frac{D_ f(\alpha )-D_ f(\alpha _ m)}{\alpha -\alpha _ m}<\epsilon .\end{equation}$

(1)

Similarly, there exists $\delta _2>0$ such that for all $\alpha$ with $|\alpha -\alpha _0|<\delta _2$ we have

$\begin{equation} s-\epsilon < \frac{D_ f(\alpha )-D_ f(\alpha _0)}{\alpha -\alpha _0}<s+\epsilon .\end{equation}$

(2)

Now choose any $\delta$ less than both $\delta _1$ and $\delta _2$ . Let $I_1$ be the interval $[\alpha _ m-\delta ,\alpha _ m+\delta ]$ and let $I_2$ be the interval $[\alpha _0-\delta ,\alpha _0+\delta ].$

Since $\alpha _ m$ is the only value for which $D^\prime _ f(\alpha )=0$ we know that the maximum of $D_ f$ on $I_1$ must occur at one of the end-points of $I_1$ . Call that point $\alpha ^\prime$ . This means that the width of the interval $J_1$ is $D_ f(\alpha ^\prime )-D_ f(\alpha _ m).$

Since $\alpha _ m$ is the only value for which $D^\prime _ f(\alpha )=0$ we also know that the slope of $D_ f$ is negative throughout the interval $I_2$ . On $I_2$ the function $D_ f$ achieves its maximum at the lower end point $\alpha ^\prime _1$ of $I_2$ and its minimum at the upper end point $\alpha ^\prime _2.$ The width of the interval $J_2$ is therefore $D_ f(\alpha ^\prime _1)-D_ f(\alpha ^\prime _2).$

Now since both $\alpha ^\prime _1$ and $\alpha ^\prime _2$ lie within $\delta _2$ of $\alpha _0$ , we know from inequality 2 that

$(s+\epsilon )(\alpha ^\prime _1-\alpha _0) < D_ f(\alpha ^\prime _1)-D_ f(\alpha _0)$

and

$(s+\epsilon )(\alpha _0-\alpha _2^\prime ) < D_ f(\alpha _0)-D_ f(\alpha ^\prime _2).$

(The inequalities have changed direction because, since $\alpha ^\prime _1<\alpha _0<\alpha ^\prime _2$ , we have multiplied by a negative number in each case.)

Putting this together gives

$\begin{equation} D_ f(\alpha ^\prime _1)-D_ f(\alpha ^\prime _2)=D_ f(\alpha ^\prime _1)-D_ f(\alpha _0)+D_ f(\alpha _0)-D_ f(\alpha ^\prime _2)>(s+\epsilon )(\alpha ^\prime _1-\alpha _0) +(s+\epsilon )(\alpha _0-\alpha ^\prime _2)=-2\delta (s+\epsilon ).\end{equation}$

(3)

Since $\alpha ^\prime$ lies within $\delta _1$ of $\alpha _ m$ , we know from inequality 1 that

$\begin{equation} D_ f(\alpha ^\prime )-D_ f(\alpha _ m)<\epsilon |\alpha ^\prime -\alpha _ m|=\epsilon \delta .\end{equation}$

(4)

And since we have chosen $\epsilon$ so that $\epsilon <-2s/3$ , putting inequalities 3 and 4 together gives

$D_ f(\alpha ^\prime _1)-D_ f(\alpha ^\prime _2)>-2\delta (s+\epsilon )>\epsilon \delta >D_ f(\alpha ^\prime )-D_ f(\alpha _ m).$

Thus, interval $J_2$ is wider than interval $J_1$ . QED.

Back to main article