
The fabulous positional system
The symbols 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, are so commonplace that we rarely appreciate just how special our system of numerals really is. Fifteen hundred years of development have given us an extremely succinct method for writing down even very large numbers. Our numerals have their origin in a system developed by the Hindu scholars of India in the middle of the first millennium AD. Their system was in turn adopted by the Arabs, who ultimately transmitted it to Europe in the twelfth century. For this reason, these numerals tend to be referred to as Hindu-Arabic numerals.
The key to the success of this system is its positional nature. We have a total of ten symbols at our disposal, but we are certainly not limited to writing down ten different values. One of the first things we all learn at school is that our numbers are arranged in columns. Reading from right to left, we first have the units column, then the tens, the hundreds, the thousands and so on. It not only matters which symbols we write down, but also where we place them in this arrangement. This is what we mean by a positional number system. But why should a positional system arise in the first place?
The beginnings of numeration
Map by MapMaster, reproduced under the GNU free documentation license.
The earliest number systems grew out of the human desire to count. The most primitive and basic of all such systems is that of tally marks, in which we place one mark on the page for every item counted. But even if we count up to a moderately sized number, we end up with a sprawling collection of tally marks on the page which are not very easy on the eyes. We therefore introduce extra steps, like letting a diagonal line through four vertical marks stand for five — this amounts to introducing a brand new numeral to our system. We can now write down numbers that are much easier to take in at a glance. But as we write down larger and larger numbers, we find that the notation once again becomes unwieldy. One solution to this problem is to introduce more new symbols. This is precisely how number systems developed historically. As an example of a system with various different symbols, consider the ancient Babylonian system. The first four symbols are give in figure 1:

Figure 1: Babylonian numerals
This system was first developed by the Sumerians around 3500 BC, but it is usually associated with the Babylonians. One hundred is now represented by a single symbol, a vast improvement on our initial tally system. Even large numbers, whose tally form would be horrendous, can now be written down more succinctly. For example, 3,964 is written as follows:
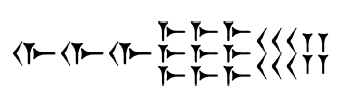
Figure 2: The number 3,964 written in Babylonian numerals.
Notice that even more space is saved by arranging these symbols in columns rather than in a row:

One important thing to notice about these numerals is that the symbol for one always means one, the symbol for a hundred always means a hundred, etc. It doesn't actually matter in which order we write the symbols. The number

also represents the number 3,964; the order of the symbols is irrelevant. The Babylonians tended to use a sensible arrangement: they grouped like symbols together and arranged the groups in ascending order, reading from right to left.
In contrast to the Hindu-Arabic numerals, this Babylonian system is non-positional. Figures 3 and 4 give further examples of non-positional number systems.
Figure 3: Egyptian numerals, ca 3000 BC.
Figure 4: Minoan (Linear B) numerals, ca 1500 BC.
The number systems given in figures 3 and 4 seem a little easier on the eye than the Babylonian system. The reason for this is perhaps the fact that they use only one sign for each of 100 and 1000, unlike the compound Babylonian symbols. Despite this, we continue to concentrate on the Babylonian system, because the Babylonians went on to introduce an innovation which never occurred to the Egyptians or the Minoans (as far as we know...!).
Get into position

Clocks remind us of the Roman non-positional number system and the Babylonian sexagesimal system.
The Babylonians presumably recognised the shortcomings of their non-positional number system. Using the symbols given in Figure 1, they could write down any number up to and including 9,999, but no higher number. If they wanted to write down increasingly large numbers, they would be forced to introduce more and more new symbols. This would have presented them with two problems: increasingly unwieldy notation and the need to remember a large number of symbols. The Babylonians needed a different approach to writing down large numbers. And the new approach was, of course, a positional system.
The first step was to scrap all but the symbols for one and ten. Then, like us, they arranged combinations of these symbols in columns, reading from right to left. However, unlike ours, the Babylonian number system was not decimal, but sexagesimal: successive columns represented the powers of 60, rather than 10. We have inherited this system both for time-keeping and angle-measuring: e.g. 60 seconds in a minute.
In the following example we will draw borders around the columns for clarity, although the Babylonians themselves did not do this. The lowest-value column is the right-most column, which could contain any number up to and including 59 — this is the sexagesimal version of a units column. Any number less than or equal to 59 will appear in this system as it did in the earlier non-positional system, for example 42 is

To go beyond 59, we must add another column to the left, which represents multiples of 60. For example
represents (1 × 60) + (0 × 1) = 60, (the symbol in the right-hand column indicates an empty column — more on this shortly). The string of symbols
represents (11 × 60) + (24 × 1) = 684.
With one column our limit is 59; with two we can write down numbers as high as (59 × 60) + (59 × 1) = 3,599. To go higher, we only need to add further columns to the left, representing multiples of higher powers of 60. If we add a third column, then the value entered there represents a multiple of 3,600 = 60 × 60, and a fourth column would represent multiples of 216,000 = 603. With a three-column arrangement we can write down numbers as high as (59 × 3,600) + (59 × 60) + (59 × 1) = 215,999. In this new scheme our favourite number 3,964 becomes:
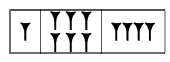
because 3,964 = (1 × 3,600) + (6 × 60) + (4 × 1).
It is easy to see that we can extend this system indefinitely simply by adding more columns on the left. There is no longer a need for new symbols.
A little something should be said about the "-" used to indicate an empty column in the representation of 60. First of all, the Babylonians had no such symbol. They either left an empty space to indicate an empty column, or they did not mark the column at all, creating great potential for ambiguity in their numerals. For example
could denote (21 × 60) + (12 × 1) = 1,272, or (21 × 3,600) + (12 × 1) = 75,612, or (21 × 3,600) + (12 × 60) = 76,320, etc. However, it seems that the Babylonians never had a problem here, since the context always made clear which number was meant. It was not until the Persians inherited the Babylonian number system around 400 BC that a sign was introduced to mark an empty column. The sign was
so 216,001 is written as
The final verdict
Compared to non-positional systems, positional systems are relatively rare in history. However, the benefits of adopting a positional system are clear: they are more concise and easier to use. Our own system takes this conciseness to extremes: rather than having a combination of digits making up the value in each position, we have precisely one symbol per position. It is easy to see why the Babylonians didn't adopt this way of doing things themselves: they would need 60 symbols in total, so their system would be rather hard on the memory. Our "single symbol per position" means that our numerals are as concise as they can possibly be. Just compare our way of writing 9,876,543,210 with the Babylonian counterpart

The Hindu-Arabic numerals have their own downside however. All our numerals 1, 2, 3, 4, 5, 6, 7, 8, 9, are abstract symbols that have little or no connection with the quantities they represent, other than the connection we impose upon them. The Babylonian way of writing "two" is more visibly connected with the quantity two than the symbol 2. In order to do arithmetic in our numerals, we must be familiar with their rules of operation. We must know that when we add the symbol 1 to the symbol 2, we get the symbol 3, and so on. We need to know our times tables. We need to know that when we add 1 to 9 in a particular column, then we must enter 0 in that column and add 1 to the next column to the left. When listed like this, these rules begin to sound complicated, which indeed they would be to an external observer who has no prior knowledge of our numeral system. We all have a certain facility with these numerals because it is drummed into us from an early age. Arithmetic in Babylonian numerals, on the other hand, is much more mechanical. We can still take the "column-by-column" approach, but we now need only to gather together like symbols and then apply the following two rules:
| 1) Replace every ten occurrences of | by one | . |
| 2) If six of | occur in a particular column, then delete these and | |
| enter a | into the next column on the left. |

Hindu-Arabic numerals: much loved and indispensable.
After singing the praises of fabulous positional systems, I do not want to diminish the value of our own numerals in any way. The fact is that we find them easy to use — whether this is because we are instructed in their use from an early age, or because they are inherently easy to use is immaterial, at least from a pragmatic point of view. In truth, these numerals are so ubiquitous (more so than the Babylonian numerals ever were) that we would find it extremely difficult to change them, even if we wanted to. It looks like they're here to stay! So next time you're checking your bank balance or dialling a phone number, spare a thought for the centuries of development that have gone into producing these invaluable signs.
About the author

Christopher Hollings did his degree and PhD in mathematics at the University of York. He is now a post-doctoral researcher at the Centre of Algebra at the University of Lisbon. His main areas of interest are semigroup theory and the history of mathematics. He loves to write, both for professional reasons and for recreation. Other hobbies include reading and photography, as well as trying very hard to speak Portuguese.
Comments
Charles John
Really inspired to have stopped by your article. I was in a constant search for the origin of number system for the past two weeks and this article helped in connecting the dots. Learning the history of any subject brings clarity, thank you for posting this article Chris.
However I'm would still like to know more, about the column wise segregation developed by Babylonians. You've clearly mentioned "The how", But i believe this technique was not developed out of the bloom. Is there any archeological findings or a detailed history that you missed out to explain. Coz, i feel a sudden jump in the story of the progress of the system.
Babylonians developed symbol for every numbers, till 60. But then, they dramatically created this positional system. Sorry but i feel a gap here.
Bertram Vermont
Hello Chris Hollings,
I've been interested in the origin of the positional number systems ever since I worked repairing computer hardware starting in the 1970's. I would enter a 15-bit binary number (using octal coded binary to remember easier) into several memory locations using a bank of switches. With this small program the computer loaded in a punched paper tape with a much larger program. Thus, I learned 2 positional number systems. Your explanation of the history was done very nicely. You made it easy to understand. Thanks for your excellent article.