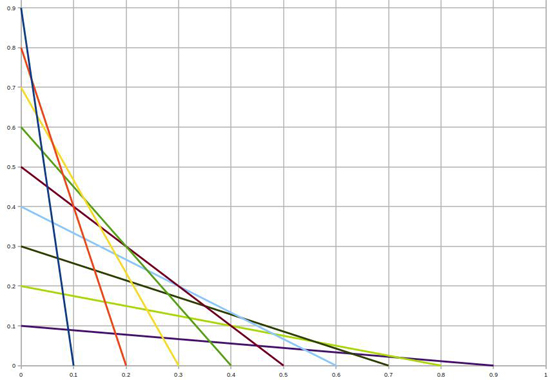
We want to find the formula for the intersection between any two adjacent lines in our bridge.

Let's look at a line that intersects the $x$ axis at a certain point $t.$ Its function, $y_t(x),$ is 0 at $t,$ and $1-t$ at 0. $$y_t(t)=0$$ $$y_t(0)=1-t.$$ The general equation for such a line is $$y_t(x)=(1-t)-x\frac{1-t}{t}.$$ Now let's look at a line which intersects the $x$ axis at some point $t$ and the line just after it, which intersects the $x$ axis at a point we call $t+\Delta t.$ The curve we are after is the one we'd get if there were infinitely many chords. In other words, as the spacing of our chords on the $x$ axis, $\Delta t,$ approaches 0, the point in which our two lines intersect approaches a point on our envelope. Let's first find the intersection point of our two lines by setting $$y_t(x)=y_{t+\Delta t}(x).$$ This gives \begin{eqnarray*} (1-t)-x\frac{1-t}{t} &=& (1-t-\Delta t)-x\frac{1-t-\Delta t}{t+\Delta t} \\ -x\frac{1-t}{t} &=& -\Delta t -x\frac{1-t-\Delta t}{t+\Delta t} \\ -x(1-t)(t+\Delta t)&=& -x \cdot t(1-t-\Delta t)-\Delta t \cdot t(t+\Delta t) \\ x &=& t^2 + t\cdot \Delta t \end{eqnarray*} As $\Delta t \rightarrow 0$ we get $$x=t^2.$$ Putting this in $y_t(x)$ we get \begin{eqnarray*} y_t(t^2) &=& (1-t)-t^2\frac{(1-t)}{t} \\ y_t(t^2) &=& (1-t)^2.\end{eqnarray*} So we now know that our curve is defined as all the points that satisfy $$(x,y) = (t^2, (1-t)^2)$$ for all $t$ in [0,1]. So the curve we are after is $$y(x) = (1-\sqrt{x})^2.$$

Back to main article.