
Walk, trot, gallop

A dressage horse and rider performing the extended trot. Image: Chefsna.
The abilities of equestrian athletes are amazing, but the skills of their horses are even more impressive. Through training, the horses can perform complicated movements with speed, elegance, and precision. But the training builds on innate features of horses, which are remarkably versatile, even in the wild. In Charles Dickens's Nicholas Nickleby, Wackford Squeers, the disreputable teacher who runs Dotheboys Hall, shows off his erudition: "A horse is a quadruped, and quadruped's Latin for beast, as everybody that's gone through grammar knows." Squeers is wrong about the Latin, but right about horses being quadrupeds: animals with four feet. With four feet, you can make a lot of movements that are impossible with two.
Horses move using several different patterns, and those patterns have striking mathematical features. At slow speeds, horses walk. Here the legs hit the ground at regular intervals in the order back left, front left, back right, front right. To move faster, they trot. Now diagonally opposite pairs of legs move together, so that the left back and right front legs hit the ground at the same time, and then the other two legs hit the ground together. For really rapid movement, the horse gallops. Here the timing is more complicated. The two back legs hit the ground almost together, but one of them (say the right) is a split second behind the other one. Then the same thing happens with the front two legs, and again the left one hits the ground first. Many horses can also canter, an even more complicated pattern used at speeds between trot and gallop. Sometimes this comes naturally, sometimes it is the result of training. Other horses can pace: now the two left legs move together, then the two right ones.
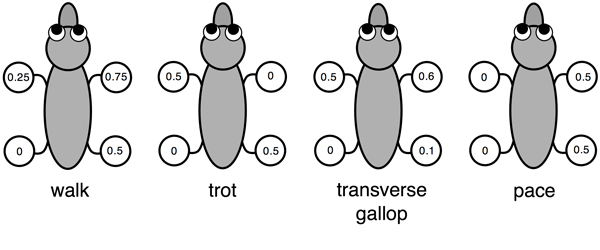
Four different gaits: the numbers in the feet of this creature show when the particular foot hits the ground, as a fraction of a complete cycle.
The branch of science that studies animal movements is called gait analysis. A gait is a pattern of leg movements, and five of them have just been described: walk, trot, gallop, canter, pace. Strictly speaking, the gallop of the horse is a transverse gallop. There is another kind, the rotary gallop, in which the legs at the front hit the ground in the opposite order to those at the back. This is how cheetahs move when they are chasing prey. Gait analysis applies to all animals with legs, including insects, with six; spiders, with eight; and humans, with two. It seeks to understand the general principles of legged locomotion in nature. Those principles also apply to creatures that use wings, or fins, or wriggle—like snakes. Even snails have their own characteristic gaits.
Mathematics is used in gait analysis in several different ways. At the simplest level, it describes the patterns. This description provides clues about the networks of nerve cells that control the gaits, known as central pattern generators. In many animals it is virtually impossible to observe these networks directly, but the timing patterns provide clues that suggest what symmetries the central pattern generator should have.
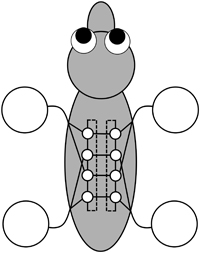
Analysing the symmetries of the walk shows that the central pattern generator should have the same symmetries as two loops of four identical components, linked left-to-right.
For example in the walk, each leg hits the ground one quarter of the gait cycle after the previous leg, so the central pattern generator must have a symmetry that naturally leads to these quarter period phase shifts. There is also a left-right symmetry. Putting all of the information together, and making some reasonable assumptions, it turns out that the central pattern generator should have the same symmetries as two loops of four identical components, linked left-to-right. It need not have this form in a literal sense, because other arrangements can have the same symmetries, but even so, we can make some predictions about the motion that have been verified experimentally.
The mechanics of the movement is also important—how the forces exerted by the muscles act on the bones and joints of the horse's skeleton. In simple models the horse is treated like a table whose legs are hinged, so that they can move, and are supported by springs. Better models correspond more closely to the actual arrangement of muscles and bones.
So why do horses use different gaits at different speeds? It's a bit like the gears on a car. Patterns of movement that work fine at slow speeds become inefficient, or mechanically unworkable, at higher ones. To convince yourself of this, try walking faster and faster. At some point you will find that however hard you try, you don't speed up. But if you switch to a run, a different gait, going faster is suddenly easy. Experiments have revealed a close connection between a horse's gait, speed, and oxygen consumption. At low speeds, the walk uses least oxygen. At higher speeds, the trot takes over. At higher speeds still, the gallop makes the best use of the available oxygen. However, the walk can be sustained for much longer than the trot, and the trot can be sustained for longer than the gallop—just as we can walk for longer periods than we can run. Mathematical models help to explain these observations.
Gait analysis has important applications to medicine (disorders that affect movement, especially in young children), robotics (robots with legs can move in difficult terrain), and sport. Which brings us back to the Olympics. When you watch the equestrian events, keep an eye out for regular patterns in how the horses are moving. For that matter, do the same for the human athletes. The same mathematical principles govern how a horse jumps a gate, and how a human runs a hundred-metre sprint.
Further reading
- You can read more about central pattern generators in the Plus articles Chaos in the brain and Controlling cockroach chaos;
- And about modelling gaits in the Plus article Modelling, step by step;
- And about the mechanics of movement and medical engineering in the Plus article Shaping our bones.
About the author

Ian Stewart is Professor of Mathematics at the University of Warwick, popular mathematics and science fiction writer and recipient of the Christopher Zeeman Medal. Some of his books have been reviewed on Plus: