Chomp - Square and Thin

Square Chomp

How can the first player (Player A) of a game of Square Chomp guarantee to win? Simple. The first move is to chomp all the cookies except those along the left and bottom edges.

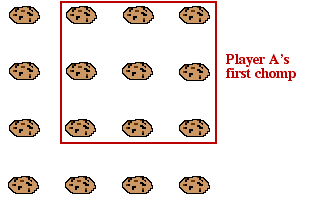
If the second player (Player B) now chomps the poisoned cookie, she has lost, so we can assume she doesn't. So she must chomp either some cookies along the left edge, starting from the top, or some cookies along the bottom edge, starting from the right side.

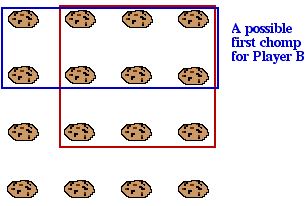
Player A should then chomp the "symmetric cookies" - the matching cookies along the bottom edge if Player B chomped some on the left edge, and vice versa.

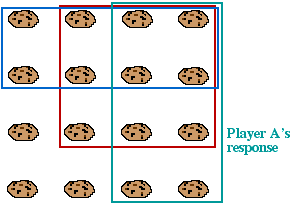
At each stage, either Player B will chomp the poisoned cookie, or she can only take cookies from the left edge or bottom edge, but not both. So at each stage Player A can reply by taking the "symmetric cookies", until only the poisoned cookie is left, which Player B has to eat.

Thin Chomp

The analysis of Thin Chomp is a little more complicated, but not much. Clearly Player A can win Chomp played on the shortest possible "Thin Grid" - a grid of just 2 cookies. We will use a recursive argument - showing that if Player A can win Chomp played on all Thin Grids 1,..,n-1 cookies long, then she can win on a Grid n cookies long.

On a Thin Grid n cookies long, Player A should start by taking just the top righthand cookie.

If Player B now chomps any cookie from the bottom row, she has transformed the game into Chomp played on a shorter Thin Grid, and Player A can win. So we can assume she doesn't take any cookies from the bottom row.

If she chomps all the cookies from the top row, then Player A can chomp all the cookies left except the poisoned one, and again Player B loses.

So we can assume that Player B chomps some but not all of the cookies in the top row. This means there are at least two more cookies left in the bottom row than in the top row.

Player A should now chomp only cookies from the bottom row, leaving exactly one more cookie in the bottom row than are left in the top.

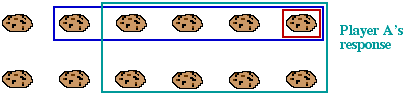
Then Player B's move can be analysed in exactly the same way as for her first move, and we come to the conclusion that if she is not to lose, she will have to chomp some but not all of the cookies in the top row. But there are only finitely many cookies in the top row, so eventually this won't be possible, and Player B will lose.

Back to main Mystery Mix page