
They never saw it coming
Motion camouflaging and nature's stealth fighters
The word "stealth" is often associated with high-tech bombers built to be invisible to enemy radar. This technology works through the aircraft's surface being specially designed and having a covering of radar-absorbent skin that ensures minimal radio waves are reflected back to the enemy radar transmitter.
There is another kind of stealth, however, that does not rely on hiding the presence of an object, but on masking the fact that it is moving. If the pursuer approaches along a particular trajectory it appears to remain perfectly stationary from the point of view of the target. The pursuer can use this "motion camouflage" to rush right up to the target before it is perceived as a threat. This technique could be used by missiles to remain undetected for as long as possible, and even appears to have been discovered by nature. There is good evidence that hoverflies and dragonflies have evolved this strategy to fly without being detected.
Visual motion
Whenever you move, the visual scene viewed by your eyes changes in a predictable way. For example, when you look out of a train window, close-by objects (like trees lining the track) really seem to race past, but far-off things (such as hills in the distance) hardly seem to move at all. The angle between you and a stationary object changes smoothly, but for near objects this angle changes more rapidly than those far away. Very distant objects are effectively positioned at infinity and do not seem to shift at all - the angle remains constant.
The trick behind motion camouflage, then, is essentially to move in such a way that the angle between yourself and your target changes at a specific rate to mimic the motion of an object at a specific distance. If you move so that this angle remains constant, then from the point of view of the target you will appear stationary at a fixed distance away - an innocent speck on the horizon that poses no threat. For example, if your friend is running through a field you can motion camouflage yourself from him by walking in a curve that ensures you are always between a tree and him - you will appear to be stationary at the base of the tree.
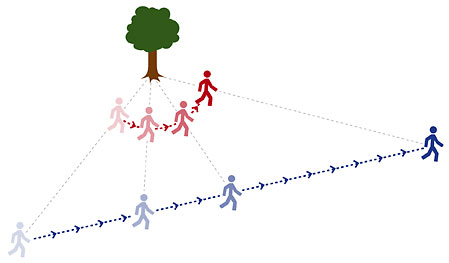
Although you (the red person) are moving, you will appear stationary to your friend (the blue person).
You can go one better, though, and chase after your friend without him even realising you've moved from the foot of the tree. As long as you're always positioned on the "constraint line" joining the target and your chosen fixed point you can move towards him and still appear to be absolutely stationary. As long as your friend doesn't notice that your apparent size is increasing as you approach, or that your legs are moving, you might be able to get quite close before you're spotted. Of course, if your friend is stood still the whole situation simplifies, and you only need to walk in a straight line towards him. But if you want to pursue a moving target the stealth path becomes a graceful curve, the properties of which we will now explore as a good example of the mathematics of vectors.
Vector geometries
Let's consider the trajectory of motion camouflage in a plane - i.e. with only two dimensions to worry about. The position of the target can be given with two co-ordinates, (x,y), or more usefully here as a position vector, $$\left(\begin{array}{c} x \\ y \end{array}\right)$$ (vectors are signified by bold face). This position changes as the target moves, and so the position vector is a function of time, a(t). The position vector of the chaser is b(t). The position vector of the stationary point is not a function of time, and is called b0. As can be seen in the diagram below, the vector of the line joining the target and the stationary point - the "constraint line" - is simply a(t) - b0.
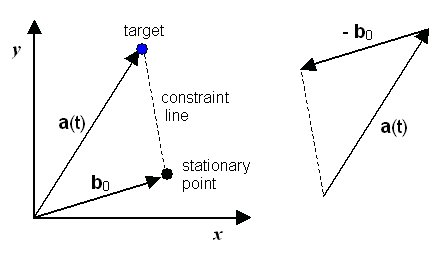
The geometry of the constraint line
If the pursuer is to motion camouflage itself, then, it must make sure that it remains somewhere on the constraint line joining the target and the stationary point. The simplest condition is if the pursuer uses its starting position, b(0) (i.e. when t=0), as the stationary point it mimics. Thus b0 = b(0). A typical motion-camouflaged pursuit can be seen in the diagram below.
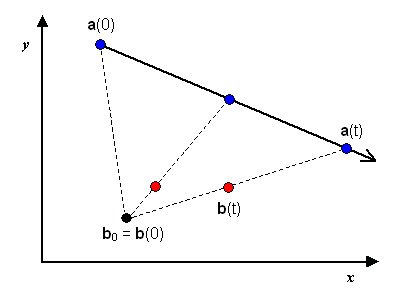
The pursuer (red dot) is moving along the constraint line towards the target (blue dot)
For the pursuer to remain disguised, its position at all times must satisfy this equation:
b(t) = b0 + f(t)(a(t) - b0). (Equation 1)
f(t) is a function that must give values between 0 and 1, as it defines how far along the constraint line (a(t) - b0) the pursuer has advanced. Thus in English this equation simply means: "The position of the pursuer at any time must equal the stationary point plus some proportion of the constraint line".
When f(t) = 1 ...
b(t) = b0 + f(t)(a(t) - b0);
b(t) = b0 + (a(t) - b0);
b(t) = a(t).
... the pursuer has exactly the same position as the target and so finally captures it. The time value T for which f(T)=1 is called the capture time - the length of time it takes the pursuer to catch up with the target. Of course, if the pursuer moves slower than the target it may never catch up and no value of T exists. A slow pursuer with a target moving towards it, though, may be able to use motion camouflage to set up an ambush.
It is the function f(t) that describes the way the pursuer approaches along the constraint line and so the form of the motion camouflage trajectory. Any function that has a range 0 ≤ f(t) ≤ 1 will produce a motion camouflaged path along the constraint line. But if both target and pursuer are moving at a constant speed there exists an unique solution of f(t). $$|{\bf \dot{a}}(t)| = |{\bf \dot{b}}(t)| = 1,$$ (that is, the size of the rate of change of target position with respect to time, i.e. its speed, equals that of the pursuer, and both are constant).
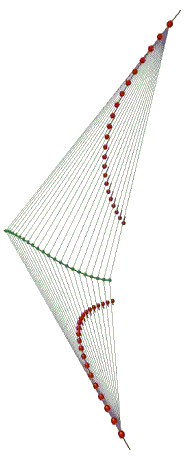
Two motion camouflaging hunters (red dots) converging on the same prey (middle green dots). Image courtesy of Dr. A. Anderson.
When Equation 1 is differentiated with respect to time and then rearranged, the rate of change of f(t) (written f'(t) or df(t)/dt) is given in terms of a quadratic equation. One solution is the normal disguised approach, but the other (with the negative term) describes a stealthy defence - retreating along the constraint line to avoid the target. As we will see later, the attack approach is found in nature, but no animal has yet been discovered that uses motion camouflage as an escape technique.
More complex scenarios, such as target or pursuer moving at a non-constant speed, cannot be solved exactly. They can be numerically modelled on a computer, however, and the positions and flight vectors of the two individuals calculated at every time-step. The trajectories can then be plotted to display the graceful tracks as the pursuer homes in on the target, such as in the diagram to the right.
The f(t) function is itself very interesting. Depending on the desired strategy, the pursuer can solve the motion camouflage equation in many different ways. There are infinitely many ways of moving along the constraint line, but only one solution is optimal in terms of minimising the total distance travelled, or the time until interception (t), or that limits the maximum speed required to remain camouflaged.
Motion camouflaging in nature?

Certain flying insects are thought to employ this motion camouflaging. The male hoverfly sometimes shadows a female in flight. Once he spots one he tracks her in what seems to be a motion camouflaging trajectory, but keeping a roughly constant distance away (maybe so as not to alert her by his increasing apparent size, as mentioned above). As soon as she lands (and is unable to escape quickly) he rapidly darts in to attempt to mate. Biologists have also collected evidence that male dragonflies attempt to use motion camouflage against each other when they are "dog-fighting" over territorial claims.
It has even been demonstrated that humans are susceptible to the trickery of motion camouflaging. People were tested using a computer game that simulated a spaceship flying down a tunnel with missiles being fired at it. They turned out to be much slower to spot and shoot down motion camouflaged missiles than those employing the traditional pursuit trajectory of "travel at constant speed directly towards the target".
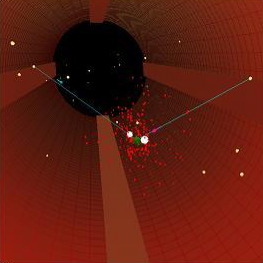
A screen shot of the computer program written to test the susceptibility of humans to motion camouflaging trackers. Image courtesy of Dr. A. Anderson.
Motion camouflaging has been an exciting field of research since its discovery (by humans, anyway) 10 years ago. Since then there have been experiments suggesting that several insect species have evolved this ingenious method of creeping up on an unsuspecting target, and research showing that we ourselves find it hard to detect motion camouflaged objects. There is a lot of interest in these techniques from the military, and also from the computer games industry. So don't be surprised if you start finding yourself up against motion camouflaged missiles in Level 5 in a few years...
If you do suspect that your computer-generated enemy is targeting you with motion camouflaged missiles, the best defence strategy to break the camouflage would be to fly fast and erratically. Any pursuing missiles might find that they cannot accelerate hard enough to maintain themselves on the rapidly shifting constraint line, and would be forced to suddenly begin mimicking a different stationary point. From your point of view, what you thought were stationary points on the horizon would now appear to quickly jump between different locations - a sure sign that they were artificial and trying to shadow you without being detected.
Further Reading
Dr Andrew Anderson performed the original research into human susceptibility to motion camouflaging, and has also studied the algorithms that simple insect brains might use in order to fly the exact trajectories necessary. He has a good website on many aspects of motion camouflaging, with links to his published research papers.About this article

Lewis Dartnell read Biological Sciences at Queen's College, Oxford. He is in his second year of a four-year combined MRes-PhD program in Modelling Biological Complexity at University College London's Centre for multidisciplinary science, CoMPLEX. In 2003 he came second in the THES/OUP science writing competition, and in 2004 he came second in the Daily Telegraph/BASF Young Science Writer Awards. You can read more of Lewis's work at www.ucl.ac.uk/~ucbplrd.