
Lagrange and the Interplanetary Superhighway
Analysis and the winning of a prize

Nicolaus Copernicus, 1473 - 1543.
Around the turn of the 15th century, Copernicus came up with the revolutionary idea that the planets orbit around the Sun. Although this new view of the world was received with hostility in some quarters, notable scientists, including Kepler and Galileo about a century later, came to accept it. But how exactly did the planets move? Did they describe circles, as Copernicus thought, or ellipses, as observation seemed to suggest?
It took 150 years and the brilliant mind of Isaac Newton to come up with a mathematically rigorous answer. He considered a simplified problem in which just two massive bodies orbit around each other, each exerting a gravitational pull on the other. Using his new technique of calculus, Newton took his equation describing the force of gravitational attraction and integrated it. His solution showed that the path of a planet is always an ellipse.
In fact, what Newton considered was the way in which an object falls through a gravitational field, and he found that, along with the ellipse (or the special case of a circle), there are another two possible paths for a falling object. These are the well-known parabola of a cannonball, and the hyperbola of an object with enough velocity to completely escape the gravitational pull - such as the Voyager 2 probe now leaving the solar system at nearly 45,000 mph. These three trajectories are known as conic sections, as they are also the curves produced by cutting a cone along different planes.
Newton had shown that the "two body problem" was integrable, and so could be solved exactly. His magic formula can tell you precisely where the Earth is in its orbit around the Sun for all time, no matter how far in the past or future - as long as you assume that the Earth and the Sun are the only celestial bodies. After this triumph of cutting-edge mathematics (back in the seventeenth century) the next natural step was to ask about the "three body problem" - could another precise "analytical" solution be found for a solar system composed of the Sun, Earth and Jupiter, for example? This question is much more difficult, as the changing gravitational tug of all three bodies produces very complex behaviour. In fact, without quite realising it, mathematicians at the time had stumbled across one of the first examples of chaos. They soon realised that the three body problem is not integrable, which means that no exact solution can ever be found.

Isaac Newton, 1643 - 1727.
If certain simplifications are made, however, the problem can once again be solved analytically. The "restricted three body problem" assumes that one of the three masses is negligible, and so exerts no gravitational influence on the other two. The problem is now like tracking the path of a mote of dust as it falls through the gravity field of the Earth and Moon.
Two great mathematicians, Euler and Lagrange, shared a prize offered by the Paris Academy of Sciences in 1772 for their solutions to this problem. Their analytical solution showed that there exist special regions in the space surrounding two bodies like the Earth-Moon system within which a particle, or spaceship, can orbit naturally while maintaining the same position with respect to the other two.
Euler found three such locations, but Lagrange's analysis was more thorough and he discovered an additional two less obvious points. Not that Euler should feel cheated however, as he had already lost sight in both eyes and completed the entire solution in his head! But neither of them could have had any idea how important their work would become 200 years in the distant future, with our spacecraft now routinely voyaging through the inky blackness of the solar system.
Lagrange points
These unique regions in space became known as Lagrange points, and there are a total of five in every two body system. To understand the mechanics of these five points, let's take as an example the system arising from the Earth, the Moon and a spaceship. To keep things simple, let's assume that the Moon and the spaceship both orbit the Earth in perfect circles, and that the spaceship exerts no gravitational pull on the other two.

Leonhard Euler, 1707-1783.

Joseph-Louis Lagrange, 1736 - 1813.
$$F_c = m v^2 / r, $$ where $m$ is the mass of the object, $v$ is its velocity and $r$ the distance from the centre of the circle. In our example, this centripetal force is supplied by the Earth's gravitational pull, which according to Newton's law of gravitation is $$F_g = GMm/r^2 $$ where $M$ is the mass of the Earth, $G$ the gravitational constant, and $m$ and $r$ are, as before, the mass of the object and its distance to the centre of the Earth. If an object of mass $m$ orbits the Earth at distance $r$ then the gravitational pull of the Earth must supply exactly the centripetal force needed to keep it in orbit, so $$GMm/r^2 = m v^2/r .$$ Rearranging, this gives $$v = \sqrt{GM/r}.$$ So for the object to be orbiting Earth at distance $r$, its velocity must be exactly $$v = \sqrt{GM/r}.$$ Any slower and the Earth's pull will make it spiral in until it reaches its natural orbit, any faster and it will migrate outwards a short way.
This formula also tells us that the further an orbiting object is from the Earth, the longer it will take to complete one full turn around the Earth: $v$ decreases as $r$ increases. A spaceship orbiting Earth further out than the Moon will take more time for a complete turn than the Moon, while one further in will take less.
But so far we have ignored the influence of the Moon's gravity on the spaceship. Suppose, for example, that the spaceship sits on the straight line segment connecting Earth and Moon. Then the gravitational pull of the Moon will counteract that of the Earth. The net force the spaceship feels is reduced; the centripetal force is weakened. This means that the spaceship orbits slower than it would if the Moon wasn't there. In fact, there is one point on the line between Earth and Moon where the spaceship orbits Earth at exactly the same speed as the Moon, and this in one of the Lagrange points.
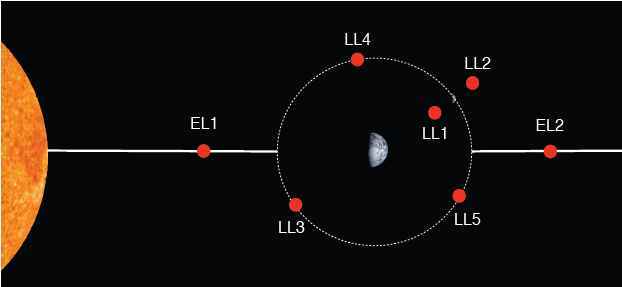
Figure 1 - not drawn to scale.
There are four other points at which the combined gravitational pull of Earth and Moon exactly balances the centripetal force. As the solar system turns, a spaceship sitting at these points always maintains the same position with respect to Earth and Moon.
The diagram in figure 1 shows the Lagrange points in Earth's neighbourhood - made up of all five due to the Moon, and two of those from the Sun. The first three Lunar Lagrange points (LL1, LL2 and LL3) all lie on the line joining the Earth and the Moon and were the ones found by Euler. LL4 and LL5 each form the third point of an equilateral triangle and so always keep 60° in front and behind of the Moon as it circles the Earth.
These Lagrange points are not merely mathematical curiosities, though, as they are already being used by spacecraft exploring the solar system. Of course our model above is very simplified: there are more than just two massive bodies in the solar system, the planets' orbits are elliptical rather than circular, and there are other forces at work, not just gravity. Nevertheless, calculations along similar lines as the ones above still approximate reality well enough to be used in real-life space travel.
At any of the five Lagrange points, a spaceship can maintain a fixed position with respect to the two larger bodies with relatively little effort, and so they are perfect for long-duration space missions. The EL1 point is currently orbited by the Solar and Heliospheric Observatory Satellite (SOHO) as it offers an unrestricted view of the Sun, and WMAP is observing the left-over radiation of the Big Bang from its orbit around EL2.
Different kinds of equilibrium
The exact dynamics around some of the Lagrange points, however, is far more complicated than Euler and Lagrange could have predicted. Understanding it requires the full power of modern dynamical systems theory. The two points L4 and L5 are "stable equilibria". In other words, if a spacecraft placed at this location becomes nudged, or perturbed, it will naturally return to its original point. It is like a marble placed in a wash basin. The slightest displacement away from the bottom moves the marble up the curved side. It might roll round in circles for a bit, but it will always eventually return to the plug hole. Similarly, a spacecraft can stably orbit around the empty space at L4 or L5.
The first three Lagrange points L1, L2 and L3, however, are "unstable equilibria". They are examples of "saddle points". Instead of a wash basin, think of a horse-riding saddle. It curves upward in one direction but downward along another axis. This means that if the marble is nudged even minutely away from the equilibrium point, it starts falling down the gradient and will never return. Similarly, a spaceship at L1, L2 and L3 will drift off at the slightest disturbance. SOHO and WMAP both need to fire their thrusters about once a fortnight to keep themselves orbiting their unstable Lagrange point.

Figure 2 - not drawn to scale. Image courtesy of NASA.
Figure 2 shows a map of the gravity field of the Sun-Earth restricted three body problem. The contours show that the steepest gradients surround the Earth and Sun, with the five Earth Lagrange Points located in equilibrium regions with relatively gentle gradient. L1-L3 are unstable saddle points, and spacecraft positioned here will always drift away from the equilibrium. L4 and L5 are stable equilibria, and objects can orbit here indefinitely. The blue arrows show that L4 and L5 are actually atop a potential hill - it is the additional effect of the "Coriolis force" that makes them stable.
So some of the most advanced machines ever built are using special equilibria points that were found two centuries ago, along with some more recent mathematics in the form of stability analysis and dynamical theory. But the importance of the unstable Lagrange points does not stop here. As we've seen, analysis with calculus can find exact solutions to the equations describing only two massive bodies. How can we ever predict anything about the motions of all nine planets within our solar system?
Until recently mathematicians simply ignored the interactions between the planets' gravitational forces, an assumption that works fine to a certain level of accuracy. But now with the advent of ever faster supercomputers, mathematicians can use a much more brute-force approach and calculate numerical solutions. Instead of attempting to solve the equations exactly, they model a complex system step-by-step, crunching through an enormous number of separate integration calculations to see how the system behaves over time. With this technique, something very surprising has been discovered about the dynamics of our own solar system, and it all comes back to the old Lagrange points. But first, we need to learn a little bit about space travel.
Ultra-low energy trajectories
Moving between different positions within the gravity field of the solar system requires energy. The space shuttle must obviously expend an enormous amount of fuel to launch itself against the pull of gravity into an orbit 400 km over the Earth's surface. The Apollo spacecraft had to fire rockets to lift their astronauts even further up to get to the Moon, and then again to bring them home afterwards. Even though there is no air friction, moving between two positions in the solar system usually requires a rocket burst to provide a change in velocity, or "delta V" as it is known. The delta V needed to reach a low Earth orbit (LEO) from the ground is 9.7 km/s (about 22,000 mph). The delta V to lift a spacecraft from LEO to the Lunar Lagrange point LL1 is a further 3.15 km/s (much less because the strength of gravity decreases with distance).Now, it just so happens that the delta V needed for the one and a half million kilometre journey from LL1 to EL2 is only 0.014 km/s - no faster than a cyclist! The fact that the energy levels of this Lunar Lagrange and Earth Lagrange point are so similar is purely a coincidence, but it opens up a fabulous opportunity for space exploration. There is an ultra-low energy pathway between these two crucial points in space - meaning no "uphill struggle" in either direction and spacecraft can travel between the two with virtually no fuel.
More and more satellites are being planned for the Earth Lagrange points. If any of them were to break down so far from home they would be virtually impossible to retrieve or repair. Sending astronauts up to fix the Hubble Space Telescope in Earth orbit was difficult enough. Getting astronaut mechanics out to EL2 would require not only a rocket as big as that which took men to the Moon but a voyage time of three months one-way, all the while exposed to the harsh space radiation outside Earth's magnetic field.

No faster than a cyclist
However, due to this low-energy pathway, faulty spacecraft could be commanded to coast back to LL1, practically for free. NASA has been seriously considering LL1 as an ideal location for a permanent space-station. Not only would a space habitat be an astounding human achievement, but it could serve as a repair station for faulty satellites returning along the EL2-LL1 pathway.
An interplanetary superhighway
But how do these low energy pathways arise? Can we find more of them and so enable our spacecraft to tour the solar system virtually for free? The foundations for the discovery of such a network was laid in the late 19th century by the legendary mathematician Jules-Henri Poincaré. Poincaré worked on the three body problem. His crucial observation was that although it is impossible to precisely predict the trajectories of particles near the unstable Lagrange points, you can separate out families of trajectories that behave similarly. These similar trajectories together form the surface of a tube. A particle that starts out on such a tube will move along its surface, spiralling away from the Lagrange point. For each such out-bound tube, called an "unstable manifold", there is an in-bound tube, called a "stable manifold", along which particles move towards a region around the Lagrange point. Near each unstable Lagrange point, there is a multitude of such pairs of tubes, winding around each other in a very complex way, but ultimately going off into wildly different directions.Theoretically, a spaceship could hitch a free ride to the region close to the Lagrange point on an in-bound tube. More excitingly, what if an out-bound tube coming from the region around a lunar Lagrange point intersects an in-bound tube to a region around a Lagrange point of, say, the Sun-Jupiter system? Then a spacecraft could travel from one to the other practically for free, as long as it switches manifolds at the right moment.
I wasn't until the 1980s that the idea of exploiting manifolds for space travel was given serious consideration. But over the last few years, NASA mathematician Martin Lo and his team have built an elaborate theory around this idea. With increased computing power, these scientists used numerical experiments and did indeed find some such low energy paths. Each of these is like a valley carving through the potential energy landscape of the solar system. Spacecraft could flow along these channels practically effortlessly - barely needing thrusters to struggle against gravity.
Earth's Lagrange points are linked to those of Mars, or Saturn, by these minimal energy trajectories. Jupiter has Lagrange points associated with each of its many moons, all joined up into an interlinked web, which itself connects to the Earth system via the Jupiter-Sun Lagrange points. Spacecraft travelling along routes within this tube would be able to efficiently reach their destination. Any spacecraft that fly beyond the manifold, however, would enter the "unstable region" and their trajectory would inexorably stray further and further away from the low-energy tube. This collection of low-energy trajectory families spreads across the entire solar system, regularly interconnecting at Lagrange points into a vast system of tunnels. And the system is not stationary: the tubes forming the stable and unstable manifolds move with the planets, an ultracomplex heap of writhing interplanetary spaghetti.

Jules Henri Poincaré, 1854 - 1912.
This network is as ancient as the solar system, but is completely invisible and would have lain undiscovered were it not for the power of modern mathematics and numerical integration on fast computers. The mathematicians that discovered this system of low-energy trajectories have named it the Interplanetary Superhighway, or IPS.
The fact that the behaviour of trajectories near unstable Lagrange points is unpredictable, or chaotic, is only a minor nuisance for spacecraft stationed here. A total delta V of only a few m/s per year would be needed to keep nudging the space-station back towards the equilibrium point. But, according to Martin Lo, this inherent instability provides a remarkable opportunity for human exploration of the solar system
The Lunar Gateway
In chaos theory, systems like the LL1 Lagrange point are known as "highly nonlinear dynamical regions". If an object close to LL1 gets nudged , it will drift away, like the marble falling off the down-ward slopes of the saddle. Even a slight alteration to a trajectory passing close to LL1 will take it off into a different direction and lead to a large change in the eventual path of the spacecraft. This is more popularly known as the "Butterfly Effect" - in chaotic regions of space a small perturbation results in a huge difference in outcome.The upshot of all of this is that a spacecraft swinging past LL1 can easily push itself from one low-energy trajectory onto another that leads to a completely different destination. Thus a probe launched from Earth could, theoretically, be sent to LL1, fire its thrusters at a precisely calculated time, and efficiently switch from the LL1-EL2 tunnel into the one leading to Mars. The neighbourhood around LL1 is like a vast highway interchange, allowing spacecraft to choose between different IPS pathways. This means that a human habitat at LL1 could not only be used as a service-station for spacecraft needing repairs, but as a departures terminal for missions throughout the solar system. The space-station would very literally serve as the Gateway into the tunnel network of the Interplanetary Superhighway.
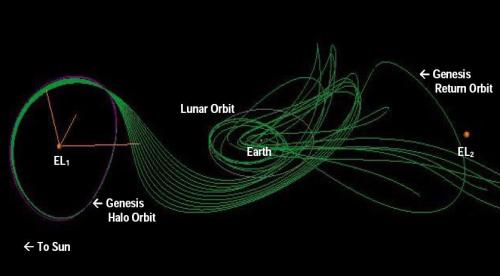
Figure 3: a perspective view of different paths through Earth's local IPS. The Genesis trajectory is only one of a large set of similar paths - it orbits EL1 five times, and returns to Earth via EL2. The other trajectories shown leaving EL1 each orbit the Earth in a different way, and some even interchange at the LL1 Gateway and exit the Earth-Moon system entirely - shown winding off past EL2 to the right. Image courtesy of NASA.
Ancient travellers
Genesis demonstrates well the power of mathematical analysis using computers and the advantages of chaotic regions. But it was not the first explorer, not by a long way, to have used the Interplanetary Superhighway. Some comets have been travelling along the ethereal tunnels for aeons, and the asteroid that wiped out the dinosaurs 65 million years ago is believed to have reached Earth through the IPS. For some scientists, these near-Earth asteroids present as much of an opportunity as they do a threat. Many scenarios of dealing with such a potential killer involve trying to destroy it with nuclear weapons or landing rockets to push it away into a wider orbit. But using the nonlinear dynamics of the IPS such passers-by could be captured and parked in an orbit around one of the Lagrange points. Such a huge lump of iron would provide humanity with an enormous supply of raw materials for space industrial complexes.This newly found Interplanetary Superhighway is a perfect example of the overlap between classic analysis and modern numerical techniques. The genius minds of Euler and Lagrange used the new technique of calculus to solve the restricted three body problem and show the existence of these intriguing equilibrium points in space. Now, 200 years later, we are employing our own ground-breaking methods using dynamical systems theory and supercomputers, and taking our first steps along the invisible tunnels stretching through the solar system.
Further reading
- This page by John Baez contains more information on Lagrange points.
- This article by Neil Cornish gives a technical derivation of the positions of Lagrange points.
- The article "The Interplanetary Superhighway and the Origins Program" by Martin Lo describes the IPS and some of the maths behind it.
- Wikipedia's entry on the IPS has a long list of references.
About the author

Lewis Dartnell read Biological Sciences at Queen's College, Oxford. He is now on a four-year combined MRes-PhD program in Modelling Biological Complexity at University College London's Centre for multidisciplinary science, CoMPLEX. He completed the MRes last year, and is now just beginning a PhD in the field of astrobiology. He is using computer models of the magnetic fields on Mars to predict radiation levels, and whether alien life, or even future human explorers, could possibly be surviving near the surface.
In 2003 he came second in the THES/OUP science writing competition, and in 2004 was awarded second prize in the Daily Telegraph/BASF Young Science Writer Awards. You can read more of Lewis's work at his homepage.
Comments
Anonymous
Thank you for this very well written article. However, I found the explanation centered around Figure 1 confusing as, oddly, Figure 1 does not actually have the moon in it.
Marianne
Yes, that's a bit confusing. The Moon is actually there but it's not very visible. It sits on the circle around the Earth, right in-between LL1 and LL2.
Anonymous
I didn't spot it at first either, not help by the fact that like the Earth the day seems to be facing away from the sun! I found it more confusing that the labels for the points changed between the diagrams.
All that said, very good article.
Anonymous
For someone getting his PhD in Applied Mathematics/Celestial Mechanics at the time of the first lunar landings, coming back to Halo Orbits after decades was a reall "eye-opener"! Yes, we had heard of Ljapunov stability and the fact that Henri Poincaré had forseen various "celestial mechanics wonders", but our computers at the time of Apollo were adequate for integrating Hill type orbits, but not for large scale numerical experiments with halo trajectories! While reading, your article unleached a myriad of ideas in my brain, connecting the special case of fast "swing-by-orbits" and the generalized case of flying between Libration points. Thanks!
Your love for interdisciplinary thinking connects us even further than Celestial Mechanics - astrobiology is another subject that shows we live at just the right time. Well, having passed 70...
Best regards
Bruno Stanek
www.Stanek.ch
Matthew
Well done and congratulations on such a well written article with an excellent explanation of the Lagrange points. Humans are entering an exciting time in Maths and Science and will only move forward from here. Your work and the work of others are truly respected!
Bill Filson
Thank you for clear description of Lagrange points.
I'm now enlightened and you have given me an understanding gravitational topology and its amazing usefulness to space exploration. Not to dismiss the dangers of random large space objects being 'funnelled' dangerously toward us and the possibility of cleverly 'bumping' them into a stationery position to mine their valuable mineral content. Mathematics is wonderful. Thanks also to the brilliance of Lagrange.