Plus Advent Calendar Door #5: Five won't fit

Triangles do it, squares do it, even hexagons do it — but pentagons don't. They just won't fit together to tile your bathroom wall. That's the reason why you'll find it very difficult to find pentagonal tiles in any hardware shop.

It's actually really easy to see why pentagons won't tile the plane. We are talking regular pentagons here, shapes that have five sides of equal length and angles between them. In a regular pentagon the internal angle between two sides is 108°. In a regular tiling, adjacent tiles share whole edges, rather than just parts of edges, so corners of tiles meet corners of other tiles. To fit a number of tiles around a corner point, their internal angles must add up to 360°, since that's a full turn. If you try to fit three pentagons, you only get 3 x 108° = 324°, so there is a gap. If you fit four pentagons, you get 4 x 108° = 432°, so two of them overlap. The same isn't true for equilateral triangles, squares, or regular hexagons. Here the internal angles are 60°, 90° and 120° respectively, so you can fit six triangles, four squares and three hexagons around a corner point. (You can try and work out for yourself if any other regular polygons can give you a regular tiling.)

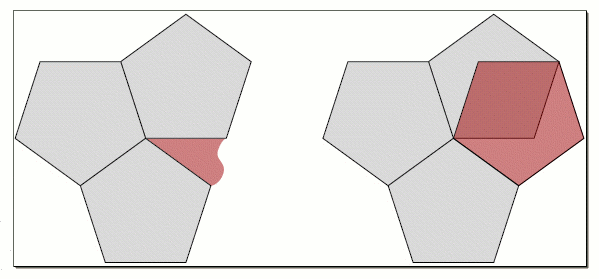
Three pentagons arranged around a point leave a gap, and four overlap. Image: Craig Kaplan.

If pentagons don't work can we perhaps use other shapes with five-fold symmetry to tile the plane? Find out more in The trouble with five.

Return to the Plus Advent Calendar