The point (0.25,0.25) lies on the outline curve
In our approximation of the outline curve, which comes from only finitely many chords, every chord contributes an interval, namely the one marked out by its intersection points with two adjacent chords. As we add in more and more chords and get closer and closer to the outline curve, these intervals become shorter and shorter, as intersection points move nearer to each other. In the limit, when there are infinitely many chords, these intervals have shrunk to points. Thus, every chord contributes exactly one point to the outline curve. Also note that the outline curve is symmetric with respect to the line
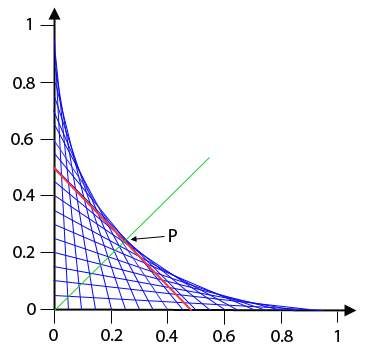
The red line is L0.5 and the green line is the symmetry axis L.