
The puzzle of time

What is time?
One thing that's painfully clear to all of us is that time has a direction. It marches onwards with horrifying regularity and there is no way of turning it back. From a physical viewpoint, this direction of time presents a puzzle, because it's not there in the fundamental laws of physics. Resolving this riddle is a task, not just for physicists, but also for philosophers. In May 2012 we went along to a conference on the philosophy of cosmology in Oxford, to witness representatives of both creeds grapple with time. We spoke to the eminent Roger Penrose, and the no less illustrious philosophers of physics Jeremy Butterfield and David Wallace. You can listen to the interviews in our podcast, but if you prefer your words on a page, keep reading.
Will we ever know?
The Oxford conference was part of an ongoing series of events, collectively entitled Establishing the philosophy of cosmology. It's intended to remedy the fact that few philosophers choose to engage with that most encompassing of scientific disciplines. Yet, perhaps more than any other discipline, cosmology needs philosophy. Cosmology not only pushes the boundary of known physics, it also raises the question of how much understanding we can actually attain. Are we even capable of conceiving of a theory that explains everything there is to know about the Universe?
The truth is that we don't know. There is a mathematical result, called Manchak's theorem, which states that it is impossible to know everything about the nature of the Universe. The gist of the theorem is that you can only observe things that are in the past, and out of these past things you can only observe those that don't require information to travel quicker than light for you to make your observation — that's because, as Einstein recognised, the light provides a universal speed limit. "This means you can only observe things in your so-called past light cone," explains Butterfield. "The collection of all spacetime that is able to send you a signal, which travels at most as fast as light. If you take due allowance for that limitation, then even if you had full knowledge of your past light cone, you wouldn't know about the global shape of spacetime. [Manchak's theorem] is a theorem of sadness and pessimism."

Jeremy Butterfield.
But then, what's the point of cosmology? Is it even worth the effort? "You have to just steel your heart and soldier on. We must be able to somehow get through the tunnel," says Butterfield, pointing to scientific realism as the saving grace. "In philosophy, realism is a very broad doctrine going back over the hundreds and thousands of years. [It holds] that reality is independent of our human imagination and our minds. [It] goes on to say that, although reality is separate from us, we can have knowledge of it. So realism is an optimistic doctrine. Reality is different, but don't be despairing, we can get knowledge of it. Scientific realism is the modern version of that within twentieth century philosophy. Because the enormous success of science prompts the thought that it is science that gives us the knowledge of reality."
This still leaves us with the problem of deciding which scientific theories to believe. When should we declare ourselves satisfied with the evidence for or against a theory? "That is a very difficult question, doubly difficult," he says. "I don't think there are general rules. There can't be general rules that are the same in different sciences, or even different episodes in one science. But I certainly do think that [there is enough evidence] for things like the history of the observable Universe: the existence of some primeval fireball, the creation of nuclei of elements in the very first seconds, and then the formation of stars and galaxies by gravitational clustering. Those are things that we do have so much and such varied evidence for, that as a scientific realist I would say we know them now and will never give them up. We know them just as much as we know that oceans have water in them."
The arrow of time
Equipped with Butterfield's optimistic realism we can return to the problem of time. Why is the direction of time such a problem for physicists? "If you look at the physical processes in the world around us, most of them seem to have a rather definite direction; a difference between the past and the future," explains David Wallace. "For instance, ice cubes melt, but we don't observe water spontaneously forming ice cubes. That might just seem like a basic feature of physics. But the slightly strange thing is that the microscopic physics, the physics of the individual atoms and molecules, that supposedly make up those ice cubes and other big systems, don't seem to have that property. They don't seem to have in their physics any difference between the past and the future. If I showed you any large scale process and I videoed it, and then I played you the video again backwards, you would be able to tell immediately which way I played it. If I did the same for the microscopic physics of individual small systems, you wouldn't be able to tell. Since we think that the principles of large scale physics come out of the principles of small scale physics, there seems to be a bit of a problem, and we want to understand how that can be resolved."

David Wallace.
The branch of physics that smoothes the path from small to large scale processes is called statistical mechanics. As the name suggests, it's about letting go of the individual atoms and molecules and instead looking at their bulk behaviour. Things like the temperature or pressure of a gas are treated by statistical mechanics — neither exist at the level of individual atoms, they arise as a property of the gas as a whole. Statistical mechanics has been around for 100 years and it's been very successful. "We can more or less calculate what the heat capacity of an ice cube is, how quickly it melts," says Wallace. "We can do that for a whole bunch of physical systems and we learn how to do it for more every year."
"But precisely because we've somehow gone, through statistical mechanics, from the microphysics that doesn't care about time direction to the macrophysics that does care about time direction, somewhere in statistical mechanics, explicitly or tacitly, we're making an assumption." The assumption breaks the symmetry of time and somehow puts in the fact that the past and the future are different.
Just what that assumption might be, though, is the million dollar question. "Statistical mechanics is one of these areas in physics whose machinery we know how to use very, very well," explains Wallace. "But there are a lot of deep controversies about how to understand what that machinery is doing, what justifies certain mathematical moves and so forth. The subject, if you like, was conceived in sin. We've had these foundational, conceptual problems in it ever since the late 19th century, when the theory started to be written down. In a sense we've got much, much better at calculating within the theory since then and we've illuminated various of these controversies, as to what the underlying time asymmetric assumptions are. But illumination isn't the same as getting a complete solution, many of the problems still remain."
Big Bang statistics
The closest cosmologists have got to a solution to this problem involves that primeval fire ball, the Big Bang. Its connection to statistical mechanics lies in a central result of the latter, known as the second law of thermodynamics. When you look at a physical system, for example a gas being released from a bottle into a room, you can ask how much randomness or how much disorder there is in the system. In the gas example, the initial situation, which has all the atoms of the gas trapped in the bottle, is more orderly, so it's less random, than what you get after the gas has escaped and all the atoms are randomly dispersed throughout the room.
There is a number that measures the randomness or disorder in a system; it's called the system's entropy. The second law of thermodynamics states that the entropy of a closed system never decreases, in fact it usually increases. Things move from order to disorder. We see this law in action all the time. In the gas example the entropy increases as the gas disperses. Similarly, you can turn an egg into a much less ordered omelette, but you can't turn an omelette back into an egg. And you can easily turn a glass of wine into a mess on the carpet which is extremely unlikely to ever reform itself into a tempting beverage.
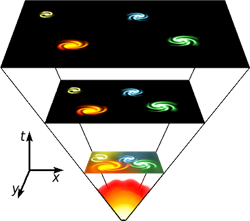
Cosmologists believe that our Universe started with the Big Bang around 13.7 billion years ago and has been expanding ever since.
The problem with time is reflected in the asymmetry of this law. "Most laws of physics, such as energy conservation and the dynamical laws, work just as well in the forward direction as in the backward direction," explains Roger Penrose. "What's rather strange about the second law is that it's a one directional law, so people try to understand how that can come about, by all sorts of considerations."
One important consideration is that the physical systems we perceive to have a direction in time all start out in a highly ordered, low entropy state. In the omelette example molecules start out neatly separated into egg white and egg yolk and they end up all mixed up. If you count all the configurations of molecules that are possible, you'll see that there are many, many more that have them all mixed up than there are configurations that have them separated out into white and yellow. Therefore, the system is much more likely to evolve into a mixed up, higher entropy state than it is to evolve into a lower entropy state. The second law of thermodynamics is a statistical law: it's not impossible for egg yolk and white to spontaneously re-assemble, it's just highly unlikely. The apparent arrow of time emerges as a property of the macroscopic system, even though it's not there in the laws that govern the individual particle interactions.
Applying this reasoning to the whole Universe leads to the conclusion that the Big Bang must have been highly organised. This seems weird at first since order isn't something we associate with an explosion of an infinitely dense and hot particle soup. But Penrose suggests that at the very start the Universe was highly uniform in a gravitational sense — matter was evenly distributed throughout and only later did gravity clump things together into stars and galaxies. In fact, he suggests that gravity wasn't even activated at the Big Bang. Einstein's general theory of relativity contains a mathematical term which corresponds to the gravitational field and Penrose postulates that this term was zero at the Big Bang. In this sense, he suggest, did the Universe start out in a low entropy state.
The cyclic universe
But this leads to another question: why? Out of all the possible states the Universe could have started out in, the highly ordered ones are incredibly rare. So short of evoking a creator, who has purposefully chosen this state, how can we explain the low entropy beginning? Penrose has his own controversial and highly mathematical theory. We accept that our Universe started with a Big Bang and that at the Big Bang it was infinitely compressed, hot and dense. We also know that our Universe is expanding; in fact, the rate at which it is expanding is accelerating. If this continues, then in the remote future the Universe will have expanded out to infinity and its density and temperature will have vanished to nothing.

Roger Penrose.
On the face of it the Big Bang and the fully expanded Universe appear radically different. But Penrose argues that in both situations the Universe is actually insensitive to the very features that make them so different, namely distance and time. All this can be formulated in stringent mathematical terms and mathematically you can actually identify the two situations. Then our Big Bang simply becomes the end of a previous universe.
"[This] is a rather radical view of cosmology, in which the Big Bang was not the beginning; that there was a previous aeon," he explains. "The aeon [is] what we presently regard as our picture of the entire history of the Universe. So our present aeon starts with a Big Bang and ends with this exponentially expanding universe. Then I say there was a previous aeon also, and it will keep on going, there's one after ours and one before that one and so on. The previous aeon was what happened before the Big Bang."
Penrose's theory hinges on the idea that at both ends of an aeon, at the big Bang and in the fully expanded Universe, the masses of particles are irrelevant. "As you get to higher energies, higher temperatures, the mass is completely gone. At the remote end of the future, you have a somewhat similar situation. The mass goes away and you have effectively nothing left but photons." Penrose has formalised this idea within the language of Einstein's general theory of relativity. "That needs some serious mathematics, but the idea is, in sort of hand waving terms, that the scale becomes unimportant. So the Big Bang of our aeon is the development of this remote future of the previous aeon."
Penrose's cyclic universe model gets around the puzzle posed by the low entropy beginning: the Universe wasn't simply presented to us in this state on a plate, rather it evolved from the previous aeon. It's an idea that sounds pretty fantastical and it's highly controversial among cosmologists. But Penrose claims that it can be tested in experiments and that some experimental evidence for it already exists. You can find out more about this model in Penrose's book Cycles of time.
Further reading
Find out more about time in this Plus article.
About the author
Marianne Freiberger is editor of Plus.
Comments
happyspoon
I don't really understand their points, and I am really curious about the beginning of our world.
But do the professors mean that Einstein's theory is not correct totally? so interesting!
Anonymous
It is not that Einstein's theory is not correct because it is.
One of the premises is however wrong.
Neither Einstein nor anybody else in those days suspected that time (as we generally think about it) does not exist.
However as J.M.E. McTaggart showed back in 1908 when he published hit proof of the unreality of time, that is actually the case.
McTaggart used logic I found out by trying to understand time and motion.
Have a look at http://www.spacetime.nu where I am trying to explain how it could work.
BN
Anonymous
Philosophy of Time
The nature of time has had extensive attention in part down through the ages, such as Plato, St. Augustine, Pascal, Leonardo, Newton etc. For example, Newton considered time to flow uniformly, as if it were a separate manifold (1-surface) from the 3-surface of his mechanics described universe.
‘Absolute, true, and mathematical time, of itself, and from its own nature, flows equably without relation to anything external…’ Newton’s Principia
For a 3-manifold, this would give a product space description M^3 x M^1, the simplest fiber bundle description. Hence such description would be universal; that is the same common time for throughout the universe. Subsequently, the relativistic model refers to time as the interval between events, wherein clocks are associated with respective observers. However an event such as the Big Bang, and concomitant Big Expansion of our manifold (i.e. 3-surface), does not have such a General Relativistic Theory description; nor is ‘initial’ 3-expansion (i.e. Hubble expansion, Hubble parameter) of our 3-volume limited by velocity of light, as in Special Relativity. Hence the possibility of further modeling in regards to how our 3-space and contents evolves.
Might there be another common time description as to how our 3-volume evolves? Just as Gauss described curvature of a surface intrinsic to such 2-surface, and Riemann described curvature of a 3-surface as intrinsic to such 3-surface, might not one analogously describe time as intrinsic to our 3-surface?
Could the non-linear Hubble expansion be utilized as such common time description for our 3-surface, and perhaps for a set of such 3-surfaces (i.e. 3-volumes, 3-manifolds); that is for the, misnomer ‘multiple universes’? Universe, denotes all inclusiveness, rather than multi-universe which implies a set of such all inclusiveness. Hence better to refer to a set of 3-volumes i.e. 3-manifolds. Also non-linearity to Hubble expansion might even be always of an exponential nature, and may be just a specific example of the more general case: all explosiveness is of an exponential nature.
So do all locations of our 3-volume, and for a possible set of 3-volumes, share the same common time i.e. cosmic time? That is, perceiving the same Big Bang ~13.8 billion years ago; and thus the same ~2.7 degree kelvin temperature of cosmic background radiation?
Also for a set of 3-volumes, contained in an array of planes, spherically symmetrical about a modified central force, might one also have a concomitant common cosmic time description intrinsic to the System i.e. array of planes consisting of 3-volumes? That is, might one utilize the construct of a spherical shell through the respective centers of all 3-volumes, denoting such common cosmic time for all 3-manifolds? This might be referred to as Modified Global Simultaneity (MGS) construct. Such set of successive MGSs would be matched to the integers; hence having positive definite separation. And such set of MGSs could be rendered as always exponentially changing; part of an exponential curve. Likewise for the changing rate of Hubble expansion, intrinsic to each and all 3-volumes.
Thus in such modeling, one would have two concomitant descriptions of an overall common cosmic time; the Hubble Expansion, intrinsic to 3-volume, and MGS, intrinsic to the System.
Further elaboration https://sites.google.com/site/zankaon/
Anonymous
In the "Big Bang statistics" section, after defining entropy it is said that the entropy of a system never decreases, but the second law of thermodynamics states that the entropy of the UNIVERSE never decreases, not the system. The entropy of a system can decrease.
Marianne
Yes you are right - it should have said that the entropy of a closed system never decreases. We have fixed the mistake. Thanks!
Anonymous
How can you really be sure that time is just going in one direction? Does time even exist? Is it just a man made measure? What is time, really? In my opinion time is a limitation, invented to control people. If time did not exist and if time was not in our consciousness then our minds would not be limited by time and, then just imagine what possibilities there could be? Perhaps the one reason why we can't go forward or backward in 'time' is because it is in our consciousness that time is linear. If time did not exist then we might be able to travel to a different moment in a different dimension? I also think that if we were not bounded by time, humans would follow their inner sense of timing as do the animal and plant kingdoms, think how much we would be in sync and in flow with each other then!