
The story of the Gömböc
This article is also available as a podcast.
A Gömböc is a strange thing. It looks like an egg with sharp edges, and when you put it down it starts wriggling and rolling around with an apparent will of its own. Until quite recently, no-one knew whether Gömböcs even existed. Even now, Gábor Domokos, one of their discoverers, reckons that in some sense they barely exists at all. So what are Gömböcs and what makes them special?
Balancing act
The defining feature of a Gömböc is the fact that it's got just two points of equilibrium: one is stable and the other is unstable. If you put a Gömböc down on a flat surface, resting on its stable equilibrium point, it will stay as it is. "Even if you kick it a little, it will come back to its resting position at the stable equilibrium point," says Domokos, a mathematician at Budapest University of Technology and Economics. "The other equilibrium point is unstable. You can balance the Gömböc at this point a bit like you can balance a pencil on its tip: the slightest push will make it fall over." It's impossible to balance a Gömböc on any other point: if you try, it will move off in a specific direction. That's why the Gömböc seems to have a life on its own: put it down at a non-equilibrium point, and it will start rolling around in a systematic way until it has reached the stable equilibrium position. In other words, the Gömböc is self-righting.

A Gömböc made from plexiglass.
"It's a bit like putting a ball on a hilly landscape," says Domokos, "if you put the ball down at a generic point, it will always roll off in the same direction, down into the valley. If you put it on a hill top, it will also roll off, but the direction depends on the direction in which you kick it — that's the unstable equilibrium. Put it in the valley, and it will not roll off at all — that's the stable point of equilibrium."
To give it its full mathematical description, a Gömböc is a three-dimensional, convex and homogeneous object with exactly one stable point of equilibrium and one unstable point of equilibrium. Requiring it to be homogeneous amounts to saying that you're not allowed to cheat: the material from which the Gömböc is made has to be uniform throughout, so you're not allowed to use weights, as those found in roly-poly toys, or other irregularities to get the Gömböc to self-right. Convexity means that the Gömböc is not allowed to bulge inwards, in other words, the straight line connecting any two points on the Gömböc has to lie entirely within the Gömböc. It's easy to create a non-convex shape with one stable and one unstable equilibrium point, hence the restriction to convexity.
Doubtful existence
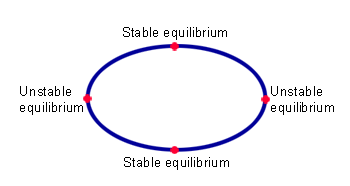
An ellipse has two stable and two unstable points of equilibrium.
The reason why many people thought that Gömböcs didn't exist is that in two dimensions there is no convex shape with only two points of equilibrium. "Imagine you have a shape made from plywood," says Domokos, "which is moving between two vertical glass plates. Then the shape would balance at some points. An ellipse, for example, would balance at the centres of its two 'long sides' — these are the stable equilibrium points — and at the centres of its two 'short sides', these are the unstable points." A square can balance on the centres of its four sides, the stable equilibria, as well as on each of the four vertices, though rather precariously, making the vertices unstable equilibria. Similarly, an n-sided polygon has n stable equilibrium points — the centres of its sides — and n unstable ones — its vertices.
It turns out that two stable and two unstable equilibrium points is the best you can do in two dimensions, and it's relatively easy to prove this. The proof basically amounts to showing that a convex shape with just one stable and one unstable equilibrium point makes impossible demands on its centre of gravity (see here for some more detail).
Many mathematicians, including Domokos, concluded that the same result should hold in three dimensions, and they set out to prove it. "The fact that no-one could imagine a three-dimensional shape with just one pair of equilibrium points suggested that it would be worth-while to disprove its existence," he explains. "I tried to do this, unsuccessfully, for a very long time. Then I had a conversation with [the Russian mathematician] Vladimir Arnold, in which he expressed the view that such a shape might exist after all, despite all the rumors going around that it didn't. This made me think in a different way, and I soon realised that the problem was much more beautiful than I had thought at first."
A geometric stem cell
The beautiful fact that Domokos discovered, with the help of his colleague Peter Várkonyi, was that a Gömböc, if it existed, would be a sort of stem cell from which you could "grow" three-dimensional shapes with all other configurations of equilibrium points.
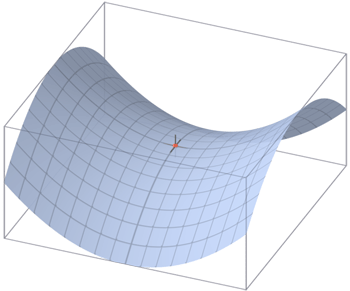
If you balance a marble at a saddle point, the balancing act is stable in one direction and unstable in infinitely many other directions.
In three dimensions, stable and unstable points are not the only equilibrium points: you can also have saddle points. If your object is balanced on a saddle point, then the balancing act is unstable in infinitely many directions — if you push your object in any of these directions it will topple over — and stable in exactly one direction — if you give it a slight push in that direction, it will come back to the equilibrium point. This is similar to a marble balancing on the mid-point of a saddle. You can make it roll down the sides of the saddle in infinitely many directions, but if you push it exactly along the line running from the front to the back of the saddle, something that's admittedly quite hard to do, it will roll back to the saddle point.
For a convex and homogeneous three-dimensional object, the number of saddle points depends on the number of stable and unstable equilibria: if the object has i stable and j unstable equilibria, then it has i+j-2 saddle points. You can prove this fact mathematically, and it's known as the Poincaré-Hopf theorem. Inspired by this nice relationship, Domokos set out to classify three-dimensional shapes according to their number and type of stable and unstable equilibrium points: given numbers i and j, which objects, if any, have i stable and j unstable points of equilibrium (and therefore i+j-2 saddle points)?
"It was not known if there were objects for each category [formed by an (i,j) pair]," says Domokos. "But we did have some examples. The cube, for example has six stable points of equilibrium [the centres of the six faces], eight unstable points [the eight vertices], and twelve saddles [the centres of the twelve sides]. We also knew about the tetrahedron and many other objects, but there are infinitely many categories. Then we realised that it is always possible to increase the number of equilibrium points by one using a small perturbation." In other words, a small but purposeful deformation of the object would give rise to one extra equilibrium point.
"This is intuitively clear," says Domokos. "If you go on a hike and need to collect some water, then you can dig a small hole, and water will collect in that hole. So with a very small perturbation you have produced a stable point of equilibrium. However, the opposite is not true: getting rid of a lake [which contains a stable equilibrium point] is no easy job. Similarly, if you have an object, it is generally not easy to get rid of an equilibrium point, but it is possible to create one." Domokos and Várkonyi found an explicit algorithm telling you exactly how to endow a convex and homogeneous three-dimensional shape with an extra equilibrium point.
This result was momentous as far as the not-yet-discovered Gömböc was concerned. "It told us that if you had an object [with the minimal number of equilibrium points, one stable and one unstable], then this would prove that objects exists in all other classes too, because you can increase the number of equilibrium points one by one. So this object would be like a stem cell: you could derive the existence of all other categories from it, but you couldn't derive its existence from bodies with higher numbers of equilibrium points. Mathematics is all about beauty, and this result is very beautiful."
Mathematical field work

Pebbles from beaches on the island of Rhodes. The left pile contains convex pebbles and the right pile contains concave pebbles.
But despite this tantalising beauty, Domokos and Várkonyi's attempts to prove the Gömböc's existence remained futile, so Domokos took a desperate measure. On a holiday to a Greek island he and his wife collected and inspected 2000 beach pebbles in the hope that they might find one behaving like a Gömböc. It was a strenuous effort, which a weaker relationship may not have survived, and it failed. "We learned very interesting things from a pebble point of view, but nothing from a Gömböc point of view," says Domokos. "We were tired and depressed. When you looked at these pebbles you got the feeling that even if you went to all other Greek islands, you would never find [one behaving like a Gömböc]. But why not? If this type of pebble doesn't exist, then there must be a mathematical reason for this."
This line of thought led to an important insight into the Gömböc's nature: Domokos and Várkonyi realised that a Gömböc, if it existed, could not be very flat, or very thin. A flat object, like a frisbee, generally has two sides, and contained in each there'll be a stable equilibrium point — that's one stable equilibrium too many for a Gömböc. A thin object, like a pencil, will generally have two unstable equilibrium points at its two tips, so it cannot be a Gömböc either.
The perfect figure

Thin objects like this pencil generally have two unstable points of equilibrium at their tips, while flat objects, like these pebbles, generally have two stable points of equilibrium.
Domokos and Várkonyi made their intuition precise by giving a formal mathematical definition of what they meant by flatness and thinness, each measured by a number greater than or equal to 1. They then proved that a Gömböc's flatness and thinness both have to be equal to 1, that is, both values have to be as small as is possible.
The result gives some insight into why the Gömböc is only just teetering on the brink of existence. If you make a Gömböc just a tiny little bit thinner or flatter, then its flatness and thinness values aren't minimal anymore. So according to the result, the object stops being a Gömböc — it must have gained extra equilibrium points, or stopped being convex.
The Gömböc's sensitivity to change means that a Gömböc-like pebble can only exist for a short time on the sea shore before other pebbles, moved by the sea, start chipping away its Gömböc-ness and turn it into an ordinary pebble. "It's a fundamental question," says Domokos, "to which you expect a clear-cut answer: something should either exist or not exist. But in the case of the Gömböc, the answer is that it does exist, but barely so. If you drop it, it ceases to be what it was, so physically, it is a very fragile existence."
Finally, a Gömböc!
Having thus explained why they had not been able to find a Gömböc on the beach, Domokos and Várkonyi drew new hope and tried a new line of attack in their search for a proof of its existence. In two dimensions a Gömböc is impossible because it needs a balancing that would require the centre of gravity of the shape to be in two places at once. But in three dimensions there is more space to balance things out, so Domokos and Várkonyi started tinkering around with various shapes until they had a description of an object with all the required Gömböc properties.
Many mathematicians would have stopped there — if you can prove that something exists, then why go on to build it? — but Domokos and Várkonyi wanted their very own Gömböc to take home. This proved difficult, as their initial construction was too close to an actual sphere. "The deviation from the sphere was only 10-5," says Domokos, "so with [a diameter of 1m], the object would differ from a sphere by a only hundredth of a millimeter." This surpasses the precision of even the most sophisticated tools. If you try to manufacture such a Gömböc, all you'll ever get is to all intents and purposes an ordinary sphere.
The problem was that Domokos and Várkonyi had wanted their object to be as smooth as possible, avoiding sharp edges as far as they could. It was only when they let this requirement go that they came up with a new and buildable version of a Gömböc. That's the version you can see in the pictures — note the sharp edges. But even this buildable version requires an incredible level of precision: the Gömböcs are now being manufactured using computer controlled machining with precision tolerances below 10 microns — that's about a tenth of the thickness of a human hair!
Gömböcs in nature
While the Gömböc made a good job of hiding from mathematicians, it didn't escape the penetrating gaze of evolution. Thinking that Gömböc-like shapes must appear somewhere in nature, Domokos turned his attention to tortoises. Being turned on its back is a potential disaster for any tortoise, so much so that the males in some species try to turn over their rivals during their battles for females. So any tortoise that's able to struggle back on its belly has an evolutionary advantage. Some species of tortoise manage to turn themselves back over using their muscular necks as a lever, while many others can't self-right at all.
Domokos started an extensive search in pet shops and zoos, turning over tortoises while their owners weren't looking, and finally found what he wanted: "Suddenly one day I came across the first little tortoise that was doing exactly what it was supposed to do," he recalls, "it was acting like a Gömböc!" The shell of this high-domed species is similar to a Gömböc — it contains no stable equilibrium point, so when an individual is put on its back, it automatically flips over into the only stable position: lying on its belly. Domokos conducted an extensive study of tortoises using a complex three-dimensional model of their shell, and identified two species, the Indian star tortoise and the radiated tortoise, which use their Gömböc-like shells to self-right. The results of his research were eventually published in the biological journal Proceedings of the Royal Society B in a paper co-authored by Várkonyi, and biologists have accepted that the Gömböc-like shells are indeed a result of natural selection in favour of the ability to self-right.
The Gömböc adventure has led Domokos to look deeper into the evolution of shapes in general. He's currently developing ways of deducing the habitat of a tortoise from the shape of its shell, a project that will enable scientists to learn more about the living spaces of extinct tortoises, of which only fossilised shells remain. He's also developed a model which explains how asteroids, that aren't round like planets, but have sharp edges and flat areas, evolve their shapes (the paper has been published in The Astrophyiscal Journal).
So the Gömböc, which started out as a question in the mind of a mathematician, not only exists in the abstract, but also in nature. And who knows what lies ahead of it in terms of human-made applications? For the moment, though, the Gömböc is being produced for purely aesthetic reasons, and enthusiasts can purchase their very own model on the Gömböc website. And if you find yourself close to Cambridge, you can come and admire a real Gömböc at the Whipple Museum of the History of Science, to which it was donated by Domokos and Várkonyi in April this year.
For a more technical look at the topics covered here read Domokos and Várkonyi's articles Mono-monostatic bodies: The answer to Arnold’s question and Static equilibria of rigid bodies: dice, pebbles, and the Poincaré-Hopf theorem . To hear Domokos himself speak about the Gömböc, listen to the podcast accompanying this article.
About this article

Gábor Domokos

Péter Varkonyi
Marianne Freiberger, Co-Editor of Plus, interviewed Gábor Domokos in Cambridge in May 2009.
Comments
Anonymous
This was such a great work! Enjoyed reading every single bit of it! Now all I need is a Gömböc!
Was just thinking why is a Gömböc called so? What is the root of this word?
Rick
It's a Hungarian word for sphere or orb.
Anonymous
Why would a sphere drawn out to a single point not be a gomboc? A 3D shape with a 2D profile something that looks a bit like this....... C>
Its stable equilibrium would be the furthest position on the sperical half of the shape from the point. The unstable equilibrium point would be the point itself. Just a thought. I'm sure I'm missing something.
Fascinating article!
Jonathan
Anonymous
Because your object would have infinite stable points, it would just rest on its side C> along one of those edges... It would only stand up if the bottom of that C shape was weighted...