
Why you shouldn't use a toss for overtime
When a tied game in professional soccer leagues (football in most of the world) goes into overtime in knock-out tournaments or cup competitions, a coin toss is used to determine which team starts a sequence of penalty kicks to break the tie. Similarly, when a tied game goes into overtime in the National Football League (NFL) in the United States, a coin toss is used to determine which team starts as offence and which starts as defence in the overtime period.
In both sports, we claim, a coin toss is a flawed system for making choices that can significantly affect who wins. Because we are more familiar with American football, we will focus on this sport, but we return later to the case of soccer.
We argue that there is a superior system for determining a winner in both sports, based on bidding. It is related to a method used in fair division: when dividing a cake, one person cuts the cake and the other chooses the piece he or she prefers.
The problem in the NFL

In the NFL a coin toss decides who plays offence and who plays defence. Image: Pierre-Selim.
In the NFL tossing a coin to determine who kicks and who receives in overtime seems eminently fair before the toss, but after the toss there is a problem. Although the outcome of the coin toss is fair—both teams are equally likely to win—after the toss the winner enjoys a distinct advantage when it invariably elects to receive and play offence. By doing so, between 1994 and 2011 the receiving team won nearly 60% of the overtime games, 34% on its opening drive.
Beginning in 2012, the NFL attempted to ameliorate this problem by precluding the receiving team from winning a game with a field goal (three points), as opposed to a touchdown (six points), on its opening drive. That is, it had to score a touchdown to win immediately. But after the opening drive, a game would end in sudden death—the team that scored first won.
When this rule was used for the first time in the 2011-2012 playoffs, the two games that ended in ties were both won by the team that won the coin toss. In the 2012-2013 season, there were 23 overtime games (about 8% of the total), one of which ended in a tie. Of the 24 nontied overtime games played so far under the field-goal exclusion rule, 16 (2/3) were won by the receiving team and eight (1/3) by the kicking team, despite the new field-goal exclusion rule. In other words, the winner of the coin toss enjoyed, on average, a 2:1 edge in overtime.
Bidding on a starting line: A win-win solution
We believe a more radical solution is called for that takes chance out of the picture. The rule change we recommend more than levels the playing field by making each team more satisfied with its position than if it were in its opponent's position.
Call a rule fair if it is one in which each team, whether it is offence or defence at the start of overtime, prefers its role to its opponent's role by the same amount. When this is the case, each team thinks it is actually at an advantage vis-à-vis its opponent.
How is this possible? Our solution is based on the same principle that leads to the satisfaction of a buyer and a seller when they reach an agreement on the selling price of a good. Because the two parties prefer different things—the buyer prefers the good to the money, the seller the money to the good—the transaction is a win-win outcome.
Instead of bargaining with money, we propose that football teams bargain over the yard line from which play starts by bidding on its location. There would not be the usual kickoff at the start of overtime but, instead, play would commence at a particular yard line. The yard line selected will be the average of the teams' bids, with the low bidder (in a sense that will become apparent in a moment) playing offence and the high bidder playing defence. This outcome will be one that each team prefers, and by the same amount, to that of being in the position of its opponent.
To illustrate, assume that team A bids the 20-yard line, which means that
- it is willing to play offence from its own 20-yard line, so it would need to move the ball 80 yards to score;
- it is willing to play defence from its opponent's 20-yard line, so its opponent would need to move the ball 80 yards to score.
We call this the indifference point of team A, because playing offence from its own 20-yard line, or defence from its opponent's 20-yard line, is the point at which it regards the chances of its winning to be equal (though not necessarily 50-50—this will depend on the relative quality of the teams). We presume that every team has an indifference point, which may be different against different opponents (depending on their strengths and weaknesses).
To continue our illustration, assume that team B's indifference point is the 30-yard line. Averaging the two bids yields the 25-yard line, from which A will play offence (because having bid 20 it is the low bidder) and B will play defence:
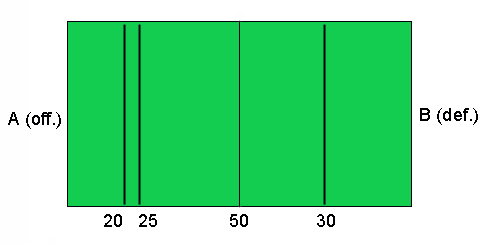
When play starts, note that A, as the offensive team, is 5 yards closer to B's goal line (and scoring) than its offence indifference point of 20 yards, because it needs to move the ball 75 instead of 80 yards. Likewise, B is 5 yards farther from its defence indifference point of 30 yards, because it needs to prevent movement of the ball by 75 rather than 70 yards.
Thereby each team gains by the same amount over its bid (5 yards). Not only is this a win-win solution for the teams, but it is also fair—each team prefers its position to its opponent's position, and by the same amount: if team A were in team B's shoes, it would have to play defence from its opponent's 25-yard line, when in fact it prefers to play defence from the opponent's 20-yard line. Similarly, team B prefers its position to that of team A by five yards.
If both teams make the same bid, the average would be this bid, putting both teams at their indifference points. In this special case, a coin toss, but without a winner and a loser, could be used to determine which team is offence and which is defence — for example, heads A is offence, tails B is offence. This outcome is still fair by our definition, except the equal advantage that each team enjoys over its indifference point is zero.
It pays to be honest
Can a team benefit by unilaterally deviating from its sincere indifference point and bidding insincerely? Suppose that A insincerely bids x, where 20 x 30, so it overbids. Then it does even better playing offence at the mean of the bids, which puts it closer to 30 than 20. But it will do worse if it underbids (x 20), so its optimal deviation is bounded from below. While A can benefit from overbidding — up to a point (30) — it will not know this, since it does not know that team B will bid 30. Indeed, because this is a game of incomplete information, A cannot even be sure whether it will underbid or overbid B.
Next suppose A bids x > 30. Then it will play defence and be worse off, because this will enable B to move the ball less than 70 yards to score. Not only does B do better than its indifference point, but A would much prefer to be in B's position, since 30+ is well above A's indifference point of 20.
Clearly, risk-averse, and perhaps even risk-neutral, teams have an incentive to be sincere, because deviating in either direction — by any amount in one direction (for A, going lower), and by a larger amount in the other direction (for A, going higher by more than 10) — hurts. Hence, sincerity seems a compelling strategy in the bidding game.
Application of bidding to soccer

Philipp Lahm scores in the 2012 UEFA Champions League Final. In soccer a coin toss decides who takes the first kick in a penalty shootout. Image: Markus Unger.
Penalty kicks in soccer occur from the penalty mark, which is 11 metres from the goal line. They usually occur in knock-out soccer tournaments or cup competitions when the score is tied after regulation play and extra time.
The team to make the first kick is decided by a coin toss, after which the teams alternate until each team has attempted five kicks. If no team is ahead on goals after these five kicks, the teams proceed to the next stage, in which they alternately attempt a single penalty kick until one team is ahead on goals and declared the winner.
As in the NFL, there is an advantage to winning the coin toss: statistics indicate that the team to kick first wins in about 60% of the games, giving it a 3:2, or 50%, advantage over the second-kicking teams. But having each team bid on the distance from which it kicks, and awarding the high bidder the first kick at the mean of the two bids, is problematic because being too close to the goal (e.g. six or fewer metres away) is probably more of a disadvantage than an advantage. This is because the goal-keeper can more easily block a shot from such a short distance, even though he or she has less time to do so. Accordingly, while we propose that the team that bids the greater distance go first, the losing team would be required to kick from the standard 11 metres.
Would either team be motivated to bid exactly 11 metres? Clearly not, because it would have an incentive to bid one centimetre more and not materially affect its chance of scoring a goal. Consequently, the competition will be over which team bids a greater distance than 11 metres. What is less clear is how much greater than 11 metres will the bids of teams be in order to render themselves indifferent between going first and going second.
It seems evident that this calculation will depend on the quality of their, and their opponent's, kickers and goal-keepers. But whatever the calculation of each team, bidding will help to level the playing field and make the teams — not the luck of the draw — accountable for their choices.
Conclusions
Our proposal that teams bid on the starting yard line in the overtime period of football, or the distance from which to make penalty kicks in soccer, eliminates the chance element of tossing a coin. This renders each team more satisfied with its choice, and by the same amount, than the other team's choice.
Bidding will inject a new element of strategy into each sport, which will create suspense about which team becomes offence and defence, and from where, in football, and which team kicks first in soccer, and from what distance. Although football and soccer fans may argue that bidding is not a "pure" test of competition, neither is tossing a coin. Among other advantages, bidding makes the teams responsible for their choices rather than allowing them to blame their poor performance on bad luck.
Sports are continually evolving to become fairer. Witness the National Basketball Association's (NBA's) institution of the three-point line in 1979 to reward the extra skill needed to make a longer shot, and the NFL's adoption of the two-point conversion in 1994 to double the reward from running or throwing rather than kicking for extra points. In soccer the introduction of penalty cards in 1970 to make referee decisions clearer to players and coaches, and the introduction of goal-line technology in 2012 to determine if a ball passes the plane of the goals, are examples of innovations in this sport. We believe that the evolution of overtime rules in both football and soccer should be no different.
About the authors
Steven Brams is professor of politics at New York University. He is the author most recently of Mathematics and democracy: Designing better voting and fair-division procedures (Princeton University Press, 2008) and Game theory and the humanities (MIT Press, 2011), as well as several Plus articles on game theory, fair division and voting. Zeve Sanderson is an undergraduate, majoring in politics, at New York University.
Comments
Anonymous
I really like this, the XFL should have thought about things like this before, well. Nevermind.
One way to make the NFL section clearly would be to phrase it in terms of "yards to go". So for your example the numbers would be 80, 70, etc. This is much more natural and useful as the yardage units on a football field are hilariously stupid [it should either count from 0->100 or from 50->0->50] you can just skip to the punch line: "How far does my offense have to go?" or "How many opportunities will my defense have to get a stop?" It'll make the comparisons easier especially since, in theory, a team could bid a total distance of less than fifty yards if they're all defense and no offense.
Anonymous
a lot of the concepts mentioned do not apply to a zero-sum game
Anonymous
How about a full auction in which the teams alternate bids, each one (a positive integer) less than the previous bid, until one team concedes, and the winning bid gets the ball on their own N yard line where N is the winning bid. Coin flip for who gets first bid. Less complex strategy involved this way which is good, but the averaging approach takes into account the different valuations that different teams would place on being on offense or defense.
The practical reality is that no bidding system would ever be used-- too complicated. What might work is an agreement that starting at, say, the 12 yard line, or whatever yard line is neutral with respect to who will (on average over all games and teams) score first -- to be computed by looking at past data and fixed once and for all for every game. Then flip a coin to in which the winner decides whether to start on offense or defense. Quick and easy, if not as interesting as the bidding methods.
Anonymous
The comments on the NFL make sense and are intriguing. They make it a fairer way to decide who takes the ball without altering the rules of the game, in that in NFL a team will at different times take the ball from different positions.
In football penalties are taken from the penalty spot. It isn't an option to take them from different places. That isn't making an arbitrary system fairer, it is fully altering the game. In general though the team winning the coin toss doesn't decide to go first, they decide to take the penalties at the end of the field nearer their most vocal fans. The team losing is then left to decide to go first or second.
Anonymous
According to the FIFA Laws of the Game, the referee is the one who decides which end to play the kicks towards. This is announced to the players before the coin is flipped. In other words, the coin toss only determines who goes first. If he is letting direction be a coin toss option for the winner, then he doesn't know the rules. And if the game is important enough to have kicks from the penalty mark, then a referee that doesn't know the rules shouldn't be working it.
Strphen Roe
This will never work in real NFL life, as both teams will ALWAYS bid ZERO, as possessing the ball first is vastly more important than whether you start on the 30 yard line, the 25, the 20 or even the 10. That point has been conclusively established by actual play - see results of coin toss in determining the winner, that initial possession is the MOST DETERMINATIVE FACTOR!