
Understanding turbulence
Aircraft turbulence is just one of the phenomena that Fluid Dynamics seeks to explain. By solving suitable equations, mathematicians can create computer simulations of observed cases of turbulence.

Here is an example. The computer model starts with a thin horizontal layer of air. Above and below the layer, the wind is blowing at different speeds.
A side-on view of the horizontal layer of air before turbulence forms.

A vertical slice through an atmospheric layer becoming turbulent.
An aeroplane is shown to give some idea of scale.
As a result of the difference in wind speed and direction across the layer, the fluid in the layer may do a series of 'somersaults', wrapping itself into a row of spirals like Swiss rolls. The view is from above and to one side, and shows only what happens to a single vertical slice through the row of spirals. The wrapping-up process brings heavier air over lighter air, the two tending to intermingle as the heavier air tries to move downwards and the light air upwards. The result is the turbulence you feel on board an aircraft. The spirals may be ten or more times the size of a jumbo jet (shown near the middle of the picture).

Turbulence in the laboratory: the tilting tank experiment.
Laboratory experiments can also show turbulence. In the tilting tank experiment, the scale of the turbulence is minuscule compared to the scale of turbulence that affects aircraft, but the phenomenon is essentially the same. Computer simulations can predict the experimental observations remarkably well.
Where is the mathematics in this? Of course, the computer program that does the simulation has to be based on a mathematical model of air or water.
Fluid dynamics - a science of immense practical importance
Air is just one example of a fluid: water another example. The study of the way fluids behave is known as Fluid Dynamics. It is a science of immense practical importance (for instance it includes aerodynamics, the science of how aeroplanes stay up). This is a highly mathematical discipline and a great deal of research into fluid dynamics is done in university mathematics departments, as well as in engineering departments.
Mathematicians use vector fields to describe the motion of fluids. Vector means something that has magnitude and direction. The velocity of air is an example of a vector: it has magnitude (speed) and direction. The velocity of air may also vary from point to point in space: this is an example of a vector field. The velocity of the air may also vary with time. Both the space and time variation may be shown in the notation as, for instance,u ( x, t )
where u is the velocity, x is the position in space, and t is time.
Newton's Law of Gravitation explains the motion of the planets around the sun
The branch of mathematics on which all this is based is called vector calculus.Calculus is about the way things vary, and vector calculus is about the way vector fields vary (both in space and in time). Calculus was discovered in the 17th Century principally by Isaac Newton in England and Gottfried Leibnitz in Germany.
At first, the calculus was applied to the study of particle-like bodies in motion. Newton's greatest triumph was to use the calculus to build a mathematical model of the solar system that was simple, yet extremely accurate. He showed that simple laws of motion and a simple law of gravitation accurately explain the motion of the planets around the sun. For this purpose, the planets do behave almost exactly like particles, one reason being that their sizes are very small in comparison with their distances from the sun.
A fluid like air or water is made up of lots of tiny particles, called molecules. You can think of each particle as pushing on its neighbours. In a gas like air, the particles hit each other and bounce off; in a liquid like water, there is a continual jostling, like people trying to get into a football ground. Each particle obeys Newton's laws of motion — the same laws that explain the motion of the planets! But instead of simple planetary motion, you get a rich variety of fluid behaviour, as you can see for yourself every time you stir milk into coffee. To make a mathematical model of fluid motion, it is necessary to use the calculus.
Water squirts under pressure!
What is pressure? It is a measure of how hard the fluid particles are pushing their neighbours, on average. Archimedes of Syracuse (ca. 287-212 BC) may have been the first to understand pressure in a scientific way. But he studied it only for fluids at rest. This is called "hydrostatics". Archimedes was a great genius, but he had no way of knowing about the calculus. So he did not know how to extend his ideas to fluids in motion.
Even after the discovery of the calculus, it took many years before anyone saw how to extend Archimedes' ideas. Nobody could explain, with any precision, even commonplace observations of fluids in motion such as the way water squirts under pressure. It was the mathematician Daniel Bernoulli (1700-1782) who took the next step, by discovering the famous Bernoulli equation. He derived it by combining Newton's laws of motion with Archimedes' idea of pressure, using the calculus. (See "Daniel Bernoulli and the making of the fluid equation".)
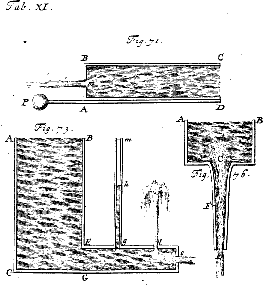
Illustrations from Daniel Bernoulli's book Hydrodynamica.
Source: The Turner Collection, Keele University.
The Bernoulli equation explains squirting. It explains how birds and aeroplanes stay airborne. It explains why, if you pick up a sheet of paper by one edge, then blow on it, the paper moves upwards rather than downwards. Try it!
The Bernoulli equation is usually written like this:
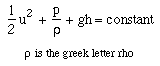
As before, the symbol u stands for the fluid velocity. The other symbols, in order, stand for the pressure, p, the density, rho (the Greek letter in the denominator), the acceleration due to gravity, g , and the height, h , of the particle above some given reference level such as sea level. (The value of g on our planet is about 10 metres per second per second.) For the Bernoulli equation to apply accurately, the flow must be frictionless and steady. Steadiness simply means that the velocity field — considered as a vector field — does not change with time: u(x,t) = u(x). Real fluid flows are never exactly frictionless, nor exactly steady, but the Bernoulli equation may still be a useful approximation.
The equation applies only along a single path followed by a particle of fluid. In steady flow, such a path is called a streamline. At any point on the streamline, you can add up the three quantities on the left of the Bernoulli equation. The equation says that if you do that for any two points on the same streamline, then the two answers will be the same.
In particular, if the fluid is moving horizontally, then — contrary to what you might guess — the pressure p will be lower where the fluid is moving faster. This certainly surprised many of Bernoulli's contemporaries, and it still surprises people today. But it explains, for instance, how squirting works. You fill a balloon with water and squeeze it. The pressure p is high inside, and low outside. The water is moving slowly inside, and fast outside. The equation really does make sense!

The water pressure is lower where the water is moving faster.
If you squirt horizontally, the jet of water will curve over and fall under gravity. It will go faster and faster as it falls, even though p now has to stay close to atmospheric pressure. The term gh in the Bernoulli equation is now decreasing, and u must increase to compensate. So that makes sense too.
Aeroplane wings generate lift
The Bernoulli equation explains how an aeroplane wing can generate lift. The experiment on the sheet of paper is a similar case. The flow over the wing has streamlines like this:
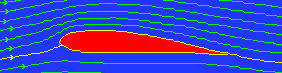
Cross section of an aeroplane wing. Air streamlines passing a wing
Imagine that the wing is stationary and the air flowing past it from left to right. Consider streamlines far ahead of the wing, where the pressure and air velocity are much the same across the streamlines. Consider two streamlines which are very close together ahead of the wing, whose paths divide with one going close to the upper wing surface and one going close to the lower wing surface. As the diagram shows, the streamlines crowd together above the wing, which shows that the air speed is higher there than below. Bernoulli's equation predicts that the higher air speed implies lower pressure. Therefore pressure is higher on the lower surface than on the upper surface, and this explains lift.
Modern advances in the mathematical study of fluids enable more efficient wings to be designed. It is reported that a computer simulation has shown how the wing of a jumbo jet could be redesigned to reduce drag by over 20%, by using the most powerful supercomputers and being extremely clever with the mathematics. New aeroplanes designed this way will save fuel worth millions of pounds per year.
Mathematics describes fluid motion
Bernoulli's work and that of his contemporaries had many limitations, including the limitation to steady, frictionless flow. The limitation to steady flow was removed by Leonhard Euler (1707-83). It was not until the 19th century that the limitation to frictionless flow was removed, through the efforts of several mathematicians including Augustin Louis Cauchy (1789-1857) and George Gabriel Stokes (1819-1903). The equation that resulted is more complicated than Bernoulli's; it uses vector calculus. It is usually written like this:
Here, if you are not familiar with the notation, think of the left hand side as the acceleration of a fluid particle. Think of the del as a mathematical operation that relates to the way velocity and pressure change from point to point in the fluid at any one time. n (pronounced nu) is the coefficient of viscosity.
Although this equation was discovered well over a century ago, its predictions and consequences are far from being completely understood today. The study of the equation has given rise to a whole branch of high-powered mathematics on its own, as well as to some of the toughest demands on supercomputer power (as with the design of efficient aircraft wings -- to say nothing of weather forecasting). Most intriguing of all, the weight of evidence says that, as far as we can tell, this simple-looking equation describes quite accurately the intricate complexities of turbulent flow. Scientists often call this equation the "Navier-Stokes equation" of fluid motion. It can be generalized to describe many other phenomena, such as the behaviour of the hot plasma in the interior of stars, and even the way that inter-stellar and inter-galactic gas behaves.
It is the Navier-Stokes equation which lies at the foundations of modern fluid dynamics.

Mosaic of 45 images taken between Jan. 1994 and March 1995 of M42, the Orion Nebula.
source: NASA.
Set up your own demonstration of turbulence
Next time you run a bath you can set up your own demonstration of turbulence. Add a few drops of coloured bath essence in a line across the bath. Hold your hand flat with the fingers together and swish it through the water across the line of coloured water. You should see swirls form at each edge of your palm as it moves.
When can I study Fluid Dynamics?
Fluid Dynamics is included in many mathematics and engineering degree courses. The topic is usually introduced in the second or third year of the course. The study of fluids requires mathematical techniques (such as vector calculus) which are usually taught early in such degree courses.
The editorial team would like to thank Prof. M.E. McIntyre, Dr J.F. Scinocca of the Atmospheric Dynamics Group, and Dr S. Dalziel of the Fluid Dynamics Laboratory, Department of Applied Mathematics and Theoretical Physics in Cambridge for their help in producing this article.
In our next issue: a simple experiment for testing Bernoulli's equation that you can do yourself.