Outer space: Rugby and Relativity
When most of us have an encounter with the relativity of motion it is with Galileo's sort of relativity rather than Einstein's. Who has not had the experience of sitting in a stationary railway carriage at a station, and suddenly sensing that we are in motion, only to recognise that a train on the parallel track has just moved off in the other direction and we are not moving at all?
Here is another example. Recently, I spent two weeks visiting the University of New South Wales in Sydney during the early stages of the Rugby World Cup, which was dominating the media and public interest. Watching several of these games on television I noticed an interesting problem of relativity that was unnoticed by the celebrities in the studio: What is a forward pass relative to? The written rules are clear: a forward pass occurs when the ball is thrown towards the opposing goal line. But when the players are moving the situation becomes more subtle for an observer to judge, due to relativity of motion.
Imagine that two attacking players are running in parallel straight lines 5 metres apart at a speed of 8 metres per second towards their opponents' line. One player, the "receiver", is a metre behind the other, the "passer", who has the ball. The passer throws the ball at 10 metres per second towards the receiver and is stopped by the defenders. The speed of the ball relative to the ground is actually (102+82)1/2=12.8 metres per second and it takes 0.4 seconds to travel the 5 metres between the players.
During this interval the receiver has run a further distance of
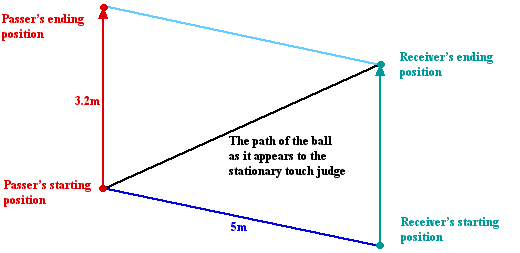
The judge believes that there has been a forward pass and waves his flag, but the referee is running alongside the play, doesn't see the ball go forwards, and so waves play on!
Can you think of any other sports where relativity might be an issue?
Did you manage to answer the puzzle posed in Outer space: Independence Day? If not, you can find the answer here!
Comments
Anonymous
In what sense is the ball moving at 10 meters per second? "The speed of the ball relative to the ground is actually (10^2+8^2)1/2=12.8 metres per second," and if "it takes 0.4 seconds to travel the 5 metres between the players," then relative to the players the speed is 12.5 meters per second (5/0.4). Also, if the time it takes the ball to reach the other player is 0.4 seconds than its speed relative to the ground is (√(5^2 + (0.4(8))^2))/0.4 = 14.84. However, if it takes the ball 0.5 seconds to reach the other player than its speed relative to the players is 5/0.5 = 10 meters per second, and its speed relative to the ground is (√(5^2 + (0.5(8))^2))/0.5 = 12.8.