"My boomerang won't come back" goes the song about the disgraced Australian Aborigine.

Well, that's not so bad a thing because boomerangs used for hunting kangaroos aren't meant to come back - they are heavy, hockey-stick-shaped throwing sticks that move in a confusingly wobbly path, and they are designed to break the legs or wings of any 'roo or bird they encounter. So just imagine if that 'rang came back: how would you catch it? It would be as silly as if Robin Hood's deadly arrows came back! The only boomerangs that do come back are those intended to be used as toys and for sport: the Aborigines knew about the fun you can have with boomerangs thousands of years ago.

Figure 1: Traditional boomerangs from Australia.

Perhaps surprisingly, it's reported that the earliest known users of boomerangs were found in what is now Poland, about twenty thousand years ago (18,000 years BC!). Their boomerangs were the traditional bent-stick variety, like the Australian boomerangs in figure 1.

It wasn't too hard for boomerangs to be discovered by accident because if you were stuck for food you might try throwing a rock, a stick, anything at your prey, and if the stick you found did funny things you might think it was a magic stick and you'd want to keep it for another throw.

Figure 2: Some modern sports boomerangs.

These days, we can make boomerangs in many other curious shapes (figure 2), and some of them fly much better than the traditional ones.

In fact, a cross-shaped balsa-wood "boomerang" that looks like a 4-bladed propellor (figure 3) works really well indoors - inside the average-sized living room! We show you how to make one of these in our Bang up a Boomerang! article.

Figure 3: Home-made balsa wood boomerangs, suitable for indoor use.

Why do boomerangs fly?

This is the 64,000 Euro question. First let me ask 10 fairly simple (but increasingly complicated!) related questions. If you can answer all of them, then you're well on the way to understanding how a boomerang works:

1. What is (near enough) the shape of the flight path of a boomerang?

A. out and back on a straight line;

B. circular;

C. around the four sides of a square.

2. If I swing a ball on string around my head it follows a circular path; in what direction does the force in the string act?

A. downwards;

B. always towards the centre of the circle;

C. there is no force in the string.

3. An aeroplane wing works because:

A. it is an anti-gravity device;

B. when it moves through the air at high speed it generates lift;

C. it flaps up and down.

4. A helicopter rotor has four blades each in the shape of:

A. a feather;

B. an airplane wing;

C. a circular tube.

5. A cross-shaped boomerang resembles a helicopter rotor because:

A. they both have four blades;

B. they both generate lift when they spin;

C. they work backwards as well as forwards.

6. The lift force of a spinning boomerang is directed mostly:

A. downwards;

B. towards the centre of its circular flight path;

C. there is no lift force.

7. As a spinning boomerang moves forward the uppermost blade moves:

A. at the same speed as the centre of the boomerang;

B. faster than the centre of the boomerang because it is spinning and moving forwards at the same time;

C. downwards.

8. The top of the boomerang generates more lift than the bottom because:

A. it is bigger;

B. it is moving faster;

C. it is heavier.

9. The difference in lift between the top and the bottom of the boomerang:

A. doesn't matter;

B. forms a couple which causes gyroscopic precession;

C. causes the boomerang to bend.

10. Lift on a boomerang causes circular motion and gyroscopic precession:

A. which is too complicated for me to understand;

B. which balance perfectly - truly a wonderful miracle of nature;

C. which the Aborigines could have told you 10,000 years ago.

Well, as you might have guessed, the correct answer to all the questions is B. So you have got the idea now that a boomerang works because it spins as it moves forward and the bit of the boomerang that is at the very top moves forward faster than the bit at the bottom so it generates more lift.

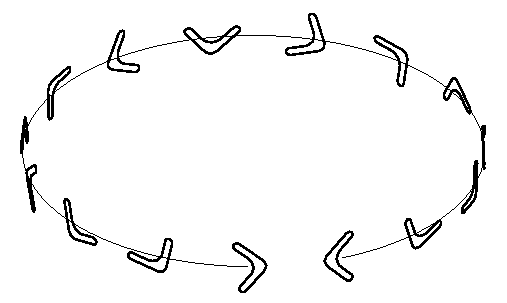
Figure 4: Flight path of a boomerang.

The overall lift force (like a spinning propellor) points towards the centre of the circular flight path which is necessary for circular motion (centripetal acceleration and all that) but the boomerang has to turn to face forwards all the time as it goes around the circle (figure 4 shows the flight path of a boomerang). This is achieved by the difference in lift force between top and bottom . This difference creates a couple, and this couple causes precession. Let's look at this in more detail.

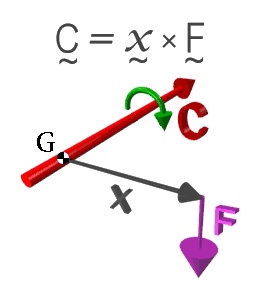
Figure 5: A force at a distance producing a couple.

What is a couple?

A couple is just an "angular force". We all know that to make a roundabout rotate, it is easiest to push on it as far away from the centre of the roundabout as possible. Our pushing is turned into an "angular force" which turns the roundabout; and the pushing is more effective the greater the distance between where we apply the force and the pivot.

A couple therefore has two aspects: a force, and a distance between the line of force and the point of rotation. The magnitude of the couple is given by the product of this distance and the size of the force, and the direction of the couple is at right angles to both. In Figure 5, the couple C is represented by the red arrow, the point of rotation is the little black and white circle marked with a G, and the black arrow x is the position vector of the point where the force is applied. The definition of a couple is most succinctly expressed as C = x x F.

Any solid body also has an "angular mass", which is properly called the moment of inertia of the body. It takes account of how far away the mass is from the centre of the body: mass which is further away from the point of rotation takes more "angular force" to rotate. For example, a roundabout with all the children right at the edge is more difficult to turn than one where all the children are clustered in the middle! Gyroscope designers put as much mass as they can into the rim of the gyroscope to give them really big moments of inertia.

The physics of boomerangs

A boomerang does funny things because it is in fact a gyroscope. Aerodynamic forces generate a twisting moment which cause the "gyroscope" to precess and to move on a circular path.

You can read all about gyroscopes and the physics behind them in this issue's feature article, Galloping gyroscopes.

However, to understand what precession is, you simply need to observe that as well as spinning quickly round its own axis, the boomerang slowly changes the direction in which it is pointing (see the flight path illustration of figure 4). You can observe precession yourself if you get an old-fashioned spinning top (yes, they still make them!) and spin it on a smooth surface: as well as spinning about its own axis, a well-balanced top should circle around on the surface beneath it.

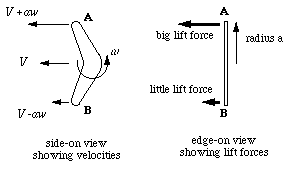
Now let's examine the forces acting on a boomerang of radius $a$. The centre of the boomerang is moving at a constant forward speed $V$ and the boomerang is spinning with angular velocity $\omega$, as shown in the diagram. The "top" end {\bf A} is therefore moving faster than $V$ with speed $V+a\omega$, and the "bottom" end {\bf B} is moving slower with speed $V-a\omega$. A wing generates more lift when it is moving faster so point {\bf A} is generating more lift than point {\bf B}.

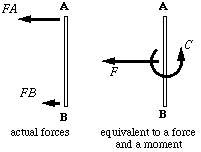
The two forces $F_A$ and $F_B$ can be represented by a single force $F$ and a single couple $C$. With this simple representation of the forces acting on the boomerang we can give two reasons why it moves on a circular path:

1. A constant centripetal force $F$ produces circular motion with velocity $V$ on a radius $R$ such that \par \begin{equation} F = mV^2/R \end{equation} where $m$ is the mass of the boomerang.
2. A constant couple $C$ acting on a gyroscope spinning at angular velocity $\omega$ causes steady precession at rate $\Omega$ such that \begin{equation} C = J\omega\Omega \end{equation} where $m$ is the mass of the boomerang and $J$ is its moment of inertia.

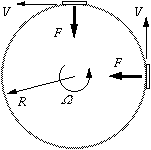
\setcounter{equation}{2} If the rate of precession $\Omega$ exactly corresponds to the angular velocity of circular motion, then the boomerang rotates at exactly the correct rate to stay tangential to the flight path as shown. This gives an equation relating $V$ to $\Omega$, \begin{equation} V = R\Omega \end{equation} A wing of area $A$ moving at speed $v$ in air with density $\rho$ generates an aerodynamic lift force $L$. It can be shown that $L$ is proportional to the air density, the wing area and the square of the wing speed. The precise relationship is expressed using the proportionality constant $C_L$, which is known as the lift coefficient, and takes the following form: \begin{equation} L = \frac{1}{2}\rho v^2C_LA \end{equation} It can also be shown by integrating the lift force over the area of a cross-shaped boomerang that the net lift force $F$ and aerodynamic couple $C$ are given by \begin{equation} F = \frac{1}{4}\rho(V^2+(a\omega)^2)C_LA_s \end{equation} and \begin{equation} C = \frac{1}{4}\rho Va^2\omega C_LA_s \end{equation} where $V$, $\omega$ and $a$ are the velocity, spin speed and radius of the boomerang as before, and $A_s = \pi a^2$ (the swept area of the boomerang). \par From equations 2, 3 and 6, we find that the radius $R$ of the circular flight path is independent of spin speed $\omega$ and forward velocity $V$, and that it is a constant for a given boomerang: \begin{equation} R = \frac{4J}{\rho C_L\pi a^4} \end{equation} For the case of a cross-shaped boomerang, $J = \frac{1}{3}ma^2$, and equations 1, 5 and 7 can be arranged to give \begin{equation} a\omega = \sqrt{2}V \end{equation} which defines the "flick-of-the-wrist" needed to make the boomerang fly properly.

About the author

Hugh Hunt showing how a real Aussie throws a boomerang (mind those windows, Hugh!)

Dr. Hugh Hunt is a Lecturer in the Department of Engineering at Cambridge University, and a Fellow of Trinity College, where this photo was taken.

He hails from Melbourne and has an impressive collection of boomerangs, including one salvaged from somebody's kindling pile! You can find out more about boomerangs on his website.