How hard is the Rubik's cube?

Submitted by mf344 on July 4, 2011

A Rubik's cube, you'll be pleased to hear, can always be solved in at most 20 moves, no matter how badly it was scrambled up to start with. Mathematicians have proved that that's true, and they've also proved that 20 is the best you can do: there are particularly horrible starting positions for which you do need 20 moves. (A move is any twist of any little face.)

Twenty is the Rubik's cube god's number, so-called for the following reason. Any constructive approach to solving a Rubik's cube requires some sort of method, or algorithm. For example, you might try to solve one side first, then another, and so on. An algorithm that solves the cube in the smallest possible number of moves for any given starting position is called god's algorithm: even if you can't figure out what that algorithm is, god, being omniscient, certainly can. The number of moves that god's algorithm takes from the worst possible starting position is god's number.

A bigger cube

So far, so good, but what if you're looking at a bigger cube, one that has four little cubes in each row, or five, or six, or even more? What's god's number then? That's an incredibly hard question. Even for the standard $3 \times 3 \times 3$ cube there are 43,252,003,274,489,856,000 starting positions of the cube. To work out god's number for the standard cube researchers cleverly exploited the symmetries involved to figure out how to solve it from all these positions, but they still needed the equivalent of 35 years' of computing time on a single computer to crack the problem. A similar approach for bigger cubes would require computing power that goes far beyond what's available today.

However, a group of researchers from MIT, the University of Waterloo and Tufts University have managed to come up with an approximate answer. They have shown that for large enough numbers $n$ , god’s number for an $n \times n \times n$ cube is proportional to $n^2/\log {n}.$ This means that you can find two positive numbers $c_1$ and $c_2$ , and a third positive number $N$ so that for all $n>N$ , god’s number $g(n)$ satisfies

$c_1 \frac{n^2}{\log {n}} \leq g(n) \leq c_2 \frac{n^2}{\log {n}}.$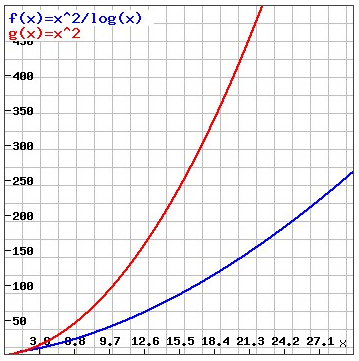

The blue curve is the graph of n²/log(n) and the red curve is the graph of n².

This may seem woefully imprecise, but it gives you a rough idea of the rate at which god's number increases as the cube gets bigger. Computer scientists like these kind of results, because they measure how quickly a problem becomes harder as it gets bigger in size and so give them an idea of the chance a computer has of solving ever-harder levels of the problem in a reasonable amount of time.

Researchers had already known that god’s number for the Rubik’s cube is proportional to $n^2$ . An $n \times n \times n$ cube has $6n^2$ little faces: there are 6 faces of the big cube each of which contains $n^2$ little ones. Solving the cube means manoevering each of these little faces into the right position. It’s possible to show that the cube can be solved in a constant number of moves for each little face, which means that the number of moves needed is proportional to $6n^2$ . And since you can ignore constant factors in results about proportionality, this means that god’s number is proportional to $n^2$ .

What’s new about the result is the fact that the researchers were able to reduce $n^2$ by a factor of $1/\log {n}$ . They did this by cleverly exploiting the fact that a sequence of moves can put several little faces into the right position at the same time. The researchers actually give an explicit algorithm for solving a scrambled cube making use of this fact.

So next time you find yourself confronted with a large and scrambled Rubik's cube, have a look at their paper.