
The world around us is full of relationships, rhythms, correlations, patterns. And mathematics underlies all of these, and can be used to predict future outcomes. Our brains have evolved to survive in this world: to analyse the information it receives through our senses and spot patterns in the complexity around us. In fact, it's thought that the mathematical structure embedded in the rhythm and melody of music is what our brains latch on to, and that this is why we enjoy listening to it. It is perhaps not surprising then that there is a great deal of overlap between mathematics and the art that our brain finds so pleasing to look at.
This article is a whistle-stop tour of some of the types of art with a strong mathematical component, or conversely where a mathematical visualisation has an astonishing beauty.
Geometric patterns

The "Flower of Life" pattern
Mosques throughout the world are decorated with extremely elaborate geometrical patterns of simple shapes. This is because Islamic art (in contrast to that of other faiths, with their murals, paintings and stained glass windows) traditionally avoids the depiction of people and animals, and instead involves repeating geometric patterns. These regular arrangements are said to symbolise the divine order of the Universe. However, the artist often includes a deliberate mistake in acknowledgement of the belief that only Allah is truly perfect.
The Golden Ratio
The ancient Greeks did some of the finest maths in history - we owe much of our understanding to them. One of the numbers that particularly interested them is known as the {\it Golden Ratio}. A rectangle constructed with sides in proportion to the ratio of 1 to 1.618 to 3 decimal places (to be precise,
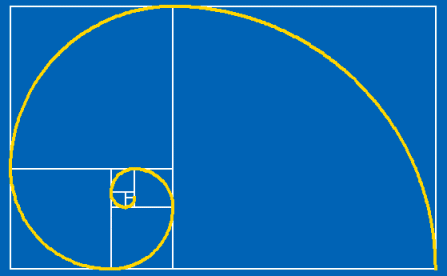
The Golden Curve
The value 1.618 is itself very curious. It was discovered by the Greeks as the positive solution to the basic quadratic equation x2 - x - 1 = 0. The ratio of successive terms of the Fibonacci sequence, where each new term is the sum of the two previous (i.e. 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,...), also tends towards this value of 1.618.... This series turns up throughout nature, from the number of petals in a flower, to the pattern of seeds in Sunflowers to the swirl in a Nautilus shell.
The Greeks appreciated the special nature of the Golden Ratio, and thought that objects in this proportion were particularly pleasing to the eye. It is said that they used it to ensure the beauty of statues and architecture, for example in the dimensions of the Parthenon. This practice was apparently passed down through history, so that even the figures in Leonardo Da Vinci's paintings, or Michaelangelo's David are proportioned according to this ratio. You can find out more about the use of the Golden Ratio in art in The golden ratio and aesthetics from a previous issue of Plus.
However, although there is strong support for the presence of this Fibonacci "Golden" ratio in nature, whether Ancient or Renaissance artists really did use it in their work or whether it is only a numerological coincidence is much more contentious. In fact, recent psychological experiments have failed even to show that people have any preference for this proportion, compared to either "thinner" or "squatter" rectangles. There is a very interesting article by Keith Devlin on the facts and fictions of the Golden Ratio in art on the website of the Mathematical Association of America.
Geometric abstractionism
Piet Mondrian was one of the founding members in 1917 of a Dutch art movement called De Stijl (meaning "The Style") or neo-Plasticism. Mondrian's style of painting involved the use of strictly horizontal or vertical black lines to create a grid of rectangles, some of which were filled in with black or white, or vivid red, blue or yellow. You can see an example of Mondrian's work at the website of the Museum of Modern Art in New York.
Mondrian believed that, despite their complexity and variability, natural scenes are composed of basic components and regularity. So he tried to create faithful reproductions by painting only these fundamentals and their relationship with each other, using only the prime colours and elements of geometric mathematics - straight lines, right angles and quadrangles - to create his reflection of reality.
Abstract paintings from graphs

Crossing at the Left Border, by Margaret Leiteritz
Tessellations
![[IMAGE: Regular division of the plane]](/issue33/features/dartnell_art/flat.jpg)
M.C. Escher's "Regular division of the plane".
All M.C. Escher works © 2002 Cordon Art - Baarn - Holland (www.mcescher.com).
All rights reserved. Used by permission.
Origami

Origami is the Japanese craft of creating wonderful three-dimensional shapes and models solely by folding paper - usually a single square sheet (ori meaning folded and kami meaning paper). The links between this ancient art and mathematics are profound. If you unfold a finished model you will see a complex geometrical pattern of creases made up of triangles and squares, many of which will be congruent (because they were produced by the same fold). The construction step known as a "push fold" is mathematically equivalent to bisecting an angle.

The regular polyhedra. Image used by permission of Polycell
Maths classrooms are often decorated with models of the nine "regular polyhedra". These are the three-dimensional solids that have every face the same. Five of them are convex, that is, the straight line joining any two points lies entirely inside the solid. These are often known as the Platonic solids: the tetrahedron, cube, octahedron, dodecahedron and icosahedron. The other four were not known to the Greeks, and are sometimes known as the stellated (starlike) regular polyhedra. The classroom models are usually made from card with scissors and glue, but they can also be made by origami. In fact, mathematicians have been able to prove not only that any polyhedron can be constructed by origami, but also that any outline drawn with straight lines (such as a star symbol *, or arrow →) can be cut out from a sheet of paper using a single scissor cut, once the sheet has been folded in the appropriate way.
Anamorphic Art

The Ambassadors (1533), Holbein
"Anamorphis" is a form of art that was first experimented with during the Renaissance and became particularly popular during the Victorian era. It involves distorting an image so that it is unrecognisable unless viewed in the right way. For example, Hans Holbein's The Ambassadors (1533), at the National Gallery in London, contains a skull (symbolising the transience of life) that has been grossly stretched. It only becomes recognisable when viewed from a very oblique angle, by standing practically alongside the left-hand edge of the painting.

Fractals
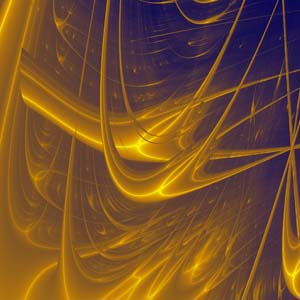
A detail from the "Lyapunov Exponent"
by Andy Burbanks
When the sensitivity of a complex system to small changes is mapped on the plane, the result is often a fractal. When this map is colour-coded, the result can be strikingly beautiful. The "Lyapunov Exponent" fractal on the left is one example, and you can find out more, and see some more beautiful images, in Extracting beauty from chaos from issue 9 of Plus.
Minimal energy surfaces

Minimisation problems can also be solved in three dimensions. The spherical shape of a soap bubble is due to all the molecules in the surface attracting each other and pulling the thin film into the smallest possible area. A raindrop on a leaf is under further constraints and the resultant "minimal energy surface" is distorted into a flattened droplet shape.
Image by Ken Brakke

Antipot, by Bathsheba Grossman
This article can give only a brief glimpse of the enormous region of overlap between mathematical patterns and processes, and the world of art and aesthetics. A web search reveals many more examples, and it would be well worth keeping your maths hat on when you visit a gallery....
About this article

Lewis Dartnell read Biological Sciences at Queen's College, Oxford. He is in his second year of a four-year combined MRes-PhD program in Modelling Biological Complexity at University College London's Centre for multidisciplinary science, CoMPLEX. In 2003 he came second in the THES/OUP science writing competition, and in 2004 he came second in the Daily Telegraph/BASF Young Science Writer Awards. You can read more of Lewis's work at www.ucl.ac.uk/~ucbplrd.
Comments
very well done.
this is a very informative and comprehensive article.
Very helpful!
Thanks for this! It has helped me a lot with preparing an interesting art project for my students!
gr8 article...........enjoyed
gr8 article...........enjoyed reading it
What a help : )
Really useful for a forth coming project with Year 9's
zhézhǐ paper folding
In China, traditional funerals include burning folded paper, most often representations of gold nuggets (yuanbao). It is not known when this practice started, but it seems to have become popular during the Sung Dynasty (905–1125 CE).[2] The paper folding has typically been of objects like dishes, hats or boats rather than animals or flowers.[3]
Thanks a lot :) Helped me
Thanks a lot :) Helped me with my school project
There seem to be some errors
There seem to be some errors with your links you are pointing in your article to as an example, the only one that seemed to work is this link: http://plus.maths.org/content/os/issue9/features/lyapunov/index
Great wright up by the way, using it in next week class!
Thanks,
Sarah
Thanks for pointing that out,
Thanks for pointing that out, we have updated the links.
Math and art
Math its a poem ... its wonderfull
math
math is the best thing i have ever studied in my life ....i love maths
Math and Art
It is not a poem it is shapes and for a human eye too many shapes will be counted as 1