
This article about complex numbers is a little advanced. See here for a basic introduction to complex numbers.
Every positive real number has two square roots, one being the negative of the other. It's easy to tell them apart by specifying whether you're looking at the positive or the negative square root. This means you can unambiguously define the square root function
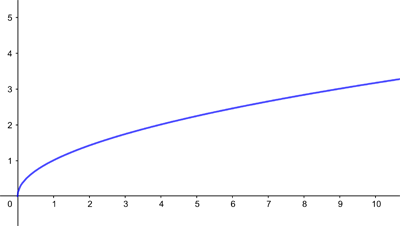
The graph of the positive square root function defined over the non-negative real numbers.
When it comes to the square root of complex numbers, things are a little tricker. Before we start, let's have a quick look at Euler's formula, which gives us a way of writing complex numbers that is convenient when it comes to taking square roots (see this article for more detail on Euler's formula).
Euler's formula
First remember that a complex number
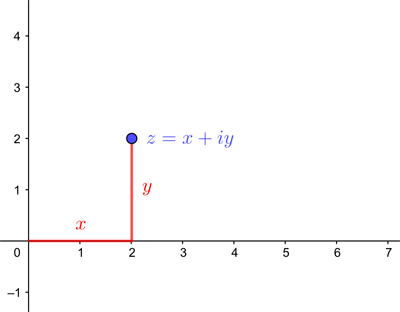
A complex number represented as a point on the plane in Cartesian coordinates.
Euler's formula tells us that
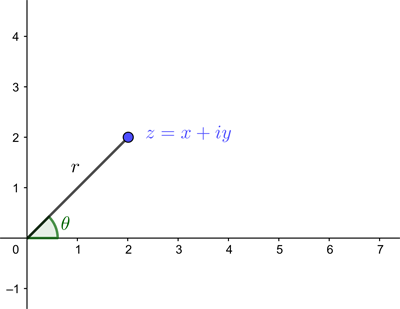
A complex number represented as a point on the plane in polar coordinates.
See see this article to find out why this is true.
This is the representation of complex numbers we will use in this article. The reason is that taking a square root of a number involves raising that number to the power
You can convince yourself that this is true by noting that the point with polar coordinates
The second thing to note is that we can also say what we mean by
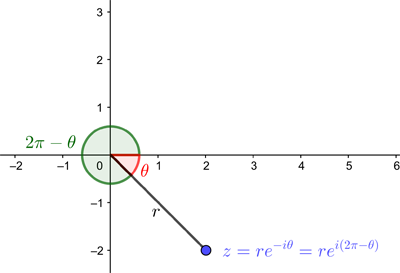
A negative angle can be interpreted as an angle measured in the clockwise direction from the positive x-axis.
Taking the square root
When it comes to the square root of a complex number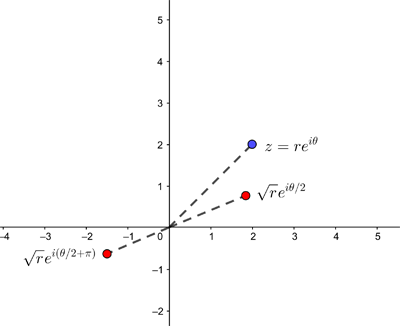
The two square roots (shown in red) for z (shown in blue).
Our two expressions,
Defining a function
Let's start by defining our square root function
Why can't we define our function on the whole plane in the same way?
Well, consider what happens as you approach a point on the negative real line from above and from below. We can approach the point from above by looking at points
A new surface
There is, however, a clever trick that gets us around this problem. The idea is to create a new surface on which it is possible to define a function for the complex square root in a continuous way. We start by taking two copies of the complex plane and cutting each along the negative real axis (such a cut is called a branch cut). On one copy of this cut complex plane we defineNow we glue the top edge of the cut of the first copy to the bottom edge of the cut of the second copy, and vice versa (this is hard to imagine but hang in there). On the resulting surface (called a Riemann surface) the square root function is now defined unambiguously and continuously.
To illustrate this, look at points
This is an illustration of the Riemann surface that comes from the cutting and gluing:
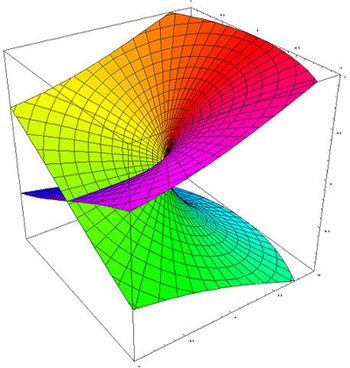
The Riemann surface associated to the complex square root, represented in three dimensions. A loop around the point 0 on this surface (which is right at the centre) will take you once around the top sheet and once around the bottom sheet. Figure: Jan Homann.
When you try to create this surface in three dimensions you run into problems: once you have glued the top edge of the cut of one copy of the plane to the bottom edge of the cut of the other copy of the plane, the two remaining free edges of the cut end up on different sides of the surface you have created so far. So the only way to glue those free edges together is to allow the surface to pass through itself. This is why a three-dimensional representation of this Riemann surface, like the one above, intersects itself. To get a surface that doesn't self-intersect you need to move into the fourth dimension.
The complex square-root isn't the only multi-valued function. Another example is the complex logarithm, which actually has infinitely many values. In this case the associated Riemann surface is a beautiful infinite stair case (of which a finite section is shown below).
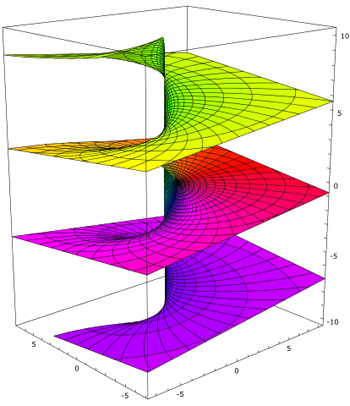
The Riemann surface associated to the complex logarithm. Figure: Leonid 2, CC BY-SA 3.0.
About this article
Marianne Freiberger is Editor of Plus.
This article is part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI), an international research centre and our neighbour here on the University of Cambridge's maths campus. INI attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.

Comments
Typo x = i y
Dear Marianne,
Thanx for a great article on complex square roots.
In the first sentence below “Euler's formula” you write
First remember that a complex number
the
Respectfully, Sabah
Thanks for pointing that out,
Thanks for pointing that out, we have fixed the typo!
Typo
There's a small typo in just after the title "Euler's Formula". You say that you can write z as x=iy but it must be x+iy.
Nothing serious but may affect the novices...
geogebra bug?
I like this article, but I think the geogebra applets are currently a bit buggy. In the first one, changing the r slider seems to change the real component of the blue point rather than its radius (if I set r=0 and theta=0.4 then I get a point on the imaginary axis, rather than the origin). In the second one, changing the r slider seems to have no effect on the red point.
Thanks for pointing out the
Thanks for pointing out the mistake, we have now fixed it.