
No limits for Usain
Usain Bolt, the "fastest man on the planet", aims to get his 100 metre world record of 9.58 seconds down to 9.40 seconds. What has mathematics to say about this quest?

Usain Bolt celebrates his victory over 100m and new world record at the Beijing Olympics. Image: Jmex60.
With his new goal, Bolt's average speed over the distance will have to be 10.64 metres per second or 23.80 miles per hour. He will actually have to hit even greater speeds because he leaves the blocks at zero speed and the first part of the race is spent accelerating to his peak velocity. Such a record as 9.40 would have been unthinkable pre-Bolt but people in the know are optimistic. Michael Johnson, an earlier world record phenomenon himself said "No-one can predict Usain Bolt's limits".
Whether Bolt is successful we shall have to wait and see, but the ambitious figure raises the question of whether there is an ultimate limit which no runner can possibly surpass. If there is one where would such a limit lie? For instance, is there a sub 9 second record in the offing?
There is no denying that world records are always being reduced. Sometimes this is done in a spectacular way, as with Bolt himself, or earlier by Bob Beamon in the 1968 Mexico Olympics long jump when he almost jumped out of the pit. More often records are shaved here and there, a few hundredths of a second off a sprint or centimetres off a jump.
Thinking mathematically the succession of world records in an athletic event give us a decreasing sequence of real numbers bounded below by 0. This is because even Usain Bolt, with all the superlatives heaped upon him, cannot run with infinite speed. Such a sequence must converge to a mathematical limit: a number below which our sequence does not venture, but to which it gets arbitrarily close. But this does not solve our problem because the appeal to a property of real numbers does not tell us where that mathematical limit is — and it may turn out to be 0 itself. In colloquial language this would mean that the world record has no limit at all.
There is no denying that records are improved and race times do appear to get closer and closer to a limit. But when it comes to matters of convergence, such rash conclusions can be dangerous. Just think of the harmonic series $$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+...$$ Although smaller and smaller bits are added at each step, the series goes on growing without any limit: it diverges.
Let's imagine a mythical world record for the hundred metres to be exactly 10 seconds in 1970. Furthermore we'll imagine that this record reduces by 0.1 of a second in the following decade, by a further 0.05 of a second in the decade after that, continuing by smaller amounts in later decades, the whole construction based on the harmonic series. Such reductions bear comparisons with the actual reductions in the official world record to date:
| Year | Actual world record | Actual reduction | "Harmonic world record" | "Harmonic reduction" |
| 1970 | 9.95 | 10.00 | ||
| 1980 | 9.95 | 0 | 9.90 | 0.1 |
| 1990 | 9.92 | 0.03 | 9.85 | 0.05 |
| 2000 | 9.79 | 0.13 | 9.817 | 0.033 |
| 2010 | 9.578 | 0.212 | 9.792 | 0.025 |
The progression of our mythical world record is slower than the progress of the actual world record, certainly from the year 1990 onwards. In the $kth$ decade after 1970 we are assuming the mythical harmonic world record is given by the expression $$10-\frac{1}{10}\left(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+ ... \frac{1}{k}\right).$$ The divergence of the harmonic series makes it certain that this world record will go on reducing beyond any limit — although it will take an age to do it. To compute the number of years it takes to achieve a sub 9 second record we can use the approximation to the sum of a harmonic series, and solve the equation $$10-\frac{1}{10}\left(\ln{k} + \gamma\right)=9,$$ where $\gamma$ is the Euler-Mascheroni constant whose approximate value is 0.57721. As expected, we will have to wait a long time for a sub 9 second record: it will take 1,236 centuries. If you are interested in waiting for the time the record gets down to 0 seconds you will have to wait about $1.5 \times 10^{42}$ centuries.
This kind of calculation may seem unprofitable but it gives us a useful insight. If the reduction of the actual world record can match or better the minute reductions of the harmonic world record, there will be no limit to the actual record. This reduction will also take less time — though it will still be measured in millennia.

Olympic legend: At the 1936 Olympics Jesse Owens won gold in the 100m, the 200m, the long jump, and as part of the 4x100m relay team.
There is therefore the possibility that there is no limit to the world record and timings are inexorably on a downward path. Training methods continually improve, remarkable athletes appear on the scene. High altitude and a favourable (but legitimate) tail wind would also help. In the longer term there is the changing physiology of man along the lines of Darwin's theories. People who might one day run 5 second hundred metres will not be like people as we know them.
Another factor is involved. Since the passing of such historical legends as Jesse Owens, the recording of race times has become more accurate. With finer divisions and the introduction of hundredths of a second there is now an increased frequency of breaking records. The breakthrough in timing technology occurred in the 1960s when the American Jim Hines first broke the ten second barrier in the hundred metres with a time of 9.95 seconds at the Mexico City Olympics. While his record stood for 15 years, it has since been broken on twelve occasions.
What would prevent the record getting close to 0 would be if the reduction of the record year on year proved impossible, the determining factor being the physiology of human kind. If this is the case we may wonder where the limit will fall when athletes fail to improve the figure. This has intrigued sports scientists for generations as they watch athletic records go on tumbling year on year. From our experience it is unthinkable to imagine the record of 5 seconds which would mean a speeding ticket in a 40 mph zone. But logically we cannot rule this out: we just don't know.
A fruitful approach is given by a mathematical mode. Most models in this context attempt to fit data points to curves and from the asymptotic properties of the curve a deduction is made about a lower limit. One curve that has been used is the logistic curve, which is seen to fit the data accurately: the actual data either lies on this curve or is very near it. This curve also suggests a lower limit for the world record. The weakness of this data fitting is that there is often no appeal to sports science theory, and the approach leaves out physiology completely.
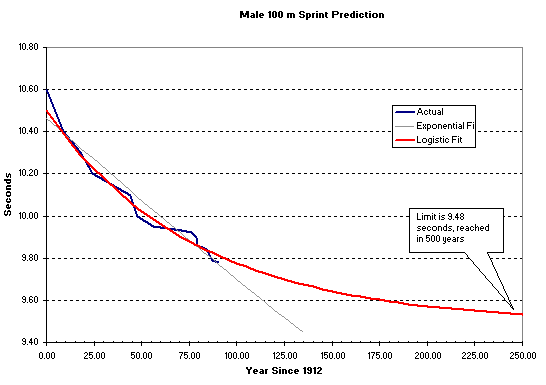
The blue line represents the actual world records for the men's 100m sprint between the years 1912 and 2002. The red curve is a logistic curve: it is the graph of a function of the form a/(1+be-cx) with the parameters a, b and c chosen so that the curve best fits the data. In this case the lower limit suggested by the logistic curve is 9.48s. Image: Kevin Duffy.
What is really needed is a scientific theory which links physiology to speeds. How do oxygen uptake, heart rate and the multifarious factors which contribute to running translate into a runner's speed? Not least to be taken into consideration is the additional motivation since the advent of monetary prizes. There is none for setting a record at the Olympics but Usain Bolt found himself $100,000 better off for posting 9.58 in the 100 metre event in Berlin. Does this have a bearing on the questions of when, where, and by how much world records are set?
Without such a theory all the predictions of a limit to the world record are pie in the sky. The model above predicts that 9.48 seconds is the limit beyond which humans cannot run. But then, we haven't yet seen what Usain Bolt can do.
About the author

Tony Crilly is Emeritus Reader in Mathematical Sciences at Middlesex University, having previously taught at the University of Michigan, the City University in Hong Kong and the Open University. His principal research interest is the history of mathematics, and he has written and edited many works on fractals, chaos and computing. He is the author of an acclaimed biography of the English mathematician Arthur Cayley and the internationally bestselling 50 Mathematical Ideas You Really Need to Know. His latest book, The big questions: Mathematics, is reviewed in Plus.
Comments
Anonymous
I remember reading something in Scientific American (in the 70's?) about the progression of records. I can't remember the details, unfortunately, but the conclusion was along the line that we aren't running quicker, as such (allowing for improvements in shoes, tracks, diet, etc) - but, rather, that we are able to run at the same speed for longer. For example, the average speed per mile for the world record marathon is roughly 4min 35sec per mile. This is the sort of time per mile that the top runners were doing for 10 miles only 40 years ago.
robert99
"What is really needed is a scientific theory which links physiology to speeds. How do oxygen uptake, heart rate and the multifarious factors which contribute to running translate into a runner's speed?"
These areas has been extensively studied for over 40 years.
Lloyd, Cavagna, Keller, di Prampero, Busso, Perronet-Thibeault, Duffield-Dawson, Pugh, Davies, Mureika, Press, McCardle etc.
Morton (2006) reviews over 120 papers in this field.
Anonymous
"extensively" is a relative term. Also, "extensively studied" does not guarantee that the problem is very well understood. There are other areas where there are hundreds of thousands of papers and they are still not well understood.
Anonymous
Thanks for the article, it's very interesting. One thing I noticed though is that the data points you have fitted your mathematical model to ignore Usain Bolt's achievements. According to your blue line, the world record is still 9.79 seconds. If you include Usain Bolt's marks of 9.69 followed by 9.58 (as well as some other intermediate marks by Asafa Powell I think), which have all been recorded still less than 100 years after 1912 along your x axis, then I think your model fit would be much less impressive, so if you added the latest data points and re-fitted a logistic curve the model would end up suggesting a maximum possible time of something lower (possibly around 9.40 seconds...)
Marianne
Yes it's true the model only uses data up to 2002. To include the latest world records one would have to fit a new model, that is, the parameters would change, resulting in a different curve.
Anonymous
An important factor in track and field records had been the competition between methods of doping and of doping detection. Endurance records dropped rapidly in the early 1990's with the availability of EPO, but then times increased when tests for first EPO and then CERA were added to antidoping protocols. This seriously confounds first order analysis. If Bolt's time trends are matched by competitors than I would suspect a new doing technique has been discovered which improves explosive power.
Anonymous
Presumably the 100m can't be done in less than about 33 microseconds, because that's how long it would take at the speed of light in a vacuum.