
Thinking outside the box
This article is the runner-up in the university category of the Plus new writers award 2009.
"Fine. The next person who comes in without having tried the exercise will lose not only the marks for this exercise, but for any previous exercises already completed in my class."
Hash words. I wasn't sure whether or not my maths professor had the power to do this, but he was definitely angry enough at his uncooperative class to try it. It wasn't our fault that the class was pass/fail.
Fast forward a week.

Where's your excuse?.
"So. Where's your exercise?" Obviously, I had been the one to forget. To make it worse, I was ten minutes late. The professor raised his voice, in order to better make a spectacle of me. "So what's your excuse?" I looked at the floor, about to mutter something about forgetting before taking my average-destroying punishment. He looked up over the top of his glasses, his anger at the whole class focused on me, and I decided that at least I would go out with a bang. "Go on, you can tell me," he urged, the calm before the storm. I took a deep breath and began to explain.
"It all began the weekend before last. Before that, I can assure you, I was a fairly normal person. But then, last weekend, I began to see things."
"Things? What kind of things?" the professor butted in, perhaps in surprise at my rather unusual response. I ad libbed.
It had been a rather ordinary Sunday afternoon, and I had been staring pleasantly into space lost in some kind of thought. Suddenly, and quite out of the blue, a sphere had appeared in the air in front of me. It had grown considerably larger, and then proceeded to shrink back down again until it disappeared.
I looked up to see the professor's response. He was busy drawing on the board. I turned to have a look at what he had sketched.
"Did you note precisely how the radius or volume of the sphere changed with time?" the professor enquired. Startled by the question, I looked up from his drawing and immediately replied that I had not. "That's a great pity," the professor replied. "You may have just had an encounter with a four-dimensional hypersphere." The rest of the class tittered, amused by my story and the professor's compliance with my game. He had drawn a three-dimensional sphere passing through a two-dimensional plane. To a two-dimensional person on his two-dimensional plane the sphere would have looked like a growing and shrinking circle. Just like my growing and shrinking sphere. So my growing and shrinking sphere was really just a three-dimensional cross section of a four-dimensional sphere moving through some forth dimension? I posed the question to the professor. "Of course there's no way of knowing for sure that it was a four-dimensional sphere, and not a four-dimensional ellipsoid with a spherical cross section, or some other four-dimensional solid with a spherical cross section, but had you timed how its radius changed with time, we could have assumed it was moving with a uniform velocity in the fourth dimension and at least had a better idea." He looked rather accusing, so I decided to continue with my story.
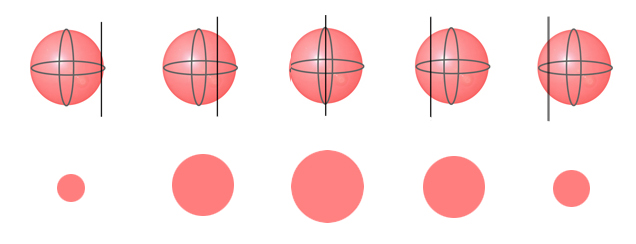
A sphere passing through a plane, represented here by a line. The intersection of the sphere and plane is a growing and then shrinking circle.
"I had just about convinced myself that I had imagined the whole sphere thing, when I tripped over a rather curious object on the floor. It looked like this," I quickly sketched a drawing on the board.

I explained that I had thought it was just a toy my little sister had left lying around, when it started to fold itself. I couldn't quite understand what I was watching, parts of it seemed to turn inside out and pass through each other, until it simply disappeared again.
"Ah, the tesseract!" The professor was truly pleased. The class looked truly confused. He explained.
"In one dimension the only geometric figure you can draw is two points joined by a straight line. In two dimensions a square arises from displacing a straight line segment along a direction perpendicular to the segment. Similarly you can form a cube in three dimensions by displacing a square. But why stop there? Why not have a fourth dimension? Now you can make a four-dimensional hypercube by displacing a cube perpendicularly in the forth dimension. It's called a tesseract!"
"We can't visualise the four-dimensional tesseract, but we can visualise its three-dimensional net. Just as a cube can be unfolded to give a two-dimensional shape that looks like a T, so the tesseract can be unfolded to give a three-dimensional object — that's the shape you mistook for your sister's toy."

A shadow of a tesseract rotating around a plane.
A student in the class piped up:"Physicists tell us that time is the fourth dimension, so is this the extra dimension you've just told us about the same as time?"
"No, but you can treat time mathematically like a fourth dimension. Time happens to have some very interesting physical properties that make it useful, in physics, to think about it like a fourth dimension: in this thinking the Universe can be described as Minowski space-time. It doesn't mean time is just like the other spatial dimensions". We all relented, and accepted what he said, even though we hadn't actually seen the equations.
"You haven't seen the equations yet! Why are you agreeing with me?!" He wrote on the board
"This quantity d describes the distance between two points in ordinary three-dimensional space: if you impose a coordinate system on the space so that one of your points corresponds to the coordinates (0,0,0) and the other to the coordinates (x,y,z), then Pythagoras' theorem tells you that d is exactly the distance between the two. There are three terms in this expression because there are three dimensions of space. According to general experience, and classical physics, this way of describing distance is the same whether you are on a moving train, boat or plane, or standing beside it watching someone on the moving object. In other words, it is conserved."
"This is no longer true in special relativity. Einstein showed theoretically that the distance d does depend on the velocity of your frame of reference, so d is no longer conserved! There is another quantity that is conserved though, and this is given by
where c is the speed of light and t is time. It makes time look a little similar to the physical dimensions x, y, and z, doesn't it? Of course, there's more to it than that," he continued, referencing a textbook.

A lightbulb is nearly spherical, so the inverse square law applies.
"Mathematically, there is no reason why you can't have extra spatial dimensions, it just so happens that physically we don't seem to have them. Take the inverse square law for electromagnetic radiation. If a point source, for example a light bulb, is emitting light, then there are P Watts of energy per second leaving the light bulb — P Watts must go through the spherical surface of the bulb per second. Since the surface of a sphere has area A=4πr2, where r is the radius of the sphere, the intensity is given by
Experiment shows that that this is indeed the case. If the world had four physical dimensions, then the inverse square law would be the inverse cube law, with the intensity falling off as 1/r3, since the light would emanate in four dimensions instead of three. Of course, light might not work in the fourth dimension (in fact, we've just shown that our kind of light doesn't), and there might be other reasons why we don't perceive a fourth dimension, but because none of our forces seem to work there, it seems likely that it would be very different from our three dimensions."
"So I'm crazy," I sighed sadly. The professor laughed. "Just a little. Anyway, let's give a big round of applause for our impromptu storyteller." As my face went from pink to crimson, I managed to breathe a sigh of relief, he didn't sound angry anymore, maybe I was off the hook. "We'll arrange your punishment after class." My heart sank, but at least I had gone out with the bang I had hoped for. After the lecture was over, the professor approached me. "That was the best lecture I have had so far with this class," he told me. "In exchange for losing no marks, I expect you to have another special topic prepared for us to talk about next week." Then he let me go. I left, amazed that I had managed to escape so lightly. I guess sometimes it doesn't hurt to think outside the box.
About the author

Sonia Buckley is a final year undergraduate at Trinity College Dublin, where she studies experimental physics (but don't worry, she loves maths too). She is about to begin a PhD in Applied Physics at Stanford University. When the physics gets too much for her, she likes to go hiking or rock climbing (or both).