The power of origami
Trisecting the angle using origami — proof
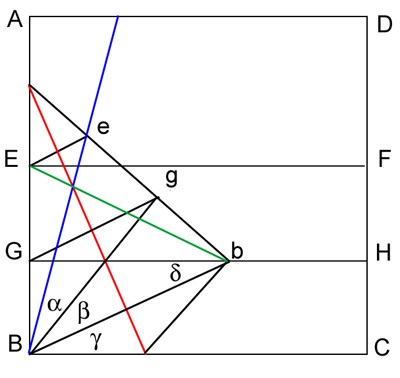
In the image on the right the angle between the blue line and the bottom edge is the angle to be trisected, and we must show that $\alpha = \beta = \gamma$. The red line is the crease resulting from the fold in step 4 of the folding sequence. Now look at the triangle $EBb$. We know that the length of the line segment $EG$ is equal to the length of the line segment $GB$, and we also know that the line segment $Gb$, which is the height of the triangle $EBb$, meets the line segment $EB$ at a right angle. In other words, the height $Gb$ of the triangle divides the opposite side into half. This means that the triangle $EBb$ is isosceles. The mirror image of the triangle $EBb$ when reflected in the red crease line is the triangle $ebB$, which is therefore also isosceles. The height of the triangle $ebB$ extending from the point $B$ therefore divides the angle at $B$ into half. This shows that $\alpha = \beta$. By mirror symmetry we have that $\beta$ is equal to the angle $\delta$ of the triangle $GbB$. And since the line $GH$ is parallel to the bottom edge $BC$, we have that $\gamma = \delta$. This proves that $\beta = \gamma$.