Next year will mark the tenth anniversary of the first draft of the human genome. It has provided tremendous insight into human genes, and formidable advances in biotechnology have accompanied this genomic breakthrough. However, the way these genes and their products interact with one another still has to be fully understood. Maths plays a central role in this understanding, partly because new biotechnologies produce vast amounts of data that have to be coped with somehow. But it's not just about quantity — mathematical models of genetic processes can provide qualitative insight into how things work. In our work at University College London a pretty straightforward model has helped to understand molecular processes that are relevant to cancer biology.

What does DNA do?

What causes a healthy cell to become cancerous?

DNA is important to the functioning of cells because it acts as a template for proteins, which are among the active molecular agents in cells. Turning the information coded in the DNA into proteins is not a straightforward process. There is an intermediary molecule, aptly named messenger RNA (mRNA), which is produced by a molecular apparatus called RNA polymerase. RNA polymerase reads the information on the DNA and produces mRNA molecules as it slides along the DNA. This first step is termed transcription and the mRNA molecule is called a transcript. A gene is a part of DNA that codes for a specific protein.

The second step is called translation. Here the mRNA molecule is treated by another molecular machine, the ribosome. It reads the mRNA to produce chains of amino acids, which when folded become active proteins. A single molecule of mRNA can be used several times to produce more than one protein.

Only a portion of the DNA codes for proteins and in certain organisms that portion is actually quite small. For example, in us humans, only 2% of the DNA codes for proteins. Another twist is that in an individual cell not all coding portions of the DNA are used. This is because individual cells in multicellular organisms typically perform specialised functions — a liver cell is different from a skin cell — so they don't need the entire coding repertoire contained in the DNA. In the same vein, not all proteins are being continuously produced, as some of them are needed on specific occasions only.

How is DNA switched on?

So, what causes a particular gene to be turned on — or expressed in biological jargon — in an individual cell? There are many factors that can influence gene expression, but a major role is played by special molecules called transcription factors. These attach to regulatory regions of the DNA and recruit the transcription machinery to express the adjacent gene. Transcription factors can also act as repressors, ie diminish the expression of certain genes. They can work in combination with other transcription factors, or bind to other non-coding sequences of the DNA.

If this wasn't complicated enough, transcription factors are proteins themselves, so they may arise from the work of other transcription factors or cause their appearance. These chains of transcription factors can branch back onto themselves, creating feedback loops.

In summary, life at the molecular level is rather baroque and understanding how complex networks of genes and proteins are connected and function is one of the major challenges of contemporary biology.

DNA repair

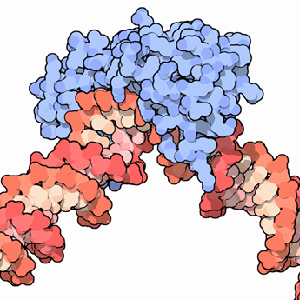
A transcription factor (blue) binding to DNA (red).

One system that's particularly interesting, and linked to the formation of cancer, is the DNA damage response network. When a cell's DNA has been damaged repair mechanisms systematically spring into action. But these mechanisms don't always get things right. They can commit errors, which can lead to cancerous mutations threatening the whole organism. To try and avoid such danger, a cell affected by a potentially dangerous mutation has the option to commit suicide — called apoptosis — for the greater good.

One transcription factor that's heavily involved in directing these voluntary cell deaths is called p53. It has been found to be mutated in about half of human cancers. So if we can understand exactly which genes p53 helps to express, then this could help to find ways to fight the disease.

Finding target genes

Identifying the target genes of p53 involved some mathematical detective work. The extent to which a given gene is being expressed in a particular cell can be measured by looking at the concentration of mRNA in the cell — the more mRNA there is, the more the gene is being expressed. If p53 is implicated in the expression of the gene, then a high concentration of mRNA should coincide with high activity of p53, and a low concentration with low activity.

We can make this intuition precise using a differential equation (if you haven't come across a differential equation before, look at the box on the right):

$dx/dt = B+Sf(t)-Dx(t).$ Here the function $x(t)$ describes how much of mRNA there is at time $t.$ The left hand side of the equation is the derivative of $x(t)$ with respect to time: it describes the rate at which the quantity changes over time. According to this equation, the rate of change of the mRNA quantity is the sum of three terms. The first ($B$) corresponds to a constant - or basal - rate of mRNA production (the bathtub equivalent is an open tap no one fiddles with). Each gene comes with its own constant $B$. The second term is more interesting, as it can vary over time. It's a product of two things. The first is the component $f(t),$ which describes the transcription factor activity. It's a sort of profile of how p53 behaves, which is independent of the particular gene we're looking at. The second factor is a constant $S$. This constant is specific to the gene, and describes to what extent p53 is involved in mRNA production. For some genes, this constant will be close to zero, indicating that the transcription factor has little or no influence whatsoever on that particular transcript's production. We are of course interested in those genes that are sensitive to the transcription factor activity, namely those that have a sensitivity constant $S$ that is significantly greater than zero. The third and last term ($Dx(t)$) describes the loss (or degradation) of mRNA, hence the negative sign attached to it. This corresponds to "leaking" mRNA molecules. (Actually, leaking is not quite the right word: the mRNA molecules may be chopped up before having a chance of being translated into proteins, rather than literally leaking out of the cells. But in any case, they disappear.) The rate of loss of mRNA is not constant, but proportional to the quantity $x(t)$ of molecules that are present there and then (in contrast to the bath tub analogy). This is because more molecules are likely to be degraded if more are present in the cells. That's why the constant $D$ is multiplied by $x(t).$

Finding target genes of p53 is a reverse bathtub problem.

This model now gives us a strategy for finding out whether p53 is involved in the expression of a given gene. Using microarrays we can measure the quantity $x(t)$ of mRNA over time, and the rate $dx/dt$ at which this is changing. We can then try and find constants $S,B,$ and $D$ which make the equation work. The dependency status of individual genes to p53 is captured by the sensitivity to the transcription factor activity, which is described by the parameter $S$ in the model. To be a potential target, the sensitivity has to be quite large, and the model has to fit the data well enough.

(Note that this situation is different from our bathtub example. With the bathtub, we knew all the constants that made up the equation, and were after the function $b(t),$ which described the state of the system at time $t.$ In this case we know the state of the system, given by $x(t),$ and are after the constants that make up the equation. In some sense, this is an inverse problem, and this kind of endeavour is indeed often called reverse engineering.)

The missing link

So far, so good, but it turns out that we're actually missing a crucial bit of information – the transcription factor profile described by the function $f(t).$ Trying to deduce $f(t),$ as well as $B, S,$ and $D$ from the data at hand would involve creating more information than there was to start with, the mathematical equivalent of creating perpetual motion. But thankfully, p53 is an important transcription factor and fairly well-documented. Some of its target genes are already known. Using this information and fitting a handful of the known target genes to our model, we were able to deduce the activity profile $f(t)$ of p53. That activity profile was then used to fish out potential targets of p53: these were genes whose expression profiles fitted the model well, and had a high sensitivity constant $S.$ Our predictions were later confirmed by an independent experiment – the genes we identified really were targets of p53. The icing on the cake was that a significant proportion of those confirmed predictions were of genes that weren't previously known to be p53 targets. Knowing targets of a single transcription factor is admittedly only a portion of the bigger picture sketched above. For example, p53 is only one among several transcription factors that is being activated upon DNA damage. By rearranging our model for gene expression and combining it with transcript turnover rates, we have been able to extract the main transcriptional activities governing the cellular response to stress. We are now working on trying to understand how these activities combine in stressed cells. In summary, a lot remains to be done to fully understand this system (and others) but there is little doubt mathematics will play a central role in this process.

About the authors

Martino Barenco

Martino Barenco is a mathematician at the Institute of Child Health. After working for seven years as an economist in Switzerland, he came to London to study chaos theory. He is still in Britain because he likes the local sense of humour and the weather.

Mike Hubank

Mike Hubank is a Senior Lecturer at The Institute of Child Health, University College London.