What is DNA?

The double helix of the DNA molecule has two strands, each of which is made up of four basic building blocks, called nucleotides, denoted by the letters A, G, T and C. The order of these bases contains the instructions for an organism's development and functioning. The order of bases on one strand defines the order of bases on the other: a A or G on one strand corresponds to a T or C (respectively) on the other. Thus, it's sufficient to know the sequence of one strand, so we will ignore the double stranded nature of DNA in this article.

Image: US National Library of Medicine.

The genomes of two humans are 99.9% identical, which is why we can talk about sequencing "the" human genome.

Genomics is an area where size really does matter. The first draft of the human genome was completed by the International Human Genome Consortium ten years ago. It is represented by around 3 × 10⁹ bases — that's a sequence of A, C, G, and Ts around 3,000,000,000 digits long. With such large numbers, sequencing the entire genome of a complex organism isn't just a challenge in biochemistry. It's a logistical nightmare.

Sequencing techniques can only sequence DNA strands up to 1,000 bases long. To deal with longer strands, all you can do is break them up into shorter pieces, sequence these separately, and then try and re-assemble the lot. It's like a massive jigsaw puzzle with hundreds of thousands of pieces. Some of the largest non-military supercomputers have been built just for the purpose of solving it.

The shotgun approach

One technique that's been at the heart of efforts to sequence whole genomes is called shotgun sequencing. It involves randomly breaking a strand of DNA (whether it's the whole genome or a shorter strand) up into smaller fragments, around 2,000 bases long. Usually both ends (though sometimes just one end) of each fragment are then sequenced, giving a pair of reads for each fragment, with each read being around 500 bases long. In practice you don't start with a single strand, but with many identical copies of it, each of which is randomly fragmented. The fragments coming from different copies overlap each other (bits of two fragments can correspond to the same part of the original strand), so you end up with layers of overlapping reads (see the figure below). These should hopefully cover most of the original DNA strand. The overlaps between reads should then give you enough information to re-assemble it.

The DNA strand (grey bar) is broken up into fragments (blue bars including red ends), which are sequenced at one or both ends (red ends). This is done to several copies of the original strand, creating layers of overlapping reads.

This sounds good in theory, but in practice you immediately encounter a mathematical problem. If your initial DNA strand is long, you're looking at a large number of reads that need to be compared to see if they overlap. For the whole human genome, you're looking at up to 50 million reads — comparing every read to every other read gives you around 50,000,000² sequence comparisons.

That's a very large number, but it gets worse because any sequencing technology is prone to making errors. When sequencing a read, your process may well miss out a character, or get one wrong, or insert one that shouldn't be there. So rather than looking for parts of the two sequences that match exactly, you're looking for parts that match reasonably well.

For example, the two reads GATCCA and GTGCCT look very different, but if you allow for gaps and the occasional mismatch, you see that they might well represent the same stretch of DNA:

Aligning two sequences — finding the best way of matching a character in one sequence with a character, or a gap, in the other — is a major computational challenge. A brute force approach might involve looking at every possible alignment and checking how good it is. In our example, where each read contains six characters, this would mean checking 8,989 possible alignments. If your reads contains 107 characters or more, which is realistically the case, the number of possible alignments is larger than 10⁸⁰ — that's more alignments than there are atoms in the observable Universe!

Dynamic programming

But luckily, you can do better than brute force. At the heart of many genome assemblers lies an ingenious little algorithm, known as dynamic programming. It's been around since the 1950s and it's extremely versatile: it's used to enable companies to make optimal decisions, and computers to understand music and recognise the human voice.

To use dynamic programming to align two sequences, write one of them horizontally and the other vertically, to form a grid of cells. Each cell corresponds to a pair of characters, one from each sequence. Put a cross in each cell which corresponds to a matching pair. Overlapping parts of the sequences give rise to a line of crosses sloping downward from left to right. If the sequences match exactly, this line goes straight down the diagonal, if they are offset against each other, the line lies off the diagonal.

A line of crosses which jumps one cell to the right or down in places indicates that the sequences could be aligned by inserting a gap:

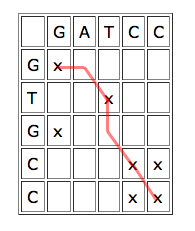The red line corresponds to the alignment G A T - C C G - T G C C

Finding optimal alignments translates to finding the "best" runs of matches. "Best" doesn't necessarily mean straight: if you're tolerant of the occasional mismatch or gap, then a long run with some holes or jumps may lead to a better alignment than a shorter line of exact matches. Just how tolerant you are of gaps and mismatches depends on how likely your technology is to make these errors.

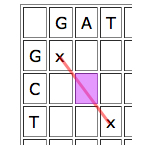
Dynamic programming works by looking at the cells one by one and giving each cell a score depending on how well it contributes to any runs of matches that indicate good alignments. The idea is quite simple. Given a particular cell, first look at the cell that meets it at its top left corner. If that "parent cell" is part of a good run of matches (that is, if it has a high score), it's worth considering if you can continue it, even if your particular cell represents a mismatch, and definitely if it represents a match.

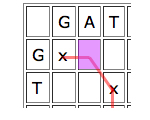
Then look at the parent cell directly to the left. If this is part of a good run of matches, then it might be worth aligning the entry of the horizontal sequence corresponding to your cell to a gap, and see how you go from there.

Similarly for the cell just on top, only in this case you would align the vertical entry corresponding to your cell to a gap.

If you're scoring cells left to right and row by row, then each of these three parent cells will already have been given a score by the time you reach the cell you're looking at. You compare the scores of the three parent cells and deduct penalty points for a mismatch or gap and add bonus points for an exact match. You then choose the biggest of the three numbers coming from the parent cells after adding or deducting points, and that's the score of your cell. The box below contains the exact rules.

Dynamic programming rules

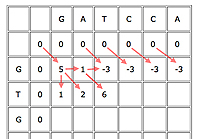
An example with the first few cells filled in.

First, insert a row of 0s at the top and a column of 0s on the left. This is just to initialise the algorithm, as cells in the first row and column don't have all of their parents.

Now suppose your current cell is C. Let b(C)=5 if the cell corresponds to a matching pair of entries, otherwise b(C)=-3. In other words, we award 5 bonus points for a match and deduct 3 for a mismatch. Let's say that the penalty for a gap is -4.

Write D(C) for the parent cell that's diagonally on top and to the left, T(C) for the cell directly on top, and L(C) for the cell directly to the left. The score of C is

Score of C = max{score of D(C)+b(C), score of T(D)-4, score of L(C)-4}.

When you've finished working out the score for each cell, keeping track of where each cell got its score from, you get a table looking like this:

The blue path gives the alignment
GAT-CCA
 G-TGCCT.

You can now easily find the best alignment (best according to your scoring rules). Simply find the cell in the last row or column that got the biggest score, see from which of its three parents it got the score, and continue working backwards to obtain the alignment. Every time you move directly up or to the left, you know that the alignment contains a gap.

Dynamic programming drastically reduces the number of steps needed to compute the best alignment of two sequences. If the sequences are each n characters long (though they don't in general need to have the same length), you only need to do some simple arithmetic for each of the n² cells, and then work backwards to construct the alignment. In other words, the number of steps is proportional to n², which is a lot less than the vast number of possible alignments that need to be checked in the brute force approach. For n=6 as in our example, it's 36 compared to 8,989. If you know that your sequencing technology is unlikely to make many errors, you can reduce the number of steps of the algorithm even further. What's more, dynamic programming allows you to stipulate how errors and gaps should be penalised, so you can decide exactly what you mean by a "best" alignment, depending on the error rates of your technology.

Sequence assembly

The next task is to assemble the whole sequence. Essentially, this involves merging reads with strong overlaps, to build up longer and longer sequences, until you've covered the entire DNA strand, or at least enough of it so that gaps can be filled in individually. The biggest problem in this context are repeated sequences, because they give rise to ambiguities. And unfortunately the human DNA sequence is full of repeated sequences of different types.

The initial approach to sequencing large genomes, used by the International Consortium, involved applying a shotgun method not to the whole genome, but to smaller pieces, known as BACs. These are 100,000 to 150,000 base pairs long. With that length, a BAC holds enough biological clues to tell you where on the genome it belongs, and it's short enough for each individual BAC to contain relatively few internal repeats.

At first people thought that the shotgun process was unsuitable for whole genomes, as repeats would hopelessly confuse any assembly algorithm. However, with increased computing power, researchers decided to have a go, making clever use of all the information that comes with the shotgun process. This includes, for example, the fact that reads come in pairs (if every fragment of the shattered DNA is sequenced at both ends) and statistical information on error rates and how many reads are likely to correspond to a given piece of DNA.

The new algorithms made shotgun sequencing for whole genomes feasible and it was used by the International Consortium, as well as commercial companies, as part of their efforts.

Next generation sequencing

When the International Consortium started on its draft of the human genome the very act of producing a read from a sample of DNA was extremely expensive and time-consuming. The 35 million reads needed for the Human Genome Project took years to generate. In the last few years, however, there has been a revolution in sequencing technology. Methods now exist that can produce more than 100 million reads a day and are relatively cheap, too. However, the reads they produce are very short, for some technologies less than 50 base pairs long. Originally, short reads were of little use for sequencing whole genomes. You need more of them, which means more computing time, and with lots of very small bits it's harder to disambiguate repeats.

However, the new technology prompted people to look at short reads again, even for sequencing whole genomes. Several algorithms that have been developed in the last five years make clever use of an ingenious approach going back to the 1990s. Rather than looking at whole reads, this approach concentrates on short strings of some length k. First, you find all k-strings that occur in one or more of your reads. You then lay them out as a graph: each k-string is a node of the graph, and there's an arrow from one k-string to another if the last k-1 characters in the first are the same as the first k-1 characters of the second and if the merged version of the two strings appears in one of the reads.

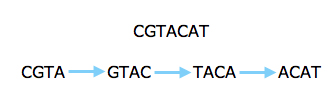
The read above can be split into strings of length four and represented by a graph.

Assembling the original sequence corresponds to finding a path through your graph which traverses every arrow once. If you are lucky, there is only one such path, which then gives you the whole sequence.

For large genomes, though, errors and repeats mean that you'll never be that lucky. One algorithm, which forms the basis of an assembler called Velvet published in 2008, makes clever use of the structure of the graph to weed out errors and identify repeats.

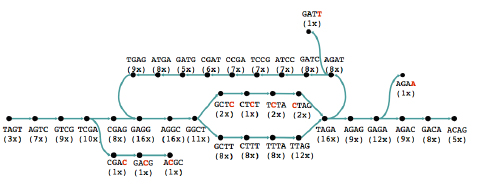
A graph representing reads of a sequence. The number underneath each string indicates in how many reads it occurs. Image: Daniel Zerbino.

The basic idea is that a sequencing error at the end of a read gives rise to a "tip" in the graph: that's a short dead end where the graph doesn't continue. This is because the exact same error will only occur in very few reads, so you'll run out of k-strings to continue the tip. Errors that occur within reads will give rise to "bubbles", alternative routes between two nodes.

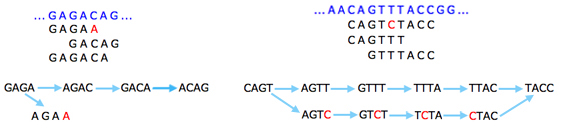
Sequencing errors (shown in red) give rise to tips (left) and bubbles (right).

When you look at your graph you can spot which tips and bubbles are likely to come from errors by keeping track of coverage: since the same error is only going to appear in very few reads, the nodes containing the error will also correspond to very few reads. So you go through your graph, pruning off tips with low coverage and flattening bubbles by removing whichever route has lowest coverage.

After this you can merge nodes where there's no ambiguity. Any loops in the graph now indicate repeated sequences. If it's not clear from the graph how to resolve these repeats, you can make use of extra information, for example on paired reads from opposite ends of a fragment, to deal with them.

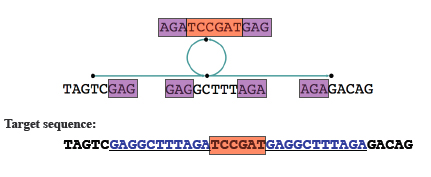
The loop in this case indicates repeats, shown in blue in the target sequence. Image: Daniel Zerbino, modified by Gos Micklem.

Algorithms like this one are now being used for large genomes and they speed things up considerably: sequencing work that previously took days and thousands of computers working simultaneously can now be done in a day on just one computer with a large memory.

How do you know it's correct?

Sequencing whole genomes is an inexact science. No sequencing technology is 100% accurate and highly repetitive strings in the genome can be very difficult to resolve. No genome assembler can produce one sequence that's definitely the correct one. Biological information, for example comparing sequences for various individuals, obviously helps, but statistics also plays an important role because it can quantify levels of uncertainty. Using experiments, you can estimate how many errors sequencing technologies and algorithms are likely to make. In fact, statistical information on the likelihood and distribution of errors is used by many algorithms to try and weed them out. By keeping careful track of these error rates, you can measure just how confident you are of your results.

The final version of human genome published by the International Consortium in 2003 covers around 95% of the the genome (the remaining regions are highly repetitive). These 95% have been sequenced with more than 99.99% accuracy: only one in 10,000 bases is likely to be wrong.

What's next?

So what's next for genome sequencing? Some people have pointed out that recently sequencing technology has developed in the wrong way. It's become faster, but the short reads produced make the assembly problem much harder. Maybe future technologies will be able to sequence longer and longer strands of DNA. But until they can sequence a whole genome in one go, lots of computing power and clever algorithms will be needed to piece the pieces together, and mathematics will remain at the heart of genomics.

About the author

Marianne Freiberger is co-editor of Plus. She thanks Gos Micklem, Director of the Computational Biology Institute at the University of Cambridge, for his time and patience in explaining DNA sequencing to her.