
The origins of proof II : Kepler's proofs
As we explained in The Origins of Proof, Part I in Issue 7 of PASS Maths, the concept of a "proof" was developed in the field of geometry by the Greeks. The Pythagoreans and Euclid were among the mathematicians who developed the idea of abstract deduction. But during the Renaissance the philosophy of nature increasingly came to rely upon mathematics to help to explain the Universe and its workings.
Astronomy had previously been a branch of mathematics, that is, the business of astronomers was only to provide the means of calculating the positions of planets (as seen against the background of the fixed stars). Kepler brought astronomy into natural philosophy by proposing to find the actual paths of the planets in relation to the Sun which, following the theory put forward by Nicolaus Copernicus (1473 - 1543) in 1543, Kepler believed to be in the centre of the Universe and the body around which the planets (including the Earth) revolved. Thus, mathematician though he was, Kepler was doing what we should now call Physics. To find the paths of the planets he would need to use innovative forms of mathematics; and he tried to make his proofs as obviously sound as possible by spelling the steps out in detail and emphasising the physical basis for his mathematical procedures. Of course, his proofs are not what we would now call "proofs" in Mathematics, as they were based on data collected from observations - but they are mathematically rigorous and they introduce the crucially important notion of observational error. From then on astronomers learned to ask not whether a theory was right or wrong but whether it fitted the observations to within the known margin of error. Kepler's methods influenced the thinkers of the time, and are an important step in the development of proof as we know it in Science today.

Figure 1: Portrait of Kepler, engraving by Jakob van Heyden.
Johannes Kepler (1571 - 1630) is now chiefly remembered as a mathematical astronomer, in particular for discovering three laws that describe the motion of the planets. In their modern forms, these are
- The path of each planet is an ellipse with the Sun at one of its foci.
- As the planet moves along its path, a line joining the planet to the Sun sweeps out equal areas in equal times.
- For any two planets, the ratio of the squares of their periods of revolution about the Sun is the same as the ratio of the cubes of their mean distances from the Sun.
These are usually known as "Kepler's three laws of planetary motion". It was from the third law that Isaac Newton (1642 - 1727) was to deduce the existence of an inverse square law of gravitation (in Mathematical Principles of Natural Philosophy or, to give it its Latin title, Philosophiae Naturalis Principia Mathematica, London, 1687).
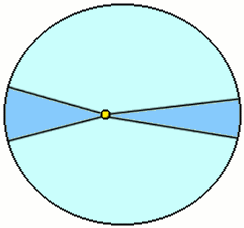
Figure 2: Diagram to show what is now known as Kepler's second law (the area law). The darkly shaded areas are equal, and are swept out in equal times. The planet moves faster when nearer the Sun.
Kepler published the first two laws in 1609 in a work aptly titled New Astronomy. The third appeared ten years later in a book about cosmology, called The Harmony of the World. Both of these works are now available in English translation (see the bibliography) but neither is exactly an easy read. Indeed Kepler himself admits as much in the New Astronomy, saying in the second paragraph of his Introduction:
I myself, a professional mathematician, on re-reading my own work find it strains my mental powers to recall to mind from the figures the meanings of the demonstrations, meanings which I myself originally put into the figures and the text from my mind. But when I attempt to remedy the obscurity of the material by putting in extra words, I see myself falling into the opposite fault of becoming chatty in something mathematical.
[trans. JVF]
It is good to know one has the author's permission to find the mathematical reasoning difficult to follow.
The New Astronomy was printed as a large folio. In an effort to make it look attractive, the publisher added some decorations to the diagrams. Modern readers may not find the effect totally reassuring. Indeed, it seems that on the whole Kepler's contemporaries also found the work difficult. The reason for this was to do with how Kepler set about proving that planetary motion could be described by the two laws. This method was new. It was, in fact, new to Kepler as well as to his readers. So we shall start by having a look at what he was taught about mathematics.
Kepler's early years and his education
Kepler was the eldest child of an innkeeper's daughter and a mercenary soldier. His father never returned from a military campaign he joined when his son was about six. So Kepler's childhood was spent in his grandfather's inn. He tells us he used to help serve customers there - which no doubt provided practice in arithmetic.
However, Kepler also got a conventional education, first at schools and then at the University of Tübingen. In consequence, his ideas about what made for a good proof were very solidly based on Euclid. That is, we may expect to find series of definitions, followed by what Kepler calls axioms (but Euclid called Common Notions and Postulates - see The Origins of Proof, Part I in Issue 7), followed in turn by deductive proofs. In most of his works, Kepler does his best to set all arguments out in this way. No doubt he thought it was clear, as well as visibly rigorous. All the same, he follows the habits of his time in not always filling in all the details.
The mathematical methods that Kepler employed in his proofs were generally also closely based on Euclid. And that includes the proofs in the New Astronomy.
The orbit of Mars and the first two laws
Kepler was not studying planetary motion in general; he was engaged on the specific task of finding an orbit of Mars - that is, a mathematical model for its motion. This process took about five years, and there are 987 surviving folio pages of arithmetic. So it is hardly surprising that, while Kepler's full title for what we are calling the New Astronomy mentions "commentaries on the motion of the planet Mars", in his more personal reflections Kepler - obviously mindful of Mars being the Ancient Roman god of war - refers to his construction of the orbit as "my war with Mars".
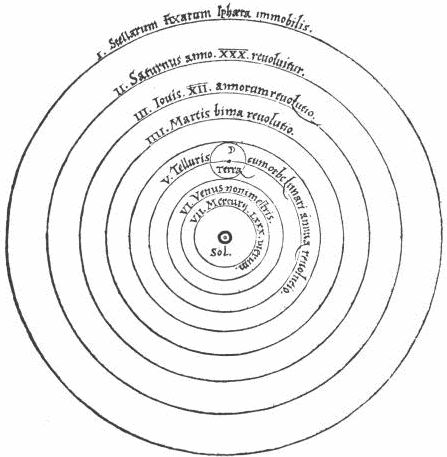
Figure 3: Nicolaus Copernicus, De revolutionibus orbium coelestium (On the revolutions of the celestial spheres). The Copernican system of the world, in which the Sun is at rest in the centre of the Universe. Copernicus shows only the order of the spheres. There is no attempt to show their relative sizes.
As we know, it ended Kepler 1: Mars 0. And that turned out to be the final in regard to the motion of the planets. In 1687, Isaac Newton used Kepler's three laws to help him give a mathematical explanation of the Solar system. That is the happy ending. Kepler had done his bit towards proving that Copernicus was right to say the Earth went round the Sun (see figure 3). Kepler had been a Copernican ever since his student days at Tübingen.
Constructing an orbit from circles
However, on the practical level, in considering the orbit of Mars, there was a serious problem of proof. And it was a new problem, too.
Until then, scholars who attempted to explain the workings of nature ("natural philosophers") had taken it for granted that for a motion to be eternal, as the motions of the planets obviously were, they must be uniform. Their being uniform meant that no point in time and no position in the path was special, so there was no need to look for a beginning or an end. Here we have a relic of the Ancient, pagan, idea that the Universe had neither beginning nor end in time (though it was considered finite in spatial extent). In fact, since the orbits showed a strict periodicity, the idea was that the motion of each body should be uniform and circular.
However, this satisfying idea - which we know about from the fourth century BC onwards - was rapidly overtaken by astronomical observation, and by the time of Claudius Ptolemy (who lived in Alexandria and is known to have made astronomical observations in the period 129 - 141 AD) astronomers constructed the orbits of planets by combining circles, the centre of one riding on another, and there were various compromises made about what counted as uniform motion. All the same, natural philosophers continued to believe they had got the basic principles right.
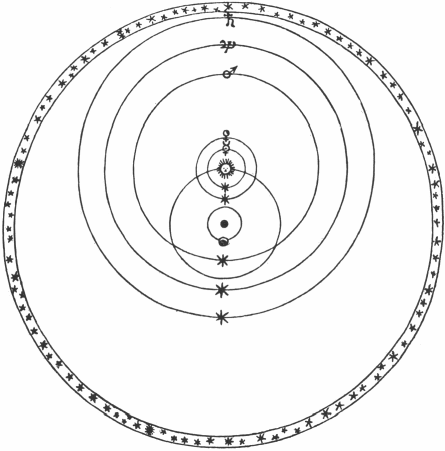
Figure 4: Tycho Brahe, De mundi aetherei recentioribus phaenomenis (Recent phenomena in the aetherial world), Uraniborg, 1599. The system of the world which Tycho believed was correct, in which the Earth is at rest in the centre of the Universe.
Tycho Brahe's observations
Kepler had a huge number of observations to work with. These had been accumulated by Tycho Brahe (1546 - 1601). Tycho wanted to reform astronomy, but seems to have been unclear how this was to be done - except that it would involve a lot of observations and proving the truth of his own description of the planetary system, in which planets circle the Sun, which in turn moves round the stationary Earth (see figure 4). One is (I think) entitled to wonder whether one reason why Tycho went on making more and more observations was because that put off the day when he had to think about how to use them. As it happened, he simply decided to hand that part of the work over to assistants. And in the event he left it too late: he did not live to see Kepler's success. In fact, he might not have been entirely pleased about it, because Tycho did not believe Copernicus was right, whereas Kepler's laws shout at us that Kepler did.

Figure 5: Tycho Brahe, Astronomiae instauratae mechanica (Apparatus for the foundation of astronomy), 1598, mural quadrant (constructed in 1582). As the name implies, the instrument is part of the wall. The scale, radius 1.94 metres, is made of brass, and inside it there is an elaborate painting showing Tycho at work in his observatory (which has an alchemical laboratory in the basement). Two assistants are shown beside the quadrant helping to record the time of the observations. One reads the clock and the other writes down the reading.
Click here for a higher resolution image of the mural quadrant.
Kepler first encountered this mass of planetary observations when he came to Prague as Tycho's assistant, in 1600. As we shall see, he must have discussed with Tycho how accurate the observations were. Tycho seems to have told him that they could be relied upon to five minutes of arc. (One degree of arc is divided into sixty minutes, each of which is divided into sixty seconds.) In fact, Tycho's observing instruments (see figure 5) were exceedingly well-designed, and neither expense nor trouble was spared in their construction and in improving their performance. Modern checks - comparing Tycho's observed positions with positions of planets found by modern calculations (computer-assisted of course) - show that Tycho was right about how good they were. The limit is about that imposed by the resolving power of the human eye. (The telescope came into use for astronomy only after Tycho's death.)
Kepler's calculations
Kepler's account of his calculations in the New Astronomy is certainly not a full diary of what he actually did, but there is good reason to suppose that it does, in outline, follow the actual progress of his reasoning. We know, therefore, that the law we call the second (sometimes also called the "area law") was in fact arrived at first.
The area law
As his calculations progressed, Kepler was able to use exact geometrical methods to find areas. But at first finding the areas was a difficult task, and Kepler's method was approximate, effectively adding up areas of triangles with their vertex at the Sun and very small vertical angles, as shown in figure 6. Kepler used triangles whose vertical angle was one minute of arc. His method is best near the apsides, that is the positions at which the planet is nearest to or furthest from the Sun, which (once he knows the shape of the path) will turn out to be the ends of the major axis of the ellipse. The calculations are made more difficult by having to allow for the motion of the Earth, which is, of course, not in the same plane as the motion of Mars. (The planes of the two orbits are inclined to one another at about 1 degree 50 minutes.)
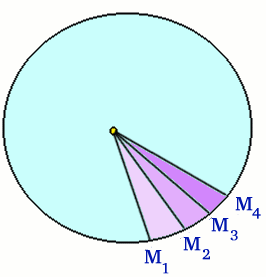
Figure 6: Finding the area swept out by a line joining a planet to the Sun. The points M1, M2 etc. represent positions of Mars. S is the Sun.
Kepler's method of finding areas is, as he says, similar to that used by Archimedes (c.287 - 212 BC) to find the area of a circle. But it is not exactly the same, and unlike Archimedes' procedure, Kepler's is not completely rigorous. However, Kepler's method does, also, look a little like integration, and it did in fact mark the beginning of a technique called "the calculus of indivisibles" which is now seen as an ancestor of modern calculus.
Anyway, by Chapter 40 of his book, Kepler had decided the area law was good enough to go on with. He used it as a way of measuring time.
The ellipse
The shape of the curve also gave trouble. Essentially, Kepler had to try different shapes, using a certain number of observations to find the curve, then use the curve to find some more positions, for times when he had observations available, and then check whether these calculated positions agreed with the observed ones. He arrived at the ellipse at the end of Chapter 58:
My argument was as in Chapters 49, 50 and 56: The Circle of Chapter 43 is wrong because it is too large, and the ellipse of Chapter 45 is too small. And the amounts by which they respectively exceed and fall short are the same. Now between the circle and the ellipse there is no other intermediary except a different ellipse. Therefore the path of the planet is an Ellipse; ...
[New Astronomy, Chapter 58]
This passage marks sudden death for about two thousand years of using circles in astronomy. However, Kepler simply carries on with his work. He is, moreover, aware that the ellipse is an idealisation. In a letter to a friend he had said
the most true path of the planet [Mars] is an ellipse, ... or certainly so close to an ellipse that the difference is insensible.
[Kepler to David Fabricius, 11 October 1605]
That is, he recognised that he was always working with approximate values - even if he was looking for an exact geometrical figure to describe the path.
Error and approximation
On the other hand, he knew the size of the errors in Tycho's observations, and used this to establish how closely theory must agree with observation. This raises another problem, one which Kepler himself had not noticed. He assumed that the error in values calculated from an orbit based on observations would be the same as the errors in the original observations. This agreement is in fact crucial to his whole proceeding.
We now know it is not true that the calculated orbit will necessarily have the same accuracy as the observations used to construct it. So-called "chaotic" behaviour of quite simple functions shows that small errors in input can become huge variations in output. However, Kepler was lucky. Well, perhaps not merely lucky: he was, after all, carrying out all these calculations by hand, so he could see that they were, as we would now put it, "well behaved".
The New Astronomy has seventy chapters (337 pages in the original edition). By the end, Kepler has - in the opinion of competent historians - established the elements of an orbit of Mars that agrees with the modern one so closely that in making the comparison allowance has to be made for the small changes that have occurred in the orbit since Kepler's time. (These changes, called "secular changes", are mainly due to the gravitational pull of Jupiter.)
Assumptions and arithmetic
Kepler's first two laws were discovered in the course of his finding the orbit of a planet - a standard task for an astronomer, though, as we have seen, in this case there was the complicating factor that Kepler had a huge number of observations at his disposal. He naturally wanted to make the best possible use of them. In order to do so, he made as few assumptions as possible about the shape of the path. The repetitious mass of Kepler's constructions and computations is daunting, indeed so daunting that it is hard for anyone to understand how he could have kept his head as he worked his way along the line of reasoning. But he did. And the method of repetitious trial and error, converging toward an acceptably accurate answer, has the advantage that errors of calculation will show up at the next stage. A computer would have helped, though.
In fact, the analogy with the iterative procedures of programs written for electronic computers did tempt a twentieth-century astronomer to try a machine simulation of Kepler's procedure. He incautiously entitled the resulting paper "The computer versus Kepler" and concluded that Kepler had been clumsy, needing more iterations than the machine had. However, a few years later the same astronomer published another paper, called "The computer versus Kepler revisited", in which it was confessed that there had been a mistake, and Kepler had in fact done at least as well as the computer.
In Kepler's day, astronomers took it for granted that they would need to do a lot of arithmetic, and assistants were sometimes employed to help with the routine work. However, it was exactly at this time that people were making the first attempts to build machines to carry out arithmetical operations automatically. An abacus does not qualify because you have to push the beads (or move the counters).
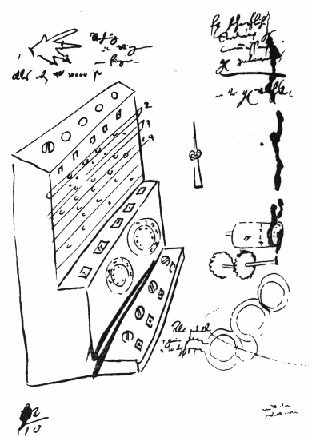
Figure 7: Wilhelm Schickard's calculating machine, a sketch by Schickard enclosed with his letter to Kepler dated 7 March 1624.
Among the first of these machines for carrying out arithmetic was one designed by Kepler's friend Wilhelm Schickard (1582 - 1635), who was a professor of mathematics at Tübingen (see figure 7). Some letters survive in which Kepler and Schickard discuss this project, and it seems rather likely that Kepler contributed some ideas to the design. The machine, like most others of the time, never got much beyond a working prototype. However, it is interesting, and novel, in being designed to lose numbers from the right when answers came out with too many figures to be accommodated in the machine. Perhaps that idea was more likely to occur to an astronomer? Astronomical calculations very often involve working with long numbers.
The third law
Kepler's third law, which relates the periods of planets to the sizes of their orbits, is really a law describing the structure of the Solar system. It was in his first book on cosmology (1596) that Kepler had first mentioned the desirability of finding such a relationship. So it is appropriate that the law did indeed first appear in his next work on cosmology. But that was many years later, in 1619, and the law only just made it: Kepler discovered it only after the book was almost finished. As he explains
...if you want the exact moment in time, it [the correct form of the law] was conceived mentally on 8th March in this year one thousand six hundred and eighteen, but submitted to calculation in an unlucky way, and therefore rejected as false, and finally returning on the 15th of May and adopting a new line of attack, stormed the darkness of my mind. So strong was the support from the combination of my labour of seventeen years on the observations of Brahe and the present study, which conspired together, that at first I believed I was dreaming, and assuming my conclusion among my basic premises. But it is absolutely certain and exact that the proportion between the periodic times of any two planets is precisely the sesquialterate proportion of their mean distances..."
[Harmony of the World, Linz, 1619]
At the end of the final (fifth) book of the Harmony of the World Kepler notes that the work was finished on 27 May 1618, and the fifth book was revised "while it was being printed", the revisions being completed on 19 February 1619. The revisions were of course occasioned by the discovery of the Third Law, which plays a significant part in the final version.
As the quotation above makes clear, checking that the squares of the periods were proportional to the cubes of the mean radii of the orbits (that is, the semi-major axes of the orbital ellipses) was merely a matter of arithmetic. Kepler had by then found orbits for all the planets. So the proof was simple - even if Kepler was (it seems) a bit accident-prone in handling the numbers.
Kepler's letters survive in quantity, but all the same he has left no clue how he came to the eventual correct form of the law. It seems likely that he simply tried lots of different formulae, and the one that worked was the one he published. Perhaps the rather long delay before making the revisions indicates that he was racking his brains (unsuccessfully) for an explanation of why the law should take this particular form? It is simple, but not quite simple enough to be explained merely aesthetically.
Proofs and physics
The proofs of Kepler's first two laws are mathematical, but they are dealing with facts that belong to physics. However, this does not rule out Kepler's preferred method of proof, which is exactly that of Euclid: giving definitions and axioms and then proceeding by deduction. All mathematicians of the time, and most philosophers, were agreed that this method was the most reliable one.
However, neat and obviously rigorous methods of deductive proof cannot be applied if one is working with messy numbers derived from observation - or from experiment, for that matter. Even when everyone knows the points one is plotting ought to lie on a straight line, the prudent cheat will give the supposed results an air of reality by putting in some "scatter". On the more serious level: one of the most important things one learns from doing experiments or making observations of one's own is that one usually needs to know rather a lot about the acceptable form of the "answer" in order to deduce it from what one measures. It is because of this that any kind of experimental discovery is usually contested. Sometimes, of course the sceptics are right - as they were about those famous "canals" on Mars.
As Kepler was determined to make the best possible use of the huge number of observations, he used a method that involved repeated trial and error. Historically, this is interesting precisely because we know he otherwise strongly preferred to model himself on Euclid. The method of "try it and check" has in fact got a background in Medieval and Renaissance algebra. But Kepler's methods were not known in astronomy which used geometry, generally regarded (at the time) as intellectually more respectable than algebra. Since Euclid was concerned with geometry, Kepler was inviting direct comparison.
On the other hand, although at the time astronomers were known as "mathematicians", their work did not actually involve proof in quite the same way as Euclid's did. Astronomers were expected to predict, say, positions of the Moon that were then found to agree, or not agree, with observation. Kepler's work is different in that it sets out to find a new geometrical description of the orbit of Mars, and of the structure of the Solar system, and thus gets into proving general laws that are somewhat like theorems.
For a deductive proof of Kepler's laws the world had to wait for Isaac Newton. He took the laws as geometrical facts, and could afford to ignore the numerical vicissitudes that had attended Kepler's proofs.
The proof of the pudding...
With hindsight - which historians all have a lot of - it is clear that Kepler has proved the truth of his three laws, though Newton, who did not actually read Kepler, did remark unkindly that he he knew the orbits were not circular and guessed them to be elliptical. This is not fair. In calculating orbits for the other planets, Kepler did check that the laws applied to them as well.
But the details of Kepler's work on the other planets remained in manuscript, and the mathematics of the New Astronomy was declared extremely difficult by Kepler's contemporaries - a judgement with which it is easy to sympathise. (Newton, who was working much later, had no occasion to go back to Kepler's own books.) What in effect served for proof that Kepler's laws were correct was that the tables he based on them, and on Tycho's observations, proved to be accurate over a long period of time.

Figure 8: Johannes Kepler, Tabulae Rudolphinae, Ulm, 1628, frontispiece. Kepler designed this frontispiece himself. It shows astronomy in the form of a temple, the pillars being the work of past astronomers. Kepler is seen at work in one of the reliefs on the base. Another shows a map of the island of Hveen, in Copenhagen Sound, where Tycho made most of his observations.
Click here for a higher resolution image of the frontispiece.
When Kepler succeeded Tycho as Imperial Mathematician to the Holy Roman Emperor Rudolf II, he took on the task of compiling astronomical tables, which would bear Rudolf's name and thus bring him lasting fame. Kepler's Rudolphine Tables, published in Ulm in 1628, fulfilled this obligation to the letter.
The Rudolphine Tables were the first set of astronomical tables to continue to be reliable for twenty years, for thirty years... As the years mounted up, and Kepler's tables still gave good agreement with observation, their continued accuracy inclined astronomers to accept Kepler's first two laws, and, since these laws both related the planets to the Sun, to share Kepler's belief in the Copernican theory. That wrote QED under something Kepler considered an important truth.
Bibliography
Both of the works discussed here have been published in English translation.
Johannes Kepler, New Astronomy, trans. William H. Donahue, Cambridge: Cambridge University Press, 1992. [Translation of Johannes Kepler, Astronomia nova..., Heidelberg, 1609]
Johannes Kepler, The Harmony of the World, translated into English with an introduction and notes, by E. J. Aiton, A. M. Duncan and J. V. Field, Memoirs of the American Philosophical Society, vol. 209, Philadelphia, 1997. [Translation of Johannes Kepler, Harmonices mundi libri V, Linz, 1619]
On Tycho's instruments, see:
J. V. Field, "What is scientific about a scientific instrument?", Nuncius, III.2, 1988, 3-26.
About the author
Dr J.V. Field, who is a historian of science, has worked on Kepler for many years, but started out as a mathematician, and in the mid 1960s helped to design the optical system of the Anglo-Australian telescope, using Cambridge University's Edsac II and Titan computers.
Dr. Field is an Honorary Visiting Research Fellow in the Department of History of Art, Birkbeck College(University of London).
For further information, see :
- Home Page
- J.V. Field's Home Page
- The da Vinci Society
- The home page of the Leonardo da Vinci Society
- BSHM.
- The British Society for the History of Mathematics
Comments
Anonymous
The area of Kepler's area law for time taken can initially be expressed as the area of a triangle, t=PXBX1/2, but if P and B are replaced by r we have t=rXrX1/2, and if 1/2 becomes a power we have t=rXr^(1/2) which is Kepler's distance law v=r/t=1/r^(1/2) which applies throughout the whole universe.