A symmetry approach to viruses

This model was the inspiration for the work

The BA Festival of Science is one of the UK's biggest celebrations of science. This year York hosted the festival, and attracted around 400 scientists and science communicators from the UK and around the world. While they may not always grab the tabloid headlines, mathematical topics were the focus of a number of the festival highlights.

Dr Reidun Twarock, an EPSRC Advanced Research Fellow and a jointly appointed Reader in the Departments of Mathematics and Biology at the University of York, was the keynote speaker at a mathematical function designed to not only encourage the general public to take up the topic, but to showcase a beautiful mathematical method for understanding and solving a critical modern-day problem.

Dr Twarock's talk, entitled Microworld adventures: a symmetry-approach to viruses, covered the history of how mathematical descriptions of symmetry, group theory and geometry have led to amazing discoveries regarding the shape of viruses. She also talked about how her current research is uncovering new insights into the structures of viruses and the mechanisms underlying virus assembly, and how this potentially opens up novel possibilities for anti-viral drug design. Dr Twarock chatted to Plus and the full interview can be heard on our podcast here.

Viruses, such as hepatitis and HIV, have highly ordered protein shells that are called viral capsids. These protect the viral genomic material, which is either DNA or RNA. "These containers act as Trojan horses, transporting the genomic material inside the cell to hijack the cellular mechanism and produce new viruses. The structures of these protein containers follow symmetry," said Dr Twarock.

The understanding of how capsids are organised is the key to understanding how viruses work and how they can be defeated. The mathematical understanding of viruses started in 1956 when biologists Francis Crick and James Watson observed that the size of the encapsulated genomic material is too small to encode for more than a limited number of distinct capsid proteins. They therefore postulated that small viruses are formed from identical proteins that are arranged according to symmetry. Experiments confirmed that viruses indeed use icosahedral symmetry in the organisation of their capsids, and the overall shape of a small virus resembles an icosahedron, a 20-faced polyhedron (icos derives from the Greek word for "twenty" and hedron comes from the Indo-European word for "face"). Caspar and Klug in 1962 built on this work and explained the organisation of larger viruses based on the concept of quasi-equivalence. They introduced a seminal theory in which they predicted the organisation of the proteins in viral capsids in terms of triangular surface lattices that exhibit the symmetry properties of the icosahedron. These days, this theory is a fundamental tool in virology, used for the classification of viruses and in the reconstruction of their structures from experimental data.

The mathematics behind the Caspar-Klug theory is not difficult. The theory assumes that virus structures can be modelled via triangular lattices that encode schematically the locations of the capsid proteins in the corners of the triangles. "This is recognised as the theory for the description of viral structures," said Dr Twarock.

However, experimental discoveries in 1982 and 1991 found that the cancer-causing group of viruses known as papovaviridae cannot be classified in this way. These viruses are DNA-based and infect the skin and mucous membranes, as well as being associated with cervical cancer.

Papovaviridae have an arrangement of protein clusters that cannot be described via the mathematical techniques of Caspar-Klug theory, and so Dr Twarock developed a new mathematical description using techniques known from the study of quasicrystals — that is, alloys with atomic configurations that are non-periodic but exhibit long-range order, such as Penrose tilings.

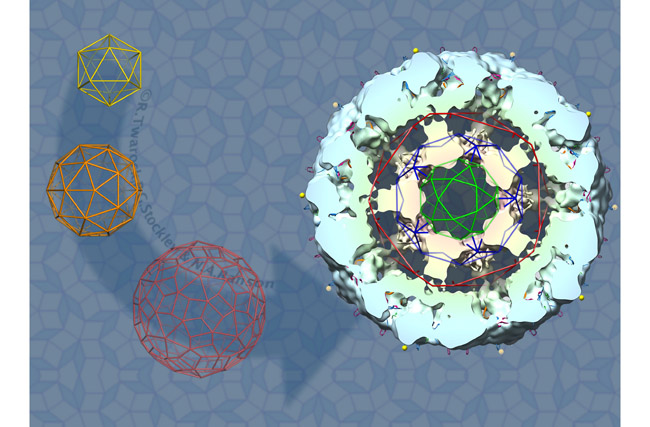
The movement from Crick & Watson, to Caspar & Klug and finally the Twarock model.

Twarock's work has generalised the Caspar-Klug theory to model the surface structures of viruses via tilings that are related to such aperiodic structures in three dimensions. This has resulted in models of viral capsids in terms of more general tessellations, for example, in terms of quadrilaterals. The tiling approach not only encodes the locations, types and relative orientations of the protein clusters in papovaviridae capsids, but it also determines the locations and types of the interactions between them. Such information is important because it elucidates how the different protein clusters in the capsids bond together to form the capsid, and it can hence be used to construct models for the assembly of the viruses from their capsid proteins.

One drawback of Caspar-Klug theory is that information on the three-dimensional structures of viruses in terms of the area occupied by individual capsid proteins and their shapes, the thickness of the protein capsid, and the organisation of the genomic material encapsidated are inaccessible. Twarock's recent work in collaboration with the Astbury Centre for Structural Molecular Biology at the University of Leeds shows that such information can be obtained via an extension of the symmetry principles underlying Caspar-Klug theory and the tiling approach.

"This new approach opens up a lot of novel applications, for example the modelling of virus assembly. We have shown recently that it can be used to incorporate the dependence of capsid assembly on the interaction with the genomic material as a boundary condition into our earlier tile assembly models," said Dr Twarock.

"There is a plethora of questions arising from the new symmetry principle. One of them is viral evolution. We know that capsid proteins in different families of viruses may take on similar overall shapes even though their sequences are distinct, which led to the hypothesis that they may have a common ancestor. However, our analysis shows that this phenomenon may just be an artefact of the limited number of structural blueprints available due to geometric constraints, and hence point to convergent evolution."

The full interview can be heard on our podcast here.